Aplicatii ale teoriei relativitatii restrānse

I.9.1.Studiul miscarii unei particule relativiste sub actiunea unei forte constante

Ne propunem sa gasim relatia dintre forta si acceleratie īn dinamica relativista. Presupunem o forta constanta care actioneaza asupra unei particule cu masa de repaus m₀ si legea fundamentala a dinamicii:

Calculam:

Dar , deci:

Relatia obtinuta ne arata ca īn dinamica relativista, forta si acceleratia nu mai sunt īntotdeauna par 828j96i alele.

Relatia (I.92) poate fi pusa sub alta forma. Consideram al doilea termen din relatia (I.91) si calculam:

dar

Atunci:

, de unde

Cazuri particulare:

Forta este paralela cu viteza:

Cantitatea se numeste masa longitudinala, deci putem scrie:

.

Forta este perpendiculara pe viteza:

Cantitatea se numeste masa transversala, iar īn acest caz

.

Daca consideram din nou legea fundamentala a dinamicii si presupunem ca viteza variaza numai ca modul:

,

integrānd aceasta relatie de la la t (tinānd cont ca iar la ), obtinem:

, de unde

Reprezentānd grafic , obtinem aspectul din fig.I.12.:

Īntr-adevar la īnceputul miscarii (t foarte mic) termenul este neglijabil la numitor si (ca si īn dinamica prerelativista). Daca t este foarte mare, >>1, deci .

I.9.2.Studiul dezintegrarii particulelor relativiste

Consideram o particula cu masa de repaus M₀ care se poate dezintegra spontan (fara interventii exterioare) īn alte doua particule si sa gasim conditiile īn care are loc acest fenomen precum si energiile particulelor rezultate. Consideram cuadrivectorul impuls-energie:

.

Modulul sau patrat:

, deci un invariant relativist.

Pentru particula care se dezintegreaza, īn sistemul centrului sau de masa, impulsul īnainte de dezintegrare este nul, deci invariantul cuadrivectorului impuls-energie se scrie:

.

Cele doua particule provenite din dezintegrare, cu mase de repaus m₀₁ si m₀₂ au impulsurile si iar energiile E₁ si E₂. Īn sistemul centrului de masa , iar invariantul cuadrivectorului impuls-energie este:

Egalānd valorile celor doi invarianti obtinem:

.

Dar

, deci

Cele doua particule rezultate au energii cinetice pozitive, deci M₀>m₀₁+m₀₂.

Īn concluzie, dezintegrarea spontana este posibila numai daca masa de repaus a particulei care se dezintegreaza este mai mare decāt suma maselor de repaus ale produselor de dezintegrare.

Folosind relatiile si si tinānd seama ca , se pot determina cele doua energii.

I.9.3.Defectul de masa

Consideram un nucleu cu masa de repaus M₀, alcatuit din Z protoni si A-Z neutroni. Īn nucleu, neutronii au energii cinetice mari, dar nucleul este stabil din cauza fortelor nucleare. Energia de repaus a nucleului M₀c² va fi suma dintre energiile de repaus ale nucleonilor () si energia de legatura.

Se defineste defectul de masa:

Atunci energia de legatura W devine:

Starile stabile corespund energiilor de legatura negative. Se observa ca daca >0, W este negativa iar nucleul este stabil. Daca īnsa defectul de masa <0, W este pozitiva, deci nucleul este instabil si poate suferi tranzitii spontane.

I.10.Exercitii si probleme

1) Doua mobile M₁ si M₂ au fata de un referential inertial (R) ecuatiile de miscare

M₁: x=0;  y=ut+a; z=0;

M₂: x=b;  y=ut+a; z=0; (unde a este o constanta)

a)  Sa se scrie ecuatiile de miscare ale celor doua mobile īn raport cu referentialul (R') aflat īn miscare cu viteza v fata de (R) de-a lungul axei O'x' comuna cu Ox;

b)  Sa se calculeze, īn fiecare referential, momentele la care mobilele traverseaza planul xOz si sa se interpreteze rezultatul.

Rezolvare:

a.         Pentru M₁: (1)

deci (2)

(3)

Pentru M₂:

sau de unde

(4)

īnlocuind din (4) obtinem

(5)

=z=0

b)        Traversarea planului xOz presupune y=0.

Pentru observatorul din referentialul (R), momentele traversarii sunt aceleasi:

t₁=t₂=-

deci evenimentele sunt simultane.

Pentru un observator din () traversarea (y=0) va avea loc la momentele:

(din (2))

si (din (5))

deci evenimentele nu mai sunt simultane.

2) O racheta cu masa de repaus m₀=3t se deplaseaza de-a lungul axei Ox cu viteza c fata de Pamānt.

O a doua racheta se deplaseaza paralel cu prima, dupa legea fata de Pamānt. Sa se determine:

a)  ecuatia de miscare a celei de a doua rachete fata de prima;

b)  masa de repaus a celei de a doua rachete astfel īncāt ambele sa posede aceeasi energie cinetica fata de Pamānt.

Rezolvare:

a)   viteza celei de a doua rachete fata de Pamānt este:

.

Consideram un sistem de referinta () legat de prima racheta, deci care se misca fata de (R) (Pamāntul) cu v=u_1x. Atunci viteza celei de-a doua rachete fata de () va fi:

Legea de miscare īn raport cu ():

b) din conditia data īn enunt, notānd M₀ masa de repaus a celei de a doua rachete

de unde , īnlocuind si c ,obtinem tone.

Doua particule se deplaseaza fata de un referential (R) dupa doua directii ce fac un unghi drept īntre ele, cu vitezele u₁, si, respectiv, u₂. Sa se calculeze viteza particulei a doua īn raport cu prima.

Rezolvare:

u_2x=0; u_2y=u₂

Consideram un referential () legat de prima particula, deci care se misca cu v=u₁ fata de (R) (v//Ox).

Atunci:

Īn cazul nerelativist

4) Doua evenimente se petrec īn punctele A si B separate prin distanta l=1m si sunt percepute simultan de catre un observator īn repaus fata de aceste puncte. stiind ca un observator care se misca cu viteza fata de primul, de-a lungul segmentului AB le percepe ca petrecāndu-se īn punctele si separate de =2m, care este intervalul de timp la care se succed cele doua evenimente pentru observatorul īn miscare?

Rezolvare:

Notam x₁, x₂ abscisele punctelor A si B masurate de observatorul fix si abscisele acestor puncte masurate de observatorul mobil la momentele respectiv cānd el percepe evenimentele.

de unde

.

Avem de asemenea:

; , de unde

sau

.

De aici

si

5) Densitatea unui corp īn repaus este . Sa se determine viteza referentialului īn care densitatea masurata este cu f = 20% mai mare decāt .

Rezolvare:

Densitatea corpului īn repaus

Pentru un corp īn miscare cu viteza v, 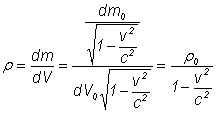, deci depinde de patratul vitezei. Aceasta densitate ar masura-o si un observator care se misca fata de corp cu aceeasi viteza.

de unde

6) Energia mezonilor rapizi din razele cosmice este E=3000MeV iar energia lor de repaus este Ce distanta pot strabate acesti mezoni prin atmosfera īn timpul lor de viata, daca īn sistemul de referinta propriu au timpul de viata t =2,2 10^-6s?

Rezolvare:

Energia totala de unde rezulta

si

Spatiul parcurs īn atmosfera este S = vt unde t este timpul de viata īntr-un referential legat de Pamānt.

.

7) Sa se calculeze cu ce viteza trebuie sa se apropie un automobil de un semafor pentru a ,,vedea'' culoarea rosie drept verde. Se dau l_verde=550nm, l_rosu=650nm.

Rezolvare:

Este vorba de un efect Doppler-Fizeau (relativist) longitudinal. Īn acest caz frecventa sursei este n_rosu n frecventa receptata este n_verde n iar observatorul se apropie de sursa. Conform relatiei (I.45)

unde v--> -v (apropiere) deci .

Dar , deci , de unde

.(!?)

8) O particula cu masa relativista m se deplaseaza cu viteza constanta u fata de un referential (R). Sa se calculeze masa relativista m' a aceleiasi particule masurata de un observator solidar cu un referential (R') care se deplaseaza uniform cu viteza de-a lungul axei Ox fata de (R).

Rezolvare:

Notam m₀ masa de repaus a particulei.

, unde u' este viteza particulei fata de (R').

sau

.

Atunci:

deci

9) O particula cu masa de repaus M₀ ,necunoscuta, se afla īn repaus si se dezintegreaza īn alte doua particule cu masele de repaus m₀₁ si m₀₂ (masurate). Cunoscānd energia cinetica a primei particule E_c1 sa se calculeze:

a.  energiile totale E₁ si E₂

b.  masa de repaus M₀ a particulei initiale.

Rezolvare:

a. Energiile totale sunt : E₁=m₀₁c²+E_c1; E₂=m₀₂c²+E_c2

Īntrucāt particula primara era īn repaus iar produsele de dezintegrare au impulsurile si , din legea conservarii impulsului:, de unde

Dar din relatia relativista energie-impuls avem:

,

care prin scadere duc la

.

Ţinānd seama ca obtinem

b. Conservarea energiei īn procesul de dezintegrare se scrie:

10) Un atom excitat īn repaus emite prin dezexcitare un foton cu frecventa n . Daca atomul se afla īn miscare, calculati frecventa radiatiei emise n si diferenta frecventelor Dn n n (deplasarea Doppler) (folositi legea de conservare a energiei si a impulsului).

Rezolvare:

Notam m₀ - masa de repaus a atomului īnainte de emisia fotonului. Dupa emisie el va avea masa de repaus m₀', astfel ca:

m₀-m₀' c²=hn

unde n este frecventa fotonului emis.

Presupunem acum ca īnainte de emisie atomul se misca cu viteza v si emite o radiatie cu frecventa n dupa o directie care face un unghi q cu directia initiala a miscarii, iar dupa emisie atomul se deplaseaza pe o directie care face unghiul a cu cea initiala (vezi figura I.14).

Legea conservarii impulsului (pe cele doua directii Ox si Oy) se va scrie:

(2)

(3)

Legea conservarii energiei este:

(4)

Separānd īn relatiile (2) si (3) termenii care contin a, ridicāndu-le la patrat si adunāndu-le se obtine:

(5)

Ridicānd relatia (4) la patrat obtinem:

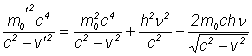(6)

Scazānd ecuatia (5) din ecuatia (6) rezulta:

(7)

Dar din (1)

care īnlocuita īn (7) duce la :

Neglijānd ultimul termen obtinem:

Pentru emisia fotonilor de catre probe la temperaturi īnalte, viteza agitatiei termice poate fi de ordinul . Īn acest caz, dezvoltānd īn serie, retinānd doar primii doi termeni si scriind variatia relativa a frecventei obtinem:

sau . (am notat deplasarea frecventei fotonului emis datorita efectului Doppler).

11) Ce viteza va avea un electron accelerat īntr-o diferenta de potential U=10⁵V?

Rezolvare:

Teorema variatiei energiei cinetice DE_c=L se va scrie īn cazul relativist:

c²(m-m₀)=eU sau

(1)

Dezvoltānd īn serie si retinānd primii trei termeni avem:

sau (2)

Se obtine ecuatia bipatrata 3m₀v⁴+4m₀c²v²-8eUc²=0, din care v=0,56c.

Observatie: daca v/c 0 din (2) se obtine m₀v²/2=eU adica tocmai relatia din mecanica prerelativista.

Facānd calculul exact, dupa relatia (1) se obtine v=0,53c.

12) O particula cu sarcina q si masa de repaus m₀ se deplaseaza cu viteza de-a lungul axei Ox a unui referential (R). De-a lungul axei Oy actioneaza un cāmp magnetic cu inductia . Calculati raza traiectoriei particulei si energia sa totala.

Rezolvare:

Impulsul particulei fata de referentialul (R) este:

Forta Lorentz

este perpendiculara pe deci si pe ; rezulta. Dar , deci , adica īn cāmp magnetic modulul impulsului particulei nu se modifica; traiectoria sa ramāne īn planul xOz iar forta Lorentz va fi forta centrala (centripeta).

deci .

Energia totala

.

Bibliografie

Capitolul I

Ion M. Popescu "Fizica (I)" - Editura Didactica si Pedagogica, Bucuresti, 1982.

G.C.Moisil, E.Curatu "Optica - Teorie si aplicatii" Editura Tehnica, Bucuresti, 1986.

C.Motoc "Fizica" vol I - Editura All, Bucuresti, 1994.

N.Barbulescu "Bazele fizice ale relativitatii restrānse" Editura stiintifica si Enciclopedica, Bucuresti, 1979.

Al.Stoenescu "Introducere īn teoria relativitatii" Editura Tehnica, Bucuresti, 1964.

G.Cone, C.Negutu "Mecanica punctului material si a solidului rigid. Teoria relativitatii restrānse" (probleme cu rezolvari), Matrix Rom, Bucuresti, 2000.

st. Tudorache, M.Stan "Probleme rezolvate de fizica", vol.I, Litografia I.B.P., Bucuresti ,1981.