Bariera de potential
Particula se misca in sensul pozitiv al axei 
si evergia ei
potentiala are expresia:
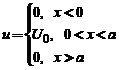
.Consideram cazul in care energia ei este mai mica decat
inaltimea 
a barierei de
potential 
In regiunea 
si 
ecuatia
Schrodinger atemporala se scrie:
Solutia ei este: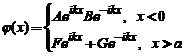
, conducand la undele plane:
.
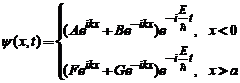Deoarece unda plana regresiva 
nu are sens fizic, o
vom elimina 
. In regiunea 
ecuatia
Schrodinger atemporala are forma:
avand solutia: 
. Reunind toate expresiile putem scrie functia de
unda astfel:
Punand conditia de continuitate a functie de unda
si a deviatiei sale in 
si 
si rezultand
sistemul de ecuatii astfel obtinut, vom putea calcula 
: coeficientii de reflexie si respectiv transmisie
ai barierei de potential:
inseamna ca
particula cuantica poate penetra o bariera de potential chiar
daca 
, ceea ce o particula clasica nu poate. E ca
si cum, pentru un interval scurt de timp 
, particula ‘‘imprumut’’ de la ‘‘spatiu gol’’ sau
‘‘vidul cuantic’’ energia necesara depasirii barierei. Este ceea
ce numim « efectul tunel » sau
« « tunelarea barierei ».
Un
bun exemplu de efect tunel este oferit de dezintegrarea 
a nucleelor
radioactive. Se imagineaza particula 
inchisa in modul
radioactiv de bariera de potential electrostatic creata de celelalte
particule (protonii) din nucleu :
raza nucleului.
Cunoscand dimensiunile nucleului si energia particulelor emise de nucleul
radioactiv putem calcula probabilitatea de dezintegrare si deci timpul de
injumatatire. Predictiile, bazate pe calcule ale lui 
asemanatoare
cu cele prezentate pana acum, au o concordanta buna cu
datele experimentale.
|
