CATEGORII DE MASURARI - Masurari indirecte, statice, dinamice

CATEGORII DE MaSURaRI

Metodele de masurare definesc in buna masura si categoriile de masurari ce pot fi efectuate cu ele. Exista insa si alte aspecte ale procesului de masurare care diversifica si caracterizeaza anumite categorii de masurari si anume:

- modul (direct sau indirect) de obtinere a rezultatului masurarii, care diferentiaza masurarile in urmatoarele categorii:

- masurari directe;

- masurari indirecte;

- regimul de variatie al marimii de masurat in timpul masurarii dupa care se definesc urmatoarele trei categorii:

- masurari statice;

- masurari dinamice;

- masurari statistice;

- forma in care se obtine si se prezinta rezultatul masurarii, dupa care deosebim categoriile:

- masurari analogice;

- masurari numerice;

- specificul domeniului de aplicatie care delimiteaza masurarile in:

- masurari industriale;

- masurari si verific&# 323b19d 259;ri de laborator.

1. Masurari directe

Masurarile directe sunt acele masurari ale unei singure proprietati care se efectueaza cu ajutorul unor sisteme relativ simple in care marimea de masurat este perceputa, masurata si vizualizata pe baza compararii cu un etalon apartinand aceleiasi clase.

La scara industriala masurarile directe se fac in cadrul unui sistem ca cel din figura 1.7, din care fac parte, de regula, urmatoarele elemente componente:

senzorul sau traductorul;

aparatul de masurare si vizualizare, AMV;

elemente de convertire si/sau adaptare, ECA, daca este nevoie.

Senzorul S sau cum se mai numeste, traductorul primar TP, este elementul primar care transpune valoarea marimii masurate, x, pe un semnal purtator de informatie, y. Acest semnal y se aplica la intrarea aparatului de masurare si vizualizare, AMV, direct sau dupa o prealabila convertire si/sau adaptare, daca este necesara.

Convertirea este operatia de transpunere a marimii x de pe un semnal purtator de informatie y pe alt semnal purtator de informatie y_T, de alta natura. Aceasta operatie este necesara atunci cand natura semnalului y nu coincide cu natura marimii de intrare a AMV.

De exemplu, daca dorim sa masuram presiunea cu un manometru cu tub Burdon si sa vizualizam rezultatul masurarii cu un AMV cu marimea de intrare curent electric unificat I = 2 - 10 mA, atunci este nevoie de un convertor deplasare curent care sa transpuna valoarea presiunii de pe semnalul deplasare dat de senzor pe semnalul curent acceptat de AMV.

Ansamblul senzor convertor este numit traductorul marimii masurate de AMV si poate fi realizat intr-un singur bloc.

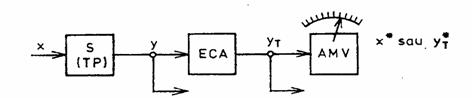
Fig.1.7. Structura unui sistem pentru masurare directa.

In cadrul conexiunii traductorului cu aparatul de masurare, ca si in cazul altor conexiuni, o atentie deosebita trebuie acordata adaptarii semnalului ce se transmite de la un element la altul pentru a asigura compatibilitatea conexiunii.

Adaptarea inseamna modificarea semnalului dat de un element (emitent) astfel incat sa se incadreze intre limitele prescrise ale semnalului admis de intrarea elementului urmator (receptor). Semnalul elementului emitent trebuie deci sa fie de aceeasi natura cu semnalul acceptat de intrarea elementului receptor si sa aiba aceleasi limite de variatie.

Daca limitele de variatie ale semnalului elementului emitent sunt mai largi decat ale semnalului admis de elementul receptor, acesta nu va putea receptiona intreaga gama de valori a marimii masurate; in celalalt caz, cand limitele de variatie ale semnalului elementului emitent sunt mai inguste decat cele ale semnalului acceptat de elementul receptor, acesta nu va fi folosit rational, deoarece ar lucra numai pe o anumita zona din domeniul lui de masurare.

Revenind la schema din figura 1.7 putem arata ca in procesul de masurare au loc urmatoarele operatii si transformari:

1. Transpunerea valorii marimii de masurat x pe un semnal purtator de informatie y, operatie care are loc in senzor. In cazul transpunerii printr-o singura transformare avem:

, (1.28)

pe cand in cazul transpunerii prin mai multe transformari avem:

(1.29)

2. Masurarea semnalului y sau y_T cu ajutorul AMV. Rezultatul masurarii poate fi dat in valori ale acestui semnal, ceea ce este mai putin convenabil pentru utilizatorul AMV, sau in valori ale marimii transpuse pe semnalul y sau y_T ceea ce este convenabil pentru utilizator. In primul caz scala aparatului urmeaza a fi gradata in unitati de masura pentru semnalul y sau y_T , pe cand in al doilea caz scala se gradeaza in unitati de masura a marimii masurate si transpuse pe semnalul y. In al doilea caz este necesara si operatia de la punctul 3.

3. Transpunerea valorilor masurate ale lui y sau y_T in valori exprimate in unitati de masura ale lui x se face o singura data in timpul operatiei de gradare (etalonare) a scalei AMV. Aceasta transpunere se face pe baza relatiilor de transformare inversa:

(1.30)

unde j este functia de transformare inversa.

Dupa cum se vede din figura 1.7 semnalul y obtinut de la senzor, sau semnalul y_T, obtinut de la blocul traductor, poate fi folosit nu numai in cadrul sistemului de masurare, ci si in cadrul altor sisteme, ca de pilda in sisteme de semnalizare, in sisteme de reglare, in sisteme de protectie.

Masurari indirecte

Masurarile indirecte se aplica la determinarea unor marimi care se deduc prin calcule pe baza unor relatii dintre aceste marimi si doua sau mai multe marimi masurabile direct. Prin urmare, o masurare indirecta consta in doua sau mai multe masurari directe urmate de operatii de calcul si vizualizare.

Dupa forma relatiei de dependenta deosebim:

metode indirecte bazate pe relatii explicite;

metode indirecte bazate pe relatii implicite.

Metodele bazate pe relatii explicite sunt mai uzuale si mai simple, deoarece pot fi aplicate in cadrul unor aparate dotate cu mai multi senzori, precum si cu elemente de calcul specializat incorporate in aparatul respectiv. Sub aspect matematic se pune deci problema determinarii unei marimi y pe baza unei dependente explicite sub forma:

(1.31)

unde x₁, x₂,, x_n sunt marimi masurabile direct.

Marimea y transpusa pe un semnal purtator de informatie urmeaza a fi masurata si vizualizata asa cum se sugereaza in figura 1.8.

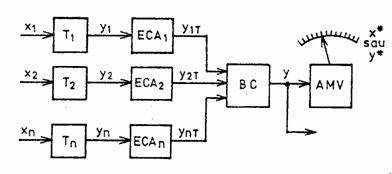
Fig.1.8. Sistem pentru masurare indirecta.

Elementele de convertire si adaptare ECA₁ - ECA_n si blocul de calcul BC determina marimea y care este apoi masurata si vizualizata cu un aparat corespunzator. Prin urmare, in structura unui aparat (sistem) pentru masurari indirecte intra, pe langa elementele specifice aparatelor de masurari directe, un bloc de calcul BC. Elementele de convertire si adaptare ECA pot face parte din structura traductoarelor pentru marimile x₁ , , x_n sau pot face parte din structura blocului de calcul BC.

Ca exemplu de aparat pentru masurari indirecte poate fi dat wattmetrul cu care se determina puterea electrica pe baza relatiei P = UI. Un astfel de aparat are in componenta lui un senzor (traductor) de tensiune, un senzor (traductor) de curent, un dispozitiv electrodinamic care genereaza un cuplu activ proportional cu produsul UI (elementul de calcul) si un dispozitiv de echilibrare si vizualizare similar cu cele din cadrul aparatelor pentru masurari directe.

Din cauza posibilitatilor de cumulare a erorilor produse de blocul de calcul precizia masurarilor indirecte este in principiu mai redusa decat precizia masurarilor directe.

Masurari statice

Masurarile statice se caracterizeaza prin aceea ca pe toata durata masurarii, marimea de masurat se considera a fi practic constanta. In astfel de cazuri, durata regimului static trebuie sa depaseasca durata masurarii, adica tranzitia de la o stare de echilibru corespunzatoare valorii nule a marimii de masurat la o stare de echilibru corespunzatoare valorii curente a acesteia. In aceste conditii valoarea marimii masurate se obtine direct fara a fi nevoie de elemente de memorare a acesteia.

Desi nu se poate vorbi de marimi invariabile in timp in mod absolut, mai ales in timp mai indelungat, masurarile statice sau cele cvasistatice sunt cele mai uzuale deoarece un mare numar de marimi fizice evolueaza relativ lent, iar variatia lor pe timpul masurarii poate fi neglijata.

Masurari dinamice

Masurarile dinamice se caracterizeaza prin aceea ca se refera la marimi care au variatii rapide in timp si care variaza deci in timpul procesului de masurare. In astfel de cazuri masurarea se realizeaza cu ajutorul unor aparate fara inertie sau cu inertie mica sau, in cazul unor variatii foarte rapide, se realizeaza cu ajutorul unor elemente de sesizare, de memorare si de vizualizare specifice care au rolul de a retine valorile marimii masurate din anumite momente de timp, pe anumite intervale de timp, si de a reda aceste valori fie direct, ca valori momentane, fie sub forma unui grafic.

Masurarile dinamice prezinta unele particularitati ce depind de caracterul evolutiei in timp a marimii de masurat. Astfel, dupa acest criteriu, marimile pot fi deterministe sau aleatoare, iar marimile deterministe pot fi periodice sau neperiodice.

Marimile deterministe se caracterizeaza prin aceea ca evolutia lor in timp este previzibila si deci ele se pot exprima printr-o functie de timp continua sau discontinua care pune in evidenta valoarea in orice moment de timp.

Marimile aleatoare au o evolutie neprevizibila in sensul ca valorile pe care le capata la diverse momente de timp sunt absolut intamplatoare. Ele nu pot fi caracterizate decat in sens probabilistic cu ajutorul metodelor statistice.

Marimile deterministe periodice au proprietatea ca valorile pe care le iau la anumite momente de timp se repeta, adica pot fi descrise de o functie de forma:

(1.32)

unde T este perioada de repetare.

Orice marime periodica x(t) poate fi considerata ca o suma alcatuita dintr-o componenta constanta, definita ca o valoare medie

(1.33)

si o componenta alternativa, care este o suma de componente alternative cu valoarea medie nula exprimata printr-o serie Fourier sub forma

(1.34)

unde w p/T reprezinta pulsatia si j_k faza. Termenul sumei pentru k = 1 se numeste fundamentala iar ceilalti termeni sunt denumiti armonice. Valoarea medie poate fi inclusa in suma (1.34) daca in loc de k = 1 se adopta k = 0.

Marimile periodice pot fi deci complet determinate daca se cunosc valoarea medie, perioada, numarul si fazele armonicelor. Descrierea acestor marimi prin relatii de tipul (1.32)…(1.34) presupune integrarea tuturor valorilor pe care le capata marimea respectiva in decurs de o perioada. Valorile armonicelor si ale fazelor se calculeaza cu formulele urmatoare:

(1.35)

(1.36)

(1.37)

. (1.38)

Unii parametri ai marimilor periodice care raman constanti pe o anumita durata pot fi determinati prin metode corespunzatoare masurarilor statice. De exemplu, valoarea medie sau valoarea eficace ale tensiunii si curentului electric alternativ, ca si frecventa acestuia pot fi masurate cu aparate pentru masurari statice.

In fine, in cazul reprezentarii marimilor perfect sinusoidale este suficient sa se precizeze valoarea maxima sau valoarea eficace si perioada. Precizarea fazei este necesara numai in cazurile in care intervin raporturi cu alte marimi.

Masurari statistice

Masurarile statistice se fac asupra marimilor aleatoare, adica asupra acelor marimi care au o evolutie intamplatoare si deci nu pot fi descrise de functii deterministe, ci cu functii statistice.

Functiile ale caror valori reprezinta marimi aleatoare pentru orice evolutie a variabilei independente se numesc functii aleatoare, iar daca variabila independenta este timpul, functia respectiva reprezinta ceea ce se numeste un proces aleator.

Totalitatea valorilor obtinute printr-un experiment asupra unui proces aleator constituie ceea ce se numeste o realizare x_i(t) a acestuia iar prin repetarea experimentelor se obtine un ansamblu de realizari sau esantioane care descriu procesul aleator in cauza (fig.1.9).

La un anumit moment de timp t = t_k un proces aleator x(t) este caracterizat de un ansamblu de valori x_i(t), i = 1,2 ,, n, ceea ce inseamna ca procesul aleator este descris de o functie de doua variabile: timpul t si multimea celor n esantioane intre care nu se pot stabili relatii de interdependenta.

Fig.1.9. Un set de realizari ale unui proces aleator.

In aceste circumstante nu se pot stabili relatii matematice care sa descrie evolutia in timp a procesului aleator, ca in cazul proceselor deterministe. Masurarea uneia sau alteia dintre valorile obtinute in urma realizarii a unui proces aleator nu prezinta interes daca acea valoare nu este asociata cu probabilitatea de aparitie a lui.

Determinarea unor caracteristici generale ale proceselor aleatoare se poate face deci numai in sens probabilistic, luand in considerare toate valorile cuprinse in ansamblul de esantioane din cadrul procesului aleator considerat.

Prin urmare, evaluarea acestor caracteristici se poate face doar pe baza unui mare numar de masurari statistice. Cele mai importante caracteristici probabilistice ale unui proces aleator continuu sunt: functia de repartitie de probabilitate, functia de densitate de repartitie, momentele si dispersia.

Masurari analogice

Masurarile analogice se caracterizeaza prin aceea ca atat marimea de masurat cat si rezultatul masurarii se manifesta si se exprima prin relatii continui de forma

, (1.39)

dependenta dintre marimea de masurat x si rezultatul masurarii y putand fi liniara sau neliniara. Dintr-o astfel de relatie se observa ca unei evolutii continue a marimii de masurat ii corespunde o evolutie tot continua a rezultatului masurarii existand astfel o analogie intre evolutiile celor doua marimi. Aparatele cu care se realizeaza astfel de masurari se numesc aparate de tip analogic iar elementele lor componente se numesc elemente de tip analogic.

Masurarile analogice au fost primele utilizate si continua sa fie folosite cu o pondere importanta si in prezent. Acestea se realizeaza cu ajutorul unor aparate de uz general la care marimea de iesire este deplasarea (pozitia) unui ac indicator sau a unui inscriptor in fata unei scari gradate, deplasare care urmareste continuu evolutia marimii de masurat.

Transpunerea deplasarii acului indicator intr-un numar care sa reprezinte marimea masurata se face printr-o operatie de 'citire' efectuata de operator-utilizator pe baza pozitiei acului fata de gradatiile scarii aparatului. Datorita deplasarii continui a acului, aparatul de masurat poate exprima orice valoare din domeniul sau de masurare. Practic insa rezultatul masurarii se exprima printr-un numar finit relativ mic de cifre semnificative, de obicei doua sau trei.

Exprimarea printr-un numar finit de cifre semnificative a rezultatului masurarii inseamna de fapt discretizarea marimii de masurat continui, iar aceasta discretizare o face operatorul utilizator al aparatului de masurat prin operatia de 'citire' a rezultatului masurarii.

Asadar, in cazul masurarilor analogice, transpunerea rezultatului masurarii din forma analogica in forma numerica o face operatorul uman. Din nefericire aceasta transpunere se face cu oarecare incetineala si cu oarecare subiectivitate in functie de acuitatea simturilor umane, ceea ce face posibila introducerea de erori de apreciere.

Masurari numerice

Masurarile numerice se caracterizeaza prin aceea ca furnizeaza rezultatul masurarii direct sub forma numerica cu ajutorul unor dispozitive de afisare sau inscriere cu cifre. In acest caz nu mai este necesara aprecierea prin citire a rezultatului masurarii de catre utilizator si se elimina astfel dezavantajele legate de subiectivitatea citirii rezultatului masurarii. Se maresc precizia, reproductivitatea, viteza de masurare s.a.

La baza masurarilor numerice stau operatiile de esantionare, cuantificare si codificare.

Esantionarea consta in prelevarea dintr-un semnal continuu a unui esantion sau a unui tren de esantioane extrase la diverse momente de timp, la intervale egale sau cand semnalul continuu trece prin anumite valori.

Cuantificarea este operatia prin care o marime esantionata este aproximata printr-un numar finit de cuante. Fiecare cuanta reprezinta o anumita valoare ce se exprima in unitatile de masura adoptate, in submultiplii sau multiplii acestora, iar valoarea marimii masurate se exprima printr-un numar intreg de cuante; se admite astfel si aici un anumit grad de aproximare prin neglijarea fractiunilor de cuanta. Evident, cu cat cuantele sunt mai mici cu atat aproximarea este mai buna.

Cuantificarea inseamna deci discretizarea marimii de masurat, printr-un numar finit de cuante. Trecerea de la o cuanta la alta imediat vecina se face prin salt asa cum se arata in figura 1.10, unde se prezinta caracteristica de intrare iesire a unui aparat de masurare numeric. Operatia de masurare cu aparate numerice consta deci in determinarea numarului de cuante ca echivalent al marimii masurate in momentul esantionarii si exprimarea acestei marimi intr-un anumit sistem de numeratie, de obicei in sistem zecimal sau binar.

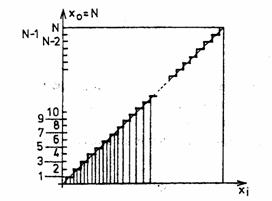
Fig.1.10. Caracteristica intrare-iesire a unui aparat numeric.

Exprimarea rezultatului masurarii intr-un sistem de numeratie (cod numeric) este in fond o operatie de codificare, intrucat prin ea se face atribuirea de numere marimilor cuantificate. Aceasta operatie se face cu ajutorul unor dispozitive adecvate, care in functie de valoarea marimii masurate genereaza numere pe care le afiseaza sau le inscrie.

Masurarile numerice au o serie de avantaje dintre care mentionam:

prezinta rezultatul masurarii direct sub forma numerica, eliminand astfel subiectivitatea si erorile de citire;

operand cu marimi discrete, acestea pot fi mai usor transmise, prelucrate si memorate decat marimile continui si au imunitate mai mare fata de factorii perturbatori;

printr-o cuantificare mai fina se pot realiza o rezolutie si o precizie oricat de bune, rezolutia nemaifiind conditionata de dimensiunile scalei aparatului;

aparatele de masurare numerice pot fi conectate in sisteme moderne de supraveghere, de control si automatizare cu procesoare (calculatoare) numerice.

Masurari industriale

Masurarile industriale au ca obiect principal masurarea variabilelor unui proces in desfasurare cu scopul de a determina starea in care acesta se afla.

Masurarile industriale se efectueza in instalatii care functioneaza in conditiile oferite de mediul unde acestea sunt amplasate. Adesea, aceste conditii sunt dificile si schimbatoare. De aceea, pentru efectuarea unor astfel de masurari se folosesc aparate mai putin sensibile si precise, dar fiabile, robuste si astfel protejate incat sa poata functiona corect in mediile industriale ostile, cu variatii mari de temperatura, de presiune, de umiditate, cu vibratii, cu agenti agresivi s.a.

Aparatele de masurat industriale sunt de obicei aparate stabile montate permanent in instalatie si masoara in mod continuu marimile aplicate la intrare. In general, la masurarile industriale nu se efectueaza corectii ulterioare ale rezultatului masurarii pe baza calculului erorilor de masurare. Se prefera insa folosirea aparatelor de masurare dotate cu dispozitive de corectie automata a erorilor de masurare.

Masurari de laborator

Masurarile de laborator se caracterizeaza prin aceea ca se efectueaza in conditii adecvate, cu mijloace pregatite in mod corespunzator si de catre personal specializat, ceea ce garanteaza o inalta precizie de masurare.

Se pot folosi aparate de masurare de mare sensibilitate si precizie, stabile sau portabile, in conditii adecvate de mediu. La nevoie se pot face masurari repetate, precum si calculul si corectia erorilor de masurare comise. Se adopta de preferinta metode de comparare utilizand etaloane de comparatie de mare precizie, care se pastreaza, de asemenea, in conditii adecvate.

Masurarile de laborator se efectueaza indeosebi cu scopuri de cercetare stiintifica, de verificare metrologica a aparatelor de masurare, pentru realizarea si transmiterea unor unitati de masura, pentru etalonarea si verificarea aparatelor de masurare s.a.