Campul magnetic

Campul magnetic

Un mare numar de experiente arata ca intre circuite parcurse de curent electric se exercita interactiuni a caror marime si sens sunt determinate, pentru aceleasi circuite, de intensitatea si sensul curentilor care le strabat.

Astfel,

- intre doua conductoare rectilinii, parcurse de curenti stationari in acelasi sens, se exercita forta de atractie, iar daca sensurile curentilor sunt opuse, fortele sunt de respingere;

- o spira parcursa de curent electric este supusa unui cuplu de forte daca se afla in preajma unui alt conductor parcurs de curent.

Interactiunile magnetice se manifesta si intre circuite parcurse de curent si corpuri magnetizate, ca de exemplu, intre un conductor parcurs de curent si un ac magnetic, care are tendinta de a se orienta perpendicular pe directia curentului din conductor (Oersted, 1820) sau, de asemenea, intre doua corpuri magnetizate.

Alte experiente care pun in evidenta interactiunile magnetice sunt cele in care fasciculele de particule incarcate cu sarcina electrica sunt deviate in apropierea unor circuite parcurse de curent sau in apropierea unor magneti permanenti. Toate aceste experiente demonstreaza existenta fortelor de interactiune intre 838d35i sarcinile electrice aflate in miscare. Aceasta afirmatie este valabila si pentru corpurile magnetizate, nestrabatute de curenti macroscopici, dar care la scara atomica prezinta curenti electronici.

Asa cum intre sarcinile electrice in repaus se exercitau forte electrice, intre sarcinile electrice aflate in miscare se exercita forte magnetice. Pentru a intelege transmiterea interactiunilor magnetice trebuie sa admitem ca

Experientele arata ca asupra sarcinii q care se deplaseaza cu viteza in camp magnetic actioneaza forta:

(15.1)

numit forta Lorentz. Marimea vectoriala definita de relatia (15.1) poarta numele de inductie magnetica.

15.1.Vectorii si

Vom stabili in continuare o relatie care sa exprime direct legatura intre campul magnetic si curentul electric care il genereaza.

Consideram cazul curentilor stationari a caror densitate de curent satisface ecuatia:

div (15.2)

NOTA:

Pentru explicatii suplimentare privind operatorii vectoriali (divergenta, gradient, rotational) se va consulta anexa II.

Din analiza vectoriala stim ca divergenta rotorului unui camp de vectori este egala cu zero:

div (15.3)

Tinand cont de aceasta relatie, densitatea de curent poate fi exprimata ca rotorul unui camp de vectori

(15.4)

Marimea vectoriala definita prin relatia (15.4) (pentru cazul curentilor stationari) poarta numele de intensitate a campului magnetic.

Nota.Campul magnetic se masoara in amperi metru (A/m).Inductia magnetica se masoara in tesla (T).

Experientele arata ca exista o proportionalitate intre intensitatea curentului electric si inductia campului magnetic creat de acel curent. Tinand cont de aceasta constatare si de (15.4) se poate scrie o relatie care sa lege vectorii si , de forma:

(15.5)

Factorul poarta numele de permeabilitate magnetica a vidului si are valoarea

15.2 . Legea lui Ampére

Sa revenim acum asupra caracterului vectorial al intensitatii campului magnetic si sa calculam circulatia acestui vector de-a lungul unei curbe inchise ce limiteaza o suprafata S strabatuta de fluxul liniilor de curent (fig.15.1) in regim stationar. Fluxul

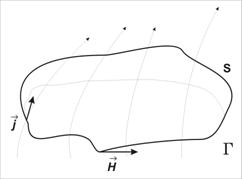
Fig.15.1.Fluxul densitatiide curent

vectorului densitate de curent prin suprafata S este, conform relatiei (15.4):

(15.6)

Membrul stang reprezinta intensitatea curentului I . Transformand membrul drept cu ajutorul teoremei lui Stokes rezulta ca:

(15.7)

Relatiile (15.4) si (15.7) exprima legea lui Ampére sub forma diferentiala respectiv sub forma integrala. In functie de vectorul inductia magnetica cele doua expresii se scriu astfel:

rot (15.8)

(15.9)

Daca ne referim la un conductor strabatut de un curent I, este evident ca circulatia lui de-a lungul oricarei curbe ce contine conductorul va fi egala cu I si va fi nula atunci cand curba inchisa nu contine conductorul.

Cand conturul de integrare inchide mai multi curenti, expresia curentului I din relatia (15.9) se inlocuieste cu curentul total dat de suma algebrica ce tine seama de sensul curentilor.

Legea lui Ampére reprezinta o relatie de legatura intre campul magnetic si sursele care-i dau nastere, adica de curentii electrici de conductie. Apare astfel posibilitatea de a se calcula campul magnetic atunci cand se cunoaste intensitatea curentului.

Aplicarea legii lui Ampére la calculul campului magnetic este avantajoasa atunci cand conturul de integrare poate fi astfel ales incat inductia magnetica sa aiba aceeasi valoare in toate punctele.

15.3.Aplicatie. Campul magnetic al unui solenoid

Un exemplu de aplicare a legii lui Ampére este calculul campului magnetic in interiorul unui solenoid.

Solenoidul este un conductor avand forma unei spirale cilindrice, diametrul spirelor fiind mai mic ca lungimea cilindrului. in figura 15.2 este prezentata sectiunea axiala a unui solenoid, avand n spire pe unitatea de lungime. Fie I intensitatea curentului care strabate spirele solenoidului.

Fig.15.2. Calculul campului magnetic printr-un solenoid

Pentru a calcula campul magnetic in interiorul unui solenoid, folosind legea lui Ampére, trebuie sa tinem cont de doua considerente.

- in primul rand, daca spirele sunt destul de dese, campul magnetic in interiorul solenoidului este uniform si oriental axial. (= const.).

- in al doilea rand, daca solenoidul este destul de lung, campul magnetic in exteriorul solenoidului este de multe ori mai slab ca cel din interiorul si poate fi neglijat intr-o prima aproximatie (

Sa calculam campul magnetic intr-un punct P din interiorul solenoidului. In acest scop vom alege un drum de integrare convenabil, care sa treaca prin P. Fie acest drum conturul dreptunghiular ACDFA. Legea lui Ampére aplicata la acest contur are forma

(15.10)

Calculul circulatiei vectorului de-a lungul conturului inchis va consta in calcularea integralelor de linie in lungul celor patru laturi. Pe drumul DF, in exteriorul solenoidului, putem aproxima campul magnetic ca fiind zero. In lungul laturilor CD si AF ale dreptunghiului, fie ca este zero (in exteriorul solenoidului) fie ca este perpendicular pe (in interiorul solenoidului). Rezulta ca integralele de linie din produsul pe laturile DE, CD si AF sunt nule. In interiorul solenoidului, este constant si paralel cu pe toata lungimea AC, astfel ca putem scrie:

(15.11)

unde d este lungimea laturii AC a dreptunghiului considerat. Curentul I_ACDFA din relatia (15.10) este egal cu suma celor n.d curenti de intensitate I, avand toti acelasi sens:

I_ACDFA = n.d.I (15.12)

Din ultimele trei relatii obtinem ca:

B = (15.13)

Formula (15.13) a fost dedusa pentru cazul ideal al unui solenoid foarte lung (teoretic infinit) si bobinat spira langa spira. In cazul unui solenoid de lungime l, avand N spire, putem scrie n =N/l si relatia de mai sus devine:

B = (15.14)

Formula (15.14) permite calcularea valoarea campului magnetic in punctele din interiorul solenoidului suficient de departate de extremitatile acestuia.

Calcule mai riguroase arata ca, in cazul unui solenoid foarte lung, campul magnetic pe axa solenoidului la extremitati este jumatate din valoarea campului in centrul sau.

15.4. Fluxul campului magnetic

Ecuatia (15.8) care exprima legea lui Ampére nu este suficient pentru a determina campul magnetic cand densitatea de curent este data, deoarece mai multe campuri vectoriale pot avea acelasi rotor. Reamintim ca in cazul campului electrostatic am obtinut doua relatii fundamentale calculand rotorul si divergenta vectorului . Pentru a calcula divergenta vectorului va trebui sa ne ocupam de fluxul liniilor campului magnetic. Fluxul magnetic prin suprafata elementara dS (fig.15.3) este = iar fluxul total prin suprafata S, va fi:

(15.15)

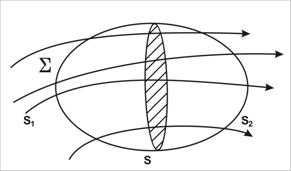
Fig.15.4 Fluxul magnetic prin suprafata Σ  Fig.15.3 Flux magnetic elementar

Sa evaluam acum vectorului printr-o suprafata inchisa.

In acest scop ne folosim de o constatare experimentala fundamentala pentru studiul campului magnetic si anume imposibilitatea obtinerii unor magneti cu un singur pol (monopoli magnetici). In cazul campului magnetic nu exista deci un analog al sarcini electrice. Daca se considera o suprafata oarecare inchisa, , strabatuta de fluxul vectorului (fig.15.4) se poate alege o sectiune S care imparte suprafata in doua suprafete S₁ si S₂ , astfel incat toate liniile de camp care intra prin suprafata S₁ sa iasa prin suprafata S₂ . Este evident ca fluxul prin S₂ va fi egal si de semn contrar fluxului prin S₁ , astfel ca fluxul total prin suprafata inchisa va fi nul.

(15.16)

Aplicand teorema lui Gauss obtinem:

div (15.17)

Relatiile (15.16) si (15.17)) reprezinta forma integrala respectiv diferentiala a legii lui Gauss pentru campul magnetic. Ele permit determinarea valorilor campului magnetic al oricarei distributii de curenti.

INTREBARI

1. Care este originea campului magnetic?

a) campul electric,

b) curentul electric,

c) miscarea sarcinii electrice,

d) existenta electronului,

e) existenta protonului.

2.Cum se exprima legea lui Ampere? Care sunt semnificatiile notatiilor care intervin?

a) , j - densitatea de curent, H- intensitatea campului magnetic,

b) , B- inductia campului magnetic, - permeabilitatea magnetica, H- intensitatea campului magnetic,

c) , H- intensitatea campului magnetic,. - conturul de integrare, I- intensitatea curentului electric,

d) , j - intensitatea curentului electric , H- intensitatea campului magnetic,

e) , B- inductia campului magnetic, - permitivitatea magnetica, H- intensitatea campului magnetic,

Liniile campului magnetic sunt continue, spre deosebire de liniile campului electrostatic, care sunt discontinue. Prin ce relatie se poate exprima acest lucru?

a)

b)

c) div =0

d) grad= 0

e)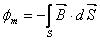