Consecinte cinematice ale transformarilor Lorentz

Un sistem de referinta fata de care un corp este în repaus se numeste sistem de referinta propriu. Marimile raportate la sistemul de referinta propriu se numesc marimi proprii. Astfel, lungimea unui obiect masurata de un observator în repaus fata de acel obiect se numeste lungime proprie, iar durata unui eveniment care se produce într-un punct fix (sau intervalul de timp între doua evenimente care se produc în acelasi punct aflat în repaus fata de sistemul propriu) se numeste durata proprie.

a) Contractia lungimilor în directia de deplasare

Sa consideram o bara paralela cu axa Ox a unui referential (R), în repaus fata de acest referential si un observator care este si el în repaus fata de (R). Acest observator vizeaza capetele barei si gaseste abscisele lor ,respectiv , calculând lungimea proprie .

Sa consideram un alt observator care se misca rectiliniu si uniform fata de (R), pe directia barei si operatia de masurare a absciselor extremitatilor barei. Acest al doilea observator (care face parte dintr-un referential (R')) trebuie sa masoare ambele abscise la acelasi moment t' si gaseste valorile , respectiv , calculând lungimea cinematica a barei .

Putem gasi relatia între lungimea proprie si cea cinematica folosind transformarile Lorentz (I.30):

adica:

Se observa ca , adica lungimea proprie este cea maxima. Toti observatorii din sisteme în miscare fata de bara o "vad" mai scurta.

S-a obtinut asadar contractia lungimilor în directia de deplasare. Scurtarea barei nu este reala , ea nu sufera nici o modificare, nu apar tensiuni sau deformari care sa antreneze contractia.

Lungimea este o lungime reala, fiind unica; lungimea l este o lungime aparenta, putând exista o infinitate de valori pentru ea, în func# 141g69b 5;ie de viteza observatorului. Consideram doua rigle identice (1) si (2), care au lungimi identice când sunt masurate de un observator O în repaus fata de ele (în referentialul (R)). Presupunem ca rigla (2) se misca cu viteza v fata de rigla (1). Un observator din (R) vede rigla (1) fixa, ea având în continuare lungimea , însa rigla (2) va fi mobila, acest observator masurând . Pentru acest observator rigla (2) e mai scurta ().Consideram acum un observator legat de rigla (2) în miscare (din (R'));el va masura pentru rigla (2) (fixa fata de el) lungimea , iar pentru rigla (1) (care este mobila fata de el) lungimea .Pentru acest observator rigla (1) este mai scurta (). Relatiile obtinute par contradictorii, dar de fapt ele nu se pot compara pentru ca prima () a fost obtinuta cu rigle si ceasuri din referentialul (R), iar a doua () -cu rigle si ceasuri din (R'). Contractia relativista a lungimilor este deci o consecinta a operatiei de masurare. Pentru dimensiunile transversale ale corpurilor nu se obtin rezultate diferite când sunt masurate de diferiti observatori, astfel ca un volum elementar propriu masurat de un observator în miscare devine:

Ca urmare, forma cinematica a corpurilor e "turtita" în directia miscarii fata de forma proprie: o sfera este sesizata ca atare de catre un observator în repaus fata de ea, dar vazuta "elipsoid de rotatie" de un observator în miscare.

b) Dilatarea relativista a duratelor

Fie doua evenimente (de exemplu începutul si sfârsitul unui fenomen) care se petrec în acelasi punct de abscisa x, imobil în (R), la momentele respectiv .

Durata proprie va fi:

si este masurata cu un ceas din (R).

Consideram un observator dintr-un referential (R') care se misca cu viteza constanta v fata de (R), de-a lungul axei Ox. Cu un ceas din (R') observatorul masoara momentele si ale celor doua evenimente si obtine durata cinematica a fenomenului . Folosind transformarile Lorentz (I.29) obtinem:

Se observa ca deci duratele apar dilatate; durata proprie este minima. Orice fenomen se petrece mai lent pentru un observator în miscare fata de locul unde se desfasoara fenomenul, decât pentru observatorul aflat la o distanta fixa de acel loc.

Dilatarea duratelor, exprimata de relatia (I.33) a initiat în teoria relativitatii restrânse problema denumita a "calatorului lui Langevin" si aceea a "paradoxului gemenilor". În 1911, Langevin a aplicat relatia (I.33) fenomenelor biologice tragând concluzia ca miscarea sistemelor inertiale trebuie sa încetineasca si aceste fenomene.

Astfel, daca este viata unui om (intervalul dintre momentul nasterii si cel al decesului), urmeaza, sustine Langevin, ca într-un sistem inertial în miscare viata este mai lunga, are un ritm de evolutie mai lent decât în altul, adica dilatarea duratelor are ca efect prelungirea vietii. "De aceea - scrie Langevin - oricare dintre noi poate sa piarda numai doi ani din viata lui pentru a sti ce va fi cu Pamântul peste 200 de ani.Nu are decât sa se închida într-un proiectil care ar porni de la Pamânt cu o viteza ceva mai mica decât cea a luminii, potrivind lucrurile astfel încât, dupa un an-socotit de el-sa întâlneasca un corp ceresc, de unde sa porneasca înapoi cu aceeasi viteza. Ajuns pe Pamânt, dupa o lipsa de doi ani, el va gasi globul îmbatrânit cu 200 de ani daca viteza sa a fost mai mica cu 1/20000 din viteza luminii."

Sa calculam exact viteza calatorului lui Langevin pentru ca doi ani () din viata sa sa corespunda la 200 de ani ()din viata oamenilor de pe Pamânt.

,de unde v = 299985 km/s, cu 15km/s mai mica decât c.

Einstein a fost complet de acord cu Langevin, deoarece, tot în 1911 scria: "Daca am introduce un organism viu într-o cutie si l-am face sa întreprinda o calatorie dus-întors, s-ar putea ca acest organism, dupa un zbor cât de îndelungat, sa se întoarca la locul de plecare foarte putin schimbat (cât de putin vrem), în vreme ce organisme exact la fel alcatuite, care au ramas la locul lor, au facut de mult loc altor generatii." Cu astfel de concluzii senzationale nu este de mirare ca teoria relativitatii a stârnit un interes deosebit.

În concluziile mentionate se uita însa ca relatiile din teoria relativitatii restrânse sunt valabile numai pentru sisteme inertiale (vehiculul cosmic al lui Langevin nu este un asemenea sistem).

"Paradoxul gemenilor" constituie o varianta a experientei imaginate de Langevin. Sa presupunem ca, în momentul când sistemele inertiale (R) si (R') încep sa se miste, unul în raport cu celalalt, cu o viteza apropiata de cea a luminii, se nasc doi gemeni. Unul este "retinut" în (R), iar celalalt este "trecut" în (R'). Observatorul din (R) urmareste evolutia geamanului din (R'); el constata ca acesta se dezvolta mult mai încet decât fratele lui din (R). Când copilul din (R') a împlinit un an, fratele sau din (R) îsi sarbatoreste centenarul. "Este într-adevar o concluzie ciudata-scrie Max Born- care însa nu poate fi eliminata prin nici un fel de interpretare."

S-a pierdut totusi din vedere faptul ca intervalele de timp în fiecare sistem se masoara cu ceasuri diferite ("cu ani diferiti"). Ceasurile din fiecare referential masoara timpii proprii în acel referential. În acest fel, o zi pe racheta este facuta sa dureze cât aproximativ 3 luni pe Pamânt sau un an pe racheta dureaza cât 100 de ani terestrii. Astfel, timpul brut este acelasi, dar rezultatul masurarii lui cu unitati de masura diferite va fi diferit.

Având în vedere legea invariantei timpului brut ("pentru toti observatorii unui fenomen fizic, produsul dintre intervalul de timp masurat si unitatea de timp respectiva are aceeasi valoare") cele doua probleme în discutie (a calatorului si a gemenilor) înceteaza sa mai fie paradoxuri.

Vom prezenta în continuare problema dezintegrarii miuonilor care si-a gasit o explicatie stralucita în cadrul teoriei relativitatii restrânse.

Miuonii sunt particule din radiatia cosmica cu masa de repaus (-masa de repaus a electronului), ce iau nastere la o altitudine de câtiva kilometri si se dezintegreaza spontan într-un electron, un neutrino si un antineutrino.

În 1963, D.H.Frisch si J.H.Smith au aratat ca un contor instalat la o altitudine de 1910m înregistreaza în fiecare ora câte 563 de miuoni cu viteza v = 0,994c, însa la nivelul marii contorul înregistreaza numai 408 miuoni pe ora deoarece, în timpul parcursului, o parte din ei se dezintegreaza. Sa denumim "timp de dezintegrare" intervalul în care numarul de miuoni scade de la 563 la 408 pe ora. Acest timp poate fi calculat de doi observatori:

a) un observator O' în repaus fata de fenomenul de dezintegrare, foloseste legea dezintegrarii radioactive:

unde este viata medie a particulelor (determinata în laborator), , , . Se obtine .

b) un observator O fata de care miuonii sunt în miscare rationeaza astfel: în timp ce miuonii se dezintegreaza în limitele indicate de contori, ei strabat uniform distanta L = 1910m, cu v = 0,994c.

Timpul de viata va fi :, deci un exemplu tipic de dilatare a duratelor.

Tot acest al doilea observator ar putea aplica legea dezintegrarii radioactive (are acelasi aspect!):

,

numai ca ar fi viata medie în sistemul în miscare. Folosind (experimental), se obtine . Folosind teoria relativitatii restrânse,

, rezultat în buna concordanta cu cel obtinut din experiment.

Drumul l pe care îl pot strabate miuonii în decursul vietii medii este, pentru observatorul O:

,

adica o lungime superioara distantei de 1910m, ceea ce justifica prezenta miuonilor la nivelul marii. Daca am considera viata medie (cea proprie) pentru toti observatorii, drumul lor ar fi: , deci miuonii nu ar mai putea ajunge la nivelul marii. Pentru teoria relativitatii restrânse, l si l' reprezinta lungimea proprie respectiv lungimea cinematica a parcursului lor. Se verifica relatia:

.

Înregistrarea miuonilor la nivelul marii confirma faptul ca durata lor medie de viata este dilatata pentru observatorul fata de care sunt în miscare, în raport cu durata - durata proprie de viata.

În acest fel rezultatul experientei Frisch-Smith este explicat, teoria relativitatii restrânse confirmându-se în mod stralucit.

c) Relativitatea simultaneitatii

Vom arata ca nu se poate vorbi despre o simultaneitate absoluta a fenomenelor, adica, daca doua evenimente sunt simultane într-un referential, ele pot sa nu mai fie simultane în alt referential.

Sa presupunem ca în punctele si dintr-un referential (R) au loc doua evenimente simultane, la momentul t si sa vedem cum apar aceste evenimente pentru un observator dintr-un referential (R') în miscare rectilinie si uniforma cu viteza v paralela cu Ox fata de (R). Conform relatiei (I.29.d):

si cum , adica evenimentele nu mai apar simultane pentru observatorul mobil.

Conditia de simultaneitate în (R') este satisfacuta numai daca evenimentele se produc si în acelasi punct din (R). În acest caz se spune ca evenimentele se gasesc în coincidenta absoluta.

În concluzie: daca doua evenimente sunt simultane într-un referential (R), ele nu mai sunt simultane în nici un referential care se afla în miscare uniforma fata de (R) decât daca ambele se petrec în acelasi punct din spatiu.

d) Compunerea relativista a vitezelor

Una din concluziile experientelor premergatoare teoriei relativitatii restrânse a fost invaliditatea regulii Galilei de compunere a vitezelor comparabile cu cea a luminii.

Pe baza relatiilor Lorentz (I.29) sau (I.30) se pot stabili noi formule de compunere a vitezelor.

Consideram un punct material care se deplaseaza cu viteza în raport cu un referential (R) si cu fata de referentialul (R') în deplasare uniforma cu viteza paralela cu Ox fata de (R).

Componentele vitezei se calculeaza dupa relatiile:

iar ale vitezei dupa relatiile:

Diferentiind relatiile (I.29) obtinem:

astfel ca :

Transformarile inverse vor fi:

Daca si , Regulile (I.38) sau (I.39) verifica principiul de corespondenta; astfel, daca v<<c , , adica s-au obtinut regulile Galilei de compunere a vitezelor.

Sa aratam ca relatiile (I.38) sunt compatibile cu principiul al doilea al teoriei relativitatii restrânse.

a) Presupunem ca fata de (R), u=c (punctul material este un foton care se deplaseaza paralel cu Ox); atunci, folosind (I.38.a) obtinem:

,

adica si fata de referentialul (R') viteza luminii este aceeasi.

b) Presupunem ca referentialul (R) se deplaseaza cu v=-c fata de referentialul (R') si dintr-o sursa din (R) se emite un semnal luminos, paralel cu Ox, adica u = c. Un observator din (R') va gasi:

,

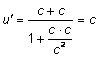adica viteza luminii nu depinde de viteza sursei.

c) Daca semnalul luminos este paralel cu axa Oy, atunci , deci

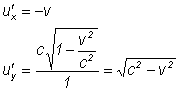
iar

deci viteza luminii nu depinde de directia de propagare sau de cea de masurare.

e) Efectul Doppler-Fizeau relativist

Efectul Doppler-Fizeau consta în modificarea frecventei unei unde receptionate fata de frecventa undei emise daca receptorul (observatorul) si sursa (emitatorul) se afla în miscare relativa.

Efectul este cunoscut din mecanica newtoniana, gasindu-se relatiile:

când sursa este mobila si observatorul fix si:

când sursa este imobila, iar observatorul mobil, unde este frecventa receptata, -frecventa emisa, v-viteza relativa a sursei fata de observator.

În mecanica prerelativista efectul Doppler transversal (produs când directia de deplasare relativa si directia de propagare a undei sunt perpendiculare) nu s-a putut explica, desi a fost constatat experimental. În plus, s-a constatat experimental ca, pentru lumina, modificarea frecventei este aceeasi indiferent daca observatorul este fix si sursa se deplaseaza sau invers.

În mecanica relativista, relatia dintre cele doua frecvente reiese din invarianta ecuatiei undei fata de transformarile Lorentz.

Presupunem un referential (R) în originea caruia se afla un observator (receptor) si un referential (R') care se misca cu viteza v constanta, paralela cu axa Ox fata de (R), în originea caruia se afla o sursa de unde S (figura I.5).

Presupunem ca vectorul de unda al undei emise este în planul x'Oz' si face un unghi cu axa Ox', astfel încât:

(am presupus ca este vorba de o unda luminoasa, cu pulsatia ).

Solutia ecuatiei undelor pentru o unda armonica plana are forma:

.

(aici reprezinta marimea fizica ce oscileaza în timp si spatiu, în cazul undei electromagnetice fiind intensitatea câmpului electric sau intensitatea câmpului magnetic.)

Pentru unda emisa:

iar pentru unda receptata:

unde este pulsatia undei receptate sub unghiul fata de axa Ox din referentialul (R).

Invarianta celor doua solutii (I.42) si (I.43) presupune egalitatea celor doua faze:

Folosind relatiile lui Lorentz (I.30), din relatia (I.44) obtinem:

care dupa regruparea termenilor devine:

.

Prin identificarea coeficientilor lui t' din aceasta relatie se obtine relatia între pulsatii:

sau între frecvente:

Cazuri particulare

a) Efectul Doppler-Fizeau longitudinal are loc când unda este receptionata de catre observatorul O de-a lungul axei Ox (directiei de miscare relativa a sistemelor).

În acest caz , iar (I.45) devine:

(semnul superior este pentru - sursa se apropie - iar cel inferior pentru - sursa se departeaza)

Dependenta de raportul v/c a pulsatiei receptate este reprezentata în figura I.6.

Se observa ca pentru v=0, ; daca sursa se îndeparteaza de observator, v>0 iar ; daca sursa se apropie de observator v<0, iar . Când v = c frecventa receptata poate deveni nula când sursa se îndeparteaza sau infinita când sursa se apropie de observator.

b) Efectul Doppler-Fizeau transversal se produce când unda este receptionata dupa o directie perpendiculara pe cea de deplasare relativa a sistemelor.

În acest caz , iar relatia (I.45) devine:

deci , indiferent daca sursa se apropie sau se îndeparteaza. Functia este reprezentata în figura I.7.

În general, pentru , aspectul functiei este redat în figura I.8.

Se observa ca exista o viteza critica de apropiere pentru care frecventa receptata este maxima. Punând conditia:

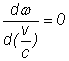
se obtine viteza critica (la apropiere) si

Se observa de asemenea ca relatia (I.46) satisface principiul de corespondenta; la limita se obtine relatia (I.40.b).

Daca se considera sursa fixa (în R) si observatorul mobil (în R ) rezultatele sunt identice, confirmând experimentul.

Efectul Hubble

În 1912 Slipher observa ca liniile spectrale emise de galaxii prezinta o "deplasare spre rosu", adica lungimile lor de unda sunt mai mari decât cele ale acelorasi linii spectrale emise de surse de pe Pamânt. Cresterea lungimii de unda se datoreaza scaderii pulsatiei ().

În 1929 Hubble trage concluzia ca în raport cu un punct de observatie dat, toate galaxiile se îndeparteaza cu o viteza proportionala cu distanta dintre acest punct de observatie si galaxie. Hubble da o lege pentru viteza de îndepartare a galaxiilor:

v=hl

unde si se numeste constanta lui Hubble. Pentru o crestere a distantei cu ani lumina se obtine o viteza v = 15 km/s.