Corelatia partiala

Corelatia partiala

Conceptul de corelatie

Conceptul de corelatie se bazeaza pe conceptia lui Galton si Pearson conform careia cauzalitatea este doar limita extrema categoriei de relatie între doua fenomene. Ca urmare, principiul explicator 828d37i al faptelor si fenomenelor ar putea fi extins de la riguros demonstrata "cauzalitate", specifica stiintelor fizice si naturale, la cel de "asociere", care poate fi pus mai usor în evidenta în lumea realitatii social-umane, în care cauzalitatea are un caracter prea complex pentru a fi întotdeauna pusa în evidenta. Desi mai putin riguroasa, asocierea fenomenelor poate fi pusa în evidenta prin masurarea variatiei lor concomitente, indiferent de natura exacta, adesea insondabila a cauzei care produce aceasta co-variatie. Este suficient sa obtinem masuratori concomitente ale unor variabile pentru a fi în masura sa aflam gradul lor de variatie reciproca. Astfel s-a deschis posibilitatea de a se aduce în domeniul stiintelor sociale si umane rigoarea specifica stiintelor fizice si naturale.

Precursorul teoretic al coeficientului de corelatie este coeficientul de covarianta. El se defineste ca suma a produselor dintre valorile celor doua variabile, raportata la numarul perechilor de valori din cele doua distributii.

Problema pe care o avem cu coeficientul de covarianta este aceea legata de unitatile de masura. Valorile perechi se pot exprima fiecare în unitati de masura diferite, ceea ce poate face dificila interpretarea semnificatiei coeficientului. Solutia problemei consta în transformarea valorilor celor doua variabile în scoruri standard, ceea ce produce un rezultat care nu mai are legatura cu unitatea de masura. Ca urmare, formula de definitie a coeficientului de corelatie Pearson (r), probabil unul dintre cele mai utilizate teste utilizate în statistica aplicata la stiintele social-umane, este:

unde z_x si z_y sunt transformarile în note standard z ale variabilelor x, respectiv y, iar N este volumul esantionului.

Nu facem decât sa reamintim aici ca r poate lua valori pe o plaja între +1 (corelatie pozitiva, directa, perfecta) si -1 (corelatie negativa, inversa, perfecta). Între aceste limite extreme, un coeficient de corelatie 0 (zero), indica absenta totala a corelatiei sau, cu alte cuvinte, independenta acestora una fata de alta. Pe de alta parte, coeficientul de corelatie Pearson se bazeaza pe un model de asociere liniara între variabile. De aceea, absenta unei valori suficient de mari, ori semnificative, nu exprima neaparat absenta unei legaturi între variabile ci, poate, existenta unui alt tip de variatie concomitenta decât cel liniar (curbiliniu). Mai adaugam, de asemenea, ca în studiile bazate pe coeficientul de corelatie nu avem variabila "independenta", ambele variabile fiind considerate "dependente". Cu alte cuvinte, nici una variabile nu este considerata ca având o "influenta" asupra celeilalte (cel putin din punctul de vedere al rationamentului statistic).

Conceptul de corelatie partiala

Asa cum am vazut, coeficientul de corelatie masoara gradul de variatie simultana dintre doua variabile, considerate fara nici o legatura cu alte variabile. Dar putine aspecte ale realitatii social-umane interactioneaza în mod izolat de altele. Regula este, mai degraba, aceea de a avea interconditionari multiple. Variatia concomitenta a doua variabile poate fi determinata de o legatura intrinseca dintre ele si, în acelasi timp, de o anumita influenta pe care fiecare o suporta din partea uneia sau mai multor variabile de alta natura. Cu alte cuvinte, putem avea efecte exterioare care sa contribuie la marimea coeficientului de corelatie bivariata. De exemplu, putem obtine o corelatie negativa, puternica si semnificativa, între lungimea parului si înaltime (persoanele scunde au parul mai lung). Daca, însa, luam în considerare influenta variabilei "sex", si îi excludem efectul (deoarece femeile sunt, de regula, mai scunde decât barbatii), atunci este foarte posibil sa obtinem o cu totul alta valoare a corelatiei dintre lungimea parului si înaltime, cel mai probabil mai mica si nesemnificativa. Sa luam si un alt exemplu: Se initiaza un studiu cu privire la relatia dintre nivelul salarizarii si vârsta. Rezultatele ne pot indica o legatura semnificativa între aceste doua variabile dar, daca izolam efectul nivelului de instruire, putem ajunge la un coeficient de corelatie mai mic decât cel obtinut initial (ceea ce sugereaza ca, nu atât vârsta în sine, cât timpul alocat procesului de instruire este factorul determinant al nivelului de salarizare atins).

Solutia statistica a problemei enuntate mai sus este coeficientul de corelatie partiala care ne ofera o posibilitate de calculare a corelatiei dintre doua variabile cu mentinerea constanta a influentei externe din partea uneia sau mai multor variabile. Chiar daca în exemplele prezentate am sugerat doar influenta unei a treia variabile, modelul de analiza, dar si cel de calcul, al corelatiei partiale pot fi extinse la oricât de multe variabile externe.

Coeficientul de corelatie partiala nu este inclus în mod obisnuit printre testele statistice multivariate, Consideram, însa, ca introducerea lui aici este justificata, pe de o parte, ca o dezvoltare necesara a atât de utilizatului coeficient de corelatie si, pe de alta parte, de faptul ca, totusi, în acest caz se iau în analiza mai mult de doua variabile. Chiar daca celelalte doar pentru a le fi anihilate efectul (contributia).

Calcularea coeficientului de corelatie partiala

Formula de calcul pentru coeficientul de corelatie partiala este urmatoarea:

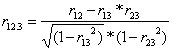
Unde:  r_12.3 este corelatia partiala dintre variabila 1 si variabila 2 cu izolarea efectului variabilei 3; r₁₂ este corelatia dintre variabila 1 si 2; r₁₃ corelatia dintre variabila 1 si 3 iar r₂₃ corelatia dintre variabila 2 si 3.

În cele ce urmeaza, vom prezenta modul de calcul al coeficientului de corelatie partiala prin utilizarea programului SPSS.

Sa luam în considerare un studiu ipotetic al carui scop ar fi evidentierea relatiei dintre rezultatele la un test de reprezentare spatiala si cele ale unui test de calcul aritmetic. Totusi, ne putem pune problema influentei inteligentei asupra celor doua tipuri de performanta, motiv pentru care aplicam si un test de inteligenta. Matricea de date, introdusa în Editorul de date SPSS, arata ca mai jos:

Pentru a fi sigur cu privire la relatia dintre variabilele care îl intereseaza, fara a suporta efectul celei de a treia, vom proceda la calcularea coeficientului de corelatie partiala, care se lanseaza în executie din meniul Statistics-Correlate-Partial, cu deschiderea casetei Partial Correlation, în care variabilele cercetate sunt trecute in lista Variables, iar variabila pe care dorim sa o izolam, în lista Controlling for:

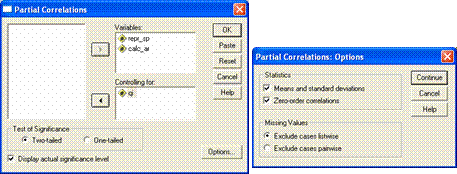
Actionam butonul Options, care deschide caseta corespunzatoare, unde bifam optiunile Means and standard deviation (daca dorim sa avem statistica descriptiva a variabilelor) si, mai ales, Zero-order correlations, pentru a obtine si matricea de corelatie a tuturor variabilelor, fara eliminarea vreuneia dintre ele.

Primul lucru pe care îl analizam în fereastra Output este matricea corelatiilor complete, care apare ca în imaginea alaturata si nu este diferita de matricea produsa de procedura corelatiei bivariate. În acest caz avem o matrice de corelatie cu trei perechi de câte doua variabile, a caror variatie presupunem ca se intersecteaza. Din acest motiv, semnificatia coeficientilor nu poate fi acceptata ca si cum variabilele ar fi total independente (presupunerea tipica pentru corelatia bivariata). Asa cum stim, fiecare dintre coeficientii de corelatie este purtator al unei Erori de tip I (probabilitatea de a respinge ipoteza de nul, desi ea ar putea fi adevarata). Acceptând acest lucru ar însemna ca, la un set de trei coeficienti de corelatie, cantitatea de eroare de tip I ar însuma 0.15 adica de trei ori 0.05, cea ce este inacceptabil. Ca urmare, se aplica metoda Bonferonni de control pentru "eroarea de tip I", la ansamblul celor trei perechi de corelatii: 0.05/3=0.017. Adica, se repartizeaza în mod egal valoare lui alfa pentru un singur test (0.05) la toti cei trei coeficienti calculati. Nu ne ramâne decât sa constatam daca coeficientii obtinuti sunt semnificativi la acest prag de siguranta. Dupa cum se observa, privind fie deasupra, fie sub diagonala matricei, în toate cazurile coeficientii de corelatie dintre cele trei variabile sunt semnificativi la un p<0.017 ceea ce sugereaza ca toate perechile de variabile coreleaza semnificativ. Principala concluzie este aceea ca ambele variabile cercetate (reprezentarea spatiala si operatiile aritmetice) au o variatie comuna, semnificativa, cu inteligenta.

Mai departe, citim rezultatul procedurii de calcul dupa ce influenta inteligentei a fost eliminata:

Din matricea alaturata se observa ca, dupa excluderea contributiei variabilei QI, corelatia celorlalte doua variabile devine 0.094, care corespunde cu p=0.823. Astfel ajungem la concluzia de acceptare a ipotezei de nul (inexistenta unei asocieri între reprezentarea spatiala si capacitatea de calcul aritmetic[1]). Cu alte cuvinte, ceea ce parea a fi o legatura între reprezentarea spatiala si operarea aritmetica nu era decât efectul "influentei" pe care o exercita inteligenta asupra ambelor variabile.

Daca încercam sa reprezentam relatia dintre cele trei variabile pe o diagrama Venn, ele ar putea arata ca în imaginea alaturata. Variabilele Repr_sp si Calc_ar au în comun cu variabila QI o mare cantitate de variatie care se traduce într-un "fals coeficient de corelatie" între ele. Odata înlaturata influenta QI, relatia dintre reprezentarea spatiala si operarea aritmetica apare în adevarata ei lumina, adica fara nici o relevanta.

Interpretarea coeficientului de corelatie partiala

Valorile si modul de interpretare a coeficientului de corelatie partiala sunt întru-totul similare coeficientului de corelatie bivariat. Diferenta consta doar în mentionarea eliminarii efectului sau efectelor externe din partea altor variabile. Utilizarea sa aduce mai multa informatie, tocmai pentru ca permite cercetatorului sa ia în calcul relatii mai complexe dintre variabile decât cele specifice statisticii univariate tipice.

Asa cum am spus deja, avem o corelatie perfecta atunci când r este egal cu +1 sau -1. Interpretarea coeficientului de corelatie tine cont de doua aspecte: semnificatia si marimea. Un coeficient de corelatie care se afla sub pragul de semnificatie (nivelul alfa), fixat anterior analizei calculelor, nu va putea fi luat în discutie, indiferent de valoarea lui r. Desigur, atunci când aceasta valoare este promitator de mare iar studiul nu s-a bazat decât pe un numar relativ mic de subiecti, se poate avea în vedere reluarea cercetarii pe un esantion cu mai muti subiecti. În ceea ce priveste valoarea în sine a lui r, desigur, cu cât este mai mare, cu atât ea exprima o asociere mai intensa între variatiile concomitente dintre cele doua variabile. De-a lungul timpului au fost propuse diverse astfel de scale de valorizare. Astfel, Jacob Cohen, într-o lucrare clasica sugera ca o corelatie de 0.5 este "mare" pe când una de 0.1 este "mica". De aici ar rezulta ca toate valorile peste 0.5 sunt "mari", cele între 0.3 si 0.5 sunt "moderate", iar cele între 0.1 si 0.3 sunt "mici". De retinut este în primul rând faptul ca o corelatie sub valoarea de 0.1 va fi considerata ca "neglijabila".

Reluând subiectul într-o maniera analitica, Hopkins[3] propune o varianta mai sensibila de interpretare a valorii coeficientilor de corelatie, dupa cum urmeaza:

În orice caz, prima conditie pentru a lua în considerare existenta unei corelatii între doua variabile ramâne atingerea pragului de semnificatie (alfa). Daca valoarea lui r corespunde unui nivel alfa mai mare de 0.05, existenta unei corelatii este de neluat în seama, indiferent de marimea coeficientului Pearson. Aceasta, deoarece nu avem temei pentru a accepta ca se îndeparteaza suficient de o valoare care ar fi putut decurge din jocul hazardului.

Mai departe, în interpretarea coeficientului trebuie sa operam cu distinctia dintre "semnificatia statistica" si "relevanta practica" a valorii obtinute. Un coeficient de corelatie puternic semnificativ nu înseamna ca are, automat, si o relevanta practica pe masura. Ne ajuta în întelegerea acestei distinctii ceea ce se numeste "coeficientul de determinare" si care nu este altceva decât valoarea lui r ridicata la patrat. Coeficientul de determinare este utilizat în mod uzual în forma sa procentuala (r²_*100) si indica procentul de varianta pe care cele doua variabile o au în comun. Cu alte cuvinte, cît la suta din gradul de împrastiere a fiecarei unei variabile este "determinat" de variatia (împrastierea) celeilalte variabile. Daca observam cu atentie tabelul alaturat, vom observa ca valoarea coeficientului de determinare scade mult mai accentuat decât valorile lui r , datorita efectului ridicarii la patrat a unor numere subunitare.

Daca obtinem un r=+0.80 între inteligenta si performanta scolara, vom putea spune ca doar 64% din variatia celor doua variabile este comuna, restul de 36% datorându-se altor influente. Ca regula generala, la capatul procedurii de testare a corelatiei se recomanda interpretarea coeficientului de determinare si nu a celui de corelatie, acesta din urma sugerând o covarianta mai mare decât exista în mod real.

În cele din urma, ce trebuie sa luam în considerare, semnificatia sau intensitatea asocierii? Desigur, raspunsul este unul relativ. Daca finalitatea studiului este aceea de a lua decizii, ca în cazul selectiei de personal, de exemplu, se vor cauta valori cât mai mari ale coeficientului de corelatie (r), implicit ale celui de determinare (r²). Dar daca obiectivul este preponderent teoretic, de a pune în evidenta relatii "ascunse" între variabile, atunci indiferent de marimea lor, coeficientii de corelatie vor fi luati în considerare (desigur, daca sunt mai mari de 0.1).

Limitele de încredere pentru coeficientul de corelatie

Semnificatia limitelor de încredere

Atunci când calculam coeficientul de corelatie pentru valorile masurate pe un esantion o facem, desigur, cu scopul de a avea o estimare asupra gradului în care cele doua variabile au o variatie comuna la nivelul întregii populatii. Deoarece calcularea corelatiei pe "valorile populatiei" este practic imposibila, tot ce putem face este sa o estimam, cu o anumita marja de eroare, prin utilizarea esantionului. Astfel, în termeni formali, r (calculat pentru esantion) este o estimare pentru ρ (ro), corelatia "adevarata" la nivelul populatiei. Nu vom putea sti niciodata daca aceasta estimare este corecta, cu exceptia cazului în care am avea acces la toate valorile populatiei, dar putem evalua probabilitatea ca intensitatea asocierii în populatie sa se afle între anumite limite, numite din acest motiv, limite de încredere. Este evident ca, cu cât aceste limite vor fi mai largi, cu atât acuratetea estimarii pentru o anumita valoare calculata a coeficientului de corelatie este mai scazuta. Este evident din cele spuse, ca "distanta" dintre limitele de încredere (superioara si inferioara) este data de "eroarea standard" a valorii calculate a lui r. Adica, de variabilitatea estimata pentru o distributie de coeficienti r, pe care o vom numi r_s (de la sample distribution, distributia de esantionare) daca am efectua corelatii pe toate esantioanele posibile, de aceeasi marime, din respectiva populatie.  

Calcularea limitelor de încredere

Construirea intervalelor de încredere pentru coeficientul de corelatie la nivelul populatiei (ρ) nu este la fel de simpla ca în cazul mediei, de exemplu. Atunci când ρ=0, valorile r_s (cele care ar fi calculate pe esantioanele extrase din aceeasi populatie) ar forma o distributie simetrica, în jurul lui zero ("normala", daca volumul esantionului este suficient de mare). Dar daca ρ=+0.7 distributia lui r_s are o împrastiere asimetrica în jurul lui acestei valori. Motivul este simplu: este mai mult "loc" pentru valori sub +0.7 decât peste aceasta valoare (deoarece stim ca r ia valori între -1 si +1). Cu cît estimarea pentru ρ este mai aproape de limitele teoretice ale lui r, cu atât distributia r_s este mai asimetrica spre parte opusa. Aceasta particularitate creeaza o piedica în transformarea coeficientilor r_s în scoruri Z (cu majuscula, pentru a se evita confuzia cu scorurile z, clasice), necesare construirii limitelor intervalului de încredere pentru ρ. Problema a fost rezolvata de Fisher, care a elaborat un algoritm pe baza caruia valorile r_s sunt transformate în valori Z, a caror arie de distributie sub curba normala este cunoscuta:

z = 0.5log[(1 + r)/(1 - r)]

Pentru a se evita utilizarea acestei formule relativ greoaie, poate fi utilizat un tabel (vezi Anexa) care, chiar daca nu contine toate valorile intermediare, este suficient pentru a acoperi nevoile practice.

Sa luam, ca exemplu, valoarea coeficientului de corelatie partiala obtinut de noi mai sus: r=0.094. Ne propunem sa aflam care sunt limitele de încredere ale acestei valori, adica care este intervalul în care se poate afla o astfel de valoare, cu o probabilitate asumata. De regula, asa cum stim, aceasta probabilitate asumata este de 0.05 sau, exprimata altfel, un nivel de încredere de 95%.

Practic, aflare limitelor se face astfel:

Transformam r calculat în valoare Z, citind tabela Fisher: în cazul nostru, pentru r=0.094 avem o valoare Z=0.095 (o aproximare acceptabila între cele doua valori tabelare apropiate de r-ul nostru). Pe o distributie normala, cum stim ca este distributia Z, stim ca aproximativ 95% dintre valori se întind între -1.96 si +1.96. Adica, pe o distanta de aproximativ doua abateri standard în jurul mediei (abaterea standard a valorilor Z fiind 1).

Calculam eroarea standard a transformarii Z, în formula:

unde N este volumul esantionului

Calculam limita superioara/inferioara a intervalului:, adica:

Limita superioara: 0.095+1.96*0.40=+0.87

Limita inferioara: 0.095-1.96*0.40=-0.68

Limitele astfel calculate sunt exprimate în valori transformate Z, ori noi avem nevoie sa stim limitele pentru coeficientul de corelatie. Ca urmare, facem acum transformarea inversa, citind valorile lui r în tabela Fisher, corespunzatoare celor doua limite de mai sus, exprimate în valori Z:

Limita superioara de încredere pentru r=+0.70

Limita inferioara de încredere pentru r=-0.59

Utilizarea limitelor de încredere

Faptul ca pe o populatie având caracteristicile esantionului nostru, coeficientul de corelatie "adevarat" dintre cele doua variabile are 95% sanse sa se afle oriunde undeva între -0.59 si +0.70. Cu alte cuvinte, poate fi inclusiv 0. Este un argument în plus pentru a accepta ipoteza de nul si a nu accepta ipoteza unei legaturi între cele doua variabile.

Mai trebuie sa observam, de asemenea, ca amplitudinea intervalului de încredere este direct dependenta de volumul esantionului. Cu cât N este mai mare, cu atât valoarea erorii standard tinde sa scada, ceea ce aduce limitele intervalului de încredere mai aproape de valoarea calculata a lui r.

Utilizarea limitelor de încredere pentru interpretarea coeficientului de corelatie este însa mai utila decât pare în exemplul de mai sus care, oricum, se referea la o valoare a lui r insignifianta, de neluat în seama. Iata un alt exemplu, ilustrat grafic. Într-un studiu pe 64 de subiecti, coeficientul de corelatie dintre înaltime si greutate a fost 0.68, cu un interval de încredere cuprins între +0.52 si +0.79, asa cum se vede în imaginea de mai jos:

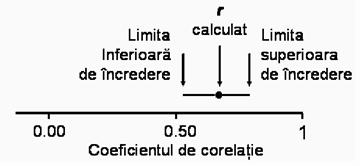
În acest caz limitele de încredere nu intersecteaza valoarea zero, fapt care indica un coeficient de corelatie semnificativ. Dar utilizarea limitelor de încredere ne poate fi de folos si în evaluarea sanselor de a obtine o corelatie semnificativa dupa ce am obtinut un coeficient nesemnificativ. si aceasta datorita evaluarii efectului marimii esantionului.

Sa ne imaginam ca am efectuat un calcul de corelatie pe 30 de subiecti si am obtinut r=0.30. Limitele de încredere pentru acesta sunt între -0.07 si +0.60, ceea ce arata ca este nesemnificativ, dat fiind faptul ca între cele doua limite este si valoarea zero, aceea care este vizata de ipoteza de nul. Dar calculele ne arata ca, daca am creste volumul esantionului la 50 de subiecti limita inferioara trece deja peste valoarea zero. Celelalte linii din tabel prezinta efectul de marime al esantionului în cazul cresterii lui N pâna la 100 de subiecti.

Tabela Fisher de transformare a valorilor r în scoruri Z

(Sursa: https://davidmlane.com/hyperstat/rtoz_table.html)