Cuadrivectori

Cuadrivectorul pozitie-timp este un vector ale carui componente sunt coordonatele de univers x₁=x, x₂=y, x₃=z, x₄=ict ("axele" spatiului Minkowski). El se poate reprezenta printr-o matrice coloana:

Definim matricea transformarii Lorentz:

unde ;

Transformarile Lorentz se vor scrie atunci sintetic prin relatia:

Modulul patrat al cuadrivectorului pozitie-timp va fi

si este un invariant relativist.

2) Cuadrivectorul viteza de univers U are componentele

în care dt₀ este timpul propriu elementar. Pentru o particula care se misca cu viteza v fata de un referential (R), dt₀ este timpul elementar în sistemul atasat particulei; deci în referentialul (R), fata de care particula are coordonatele x_I, elementul infinitezimal de timp va fi dt, legat de dt₀ prin relatia (I.32):

Sa calculam componentele cuadrivitezei de univers:

Atunci cuadriviteza de univers se poate reprezenta prin matricea:

sau

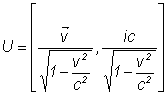
Modulul patrat al cuadrivitezei de univers este

adica este un invariant relativist.

Trecerea de la un referential la altul se face prin relatia

Sa aratam ca relatiile (I.38) de compunere relativista a vitezelor se pot obtine folosind relatia (I.81) de transformare a cuadrivectorului viteza.

Presupunem un punct material care se misca cu viteza u(u_x ,u_y ,u_z) fata de un referential (R); acest punct material va avea viteza (u_x', u_y', u_z') fata de un alt referential (R') care se misca cu viteza v fata de (R) (viteza v este paralela cu Ox).

Cuadrivectorii U si U' se scriu:

Înlocuind în relatia (I.81) si egalând componentele (dupa înmultirea matricelor) avem:

-pentru linia a IV-a:

-pentru linia I:

Folosind relatia (I.83) obtinem:

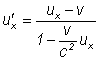
adica tocmai relatia (I.38 a)

-pentru linia a II-a:

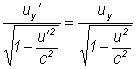
si folosind relatia (I.83), obtinem:

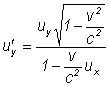
adica tocmai relatia (I.38.b), etc.

3) Cuadriimpulsul - este cuadrivectorului P=m₀U, deci are componentele p_i=m₀u_i (u_i sunt componentele cuadrivitezei).

Pentru un punct material cu masa de repaus m₀ care se misca cu viteza v fata de un referential,

astfel încât primele trei componente sunt componentele carteziene ale impulsului iar cea de-a patra componenta este exprimata prin energia relativista a particulei. Din acest motiv, acest cuadrivector se mai numeste si cuadrivectorul impuls-energie si se scrie concentrat:

Modulul sau:

este un invariant relativist.

4) Cuadrivectorul de unda

O unda este caracterizata de vectorul de unda , al carui modul este, iar directia si sensul sau reprezinta directia si sensul de propagare a undei. În mecanica relativista se defineste cuadrivectorul de unda K, având componentele:

unde, , sunt cosinusii directori ai directiei de propagare fata de axele sistemului cartezian ().

Modulul cuadrivectorului de unda este:

deci este un invariant relativist.

Faza unei unde

se poate scrie ca produsul scalar între cuadrivectorul de unda si cuadrivectorul de pozitie:

Trecerea de la un referential la altul se face prin relatia

Folosind relatia (I.90) putem sa regasim relatia (I.45) de la efectul Doppler-Fizeau.

Într-adevar:

În conditiile mentionate (sursa este în referentialul (R') care se deplaseaza cu viteza v paralela cu axa Ox fata de (R) iar observatorul este fix în (R)), si egalând componentele din linia a patra din ambii membri, obtinem:

sau