DIFRACTIA FRESNEL - OPTICA

UNIVERSITATEA 'POLITEHNICA' DIN BUCUREªTI

CATEDRA DE FIZICÅ

LABORATORUL DE OPTICÅ

DIFRACTIA FRESNEL

DIFRACTIA FRESNEL

Scopul lucrårii

Lucrarea prezintå o metodå de determinare a lungimii de undå pe baza difrac¡iei de tip Fresnel produså pe un orificiu circular.

Teoria lucrårii

Fenomenul de difrac¡ie este un fenomen tipic ce apare la propagarea undei, atunci cand suprafa¡a de undå este limitatå de obstacolele intalnite.

Propagarea undelor in astfel de medii prezintå particularitå¡i determinate de intreruperea par¡ialå sau deformarea frontului de undå de cåtre acestea. Ea are drept consecin¡å abaterea de la propagarea rectilinie a undelor.

Difrac¡ia Fresnel se realizeazå atunci cand sursa se aflå la o distan¡å destul de apropiatå de obstacol, astfel incat curbura fronturilor de undå nu mai poate fi neglijatå.

Consideråm o surså de unde monocromatice S, plasatå in fa¡a unui ecran opac prevåzut cu un orificiu circular. Conform celor discutate anterior se produce fenomenul de difrac¡ie, consecin¡å a faptului cå suprafa¡a de undå sfericå este par¡ial obturatå. (fig. 1)

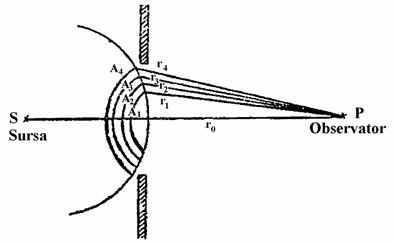
Fig. 1

Datoritå simetriei problemei fa¡å de axa SP, evaluarea intensitå¡ii intr-un punct P situat pe axa SP, poate fi fåcutå simplu prin metoda zonelor Fresnel.

Frontul de undå sferic ce ajunge in fa¡a acestui orificiu se imparte in zone Fresnel, prin aplicarea metodei zonelor lui Fresnel.

Construc¡ia zonelor Fresnel se realizeazå in modul urmåtor: se duce din punctul P o perpendicularå pe suprafa¡a de undå, . Apoi din P se construie¿te, . Existå o familie de drepte cu lungimea , iar locul geometric al intersec¡iei lor cu suprafa¡a de undå este un cerc. Cercul delimiteazå prima zonå Fresnel, de forma unei calote sferice.

Se construie¿te apoi dreapta

A doua zonå Fresnel este o zonå sfericå delimitatå de douå cercuri, intersec¡iile familiilor de drepte ¿i cu suprafa¡a de undå. Analog se construiesc toate zonele Fresnel.

Construc¡ia s-a fåcut respectandu-se condi¡ia geometricå:

(1)

Se observå cå distan¡ele de la cele douå frontiere ale unei zone la punctul P, diferå cu .

Fiecare zonå Fresnel constituie o surså secundarå de unde. Fiecare undå secundarå determinå in punctul de observa¡ie P, cate o oscila¡ie reprezentatå printr-un vector numit fazor, a cårui mårime ¿i fazå este determinatå de drumul optic parcurs de la sursa secundarå (zona Fresnel) panå in punctul de observa¡ie. Prima zonå emite o undå secundarå de amplitudine , a doua zonå emite o undå secundarå de amplitudine ¿.a.m.d.

Din rela¡ia (1) rezultå cå oscilatiile care reprezintå undele in P, de la douå zone vecine sunt in opozi¡ie de fazå.

Undele vecine fiind in opozi¡ie de fazå, amplitudinea rezultantå in P se scrie:

(2)

In cazul discutat, zonele Fresnel avand arii egale, amplitudinile sunt influen¡ate numai de drumurile parcurse de unde ¿i de unghiul de inclinare. Acestea crescand amandouå, amplitudinile undelor secundare descresc odatå cu mårimea rangului zonei Fresnel, adicå:

>>> (3)

Varia¡ia monotonå permite, cel pu¡in intr-o primå aproxima¡ie, så se considere amplitudinea undei provenitå de la o zonå ca media aritmeticå a amplitudinii undelor provenite de la zonele vecine:

(4)

Scriind formula (2) in conformitate cu rela¡ia (4):

..

se observå cå fiecare parantezå din rela¡ia anterioarå este nulå, ceea ce reduce expresia amplitudinii rezultante la:

(5)

cu semnul (+) dacå n este impar ¿i dacå n este par.

Deci amplitudinea rezultantå prezintå o valoare maximå pentru numår impar de zone ¿i o valoare minimå pentru numår par de zone.

Cand n devine foarte mare, devine practic nul ¿i rela¡ia (5) se reduce la , ceea ce aratå cå efectele de difrac¡ie trebuie luate in considera¡ie numai in cazul unui numår mic de zone Fresnel. Dacå numårul acestora este mare, abaterea de la propagarea rectilinie este neglijabilå, obstacolul nefåcand altceva decat så delimiteze fasciculul de unde.

Deoarece intensitatea este propor¡ionalå cu påtratul amplitudinii, intensitatea in centrul figurii de difrac¡ie este maximå pentru un numår impar de zone Fresnel ¿i minimå pentru un numår par de zone Fresnel.

In cazul difrac¡iei Fresnel, figura de difrac¡ie constå din cercuri alternative luminoase ¿i intunecate.

Stabilim acum legåtura intre numårul de zone Fresnel ¿i distan¡a r (pozi¡ia observatorului). Nota¡iile sunt exemplificate in figura (2).

Din rela¡ia (1) rezultå cå:

In triunghiul :

Suprafa¡a de undå avand o curburå micå, neglijand ¿i neglijand ( mic) rezultå:

.

Din triunghiul :

Din ultimele douå rela¡ii rezultå cå:

.

In consecin¡å se ob¡ine ; unde ; .

Suprafa¡a de undå avand o curburå micå, rezultå aria calotei sferice . Ca urmare aria zonei Fresnel cu frontierele ¿i va fi:

Se observå cå ariile zonelor sunt acelea¿i (pentru R ¿i constante) ¿i nu depind de ordinul k al zonei.

Numårul total de zone Fresnel cuprinse in orificiul circular de razå va fi:

Rezultå rela¡ia:

(6)

Rela¡ia (6) aratå cå produsul nr depinde liniar de r. Aceastå rela¡ie stå la baza metodei de determinare a lungimii de undå.

Dispozitivul experimental

Dispozitivul experimental (fig. 3) cuprinde un bec B, dispus la capåtul unui banc optic pe care se aflå: o lentilå ce focalizeazå lumina becului pe o deschidere micå S practicatå intr-o foi¡å metalicå sub¡ire, realizandu-se astfel o surså cat mai punctiformå; un filtru F care selecteazå lumina monocromaticå ce cade pe ecran; ecranul E prevåzut cu orificiul circular de razå pe care se produce difrac¡ia (sistemul permite alegerea a trei valori pentru ); un sistem de vizare alcåtuit dintr-o lentilå .

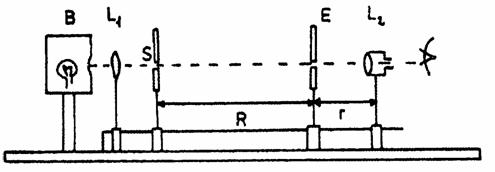
Fig. 3

Modul de lucru

Se alimenteazå becul de la re¡eaua de 220 V c.a. Se regleazå distan¡a intre lentila ¿i deschiderea S astfel incat aceasta din urmå så se afle in focarul lentilei. Se deplaseazå ecranul E panå cand distan¡a R este de aproximativ 50 cm panå la 70 cm. Se are grijå ca E så fie perpendicular pe axa opticå a bancului optic. Se indepårteazå incepand din apropierea ecranului, punandu-se la punct figura de difrac¡ie. Numårul total n al zonelor Fresnel se constatå experimental cå este egal cu suma dintre numårul total al zonelor luminoase (inclusiv zona luminoaså marginalå ce apare totdeauna) ¿i numårul inelelor intunecoase (inclusiv punctul central intunecat ce apare la unele distan¡e). Spre exemplificare, in figura (4), sunt prezentate cateva cazuri.

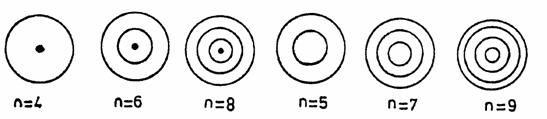
Fig. 4

Indepårtand fa¡å de E, aspectul figurii de difrac¡ie variazå, numårul inelelor scåzand pe måsurå ce ne indepårtåm.

Pentru distan¡a R fixå, se variazå distan¡a r, astfel incat så se ob¡inå una din figurile de difrac¡ie din figura (4).

Pentru o distan¡å R fixå, se determinå r la cel pu¡in cinci figuri de difrac¡ie, corespunzåtoare la numere n de zone Fresnel diferite. Valoarea distan¡ei r se determinå ca medie a cinci måsuråtori. Se repetå måsuråtorile pentru incå douå valori ale distan¡ei R

Rezultatele måsuråtorilor se trec intr-un tabel (vezi pag. 6). Tabelul este intocmit pentru o distan¡å R fixå ¿i un fix. Se vor intocmi trei astfel de tabele (pentru fiecare R fix cate un tabel).

Prelucrarea datelor experimentale

1. Introducand in formula (6) valorile måsurate pentru R, r ¿i n se gåsesc diverse valori pentru lungimea de undå

In continuare se va calcula valoarea medie a lungimii de undå ¿i abaterea standard .

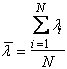; N reprezintå numårul de determinåri pentru .

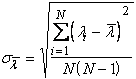
Rezultatul final se va da sub forma:

2. O metodå graficå de mediere este urmåtoarea: se traseazå pe hartie milimetricå pentru fiecare distan¡å R, graficul , care, conform rela¡iei (6), trebuie så reprezinte o dreaptå de pantå .

Se determinå panta dreptei de pe grafic.

Se determinå din rela¡ia:.

Se face media valorilor ob¡inute.

Tabelul este `ntocmit pentru o distan] R fix [i un r fix. Se vor `ntocmi trei astfel de tabele pentru fiecare distan] R fix.

Se då: mm ; = mm ; mm.