Difractia undelor
Daca undele intalnesc obstacole de dimensiuni comparabile ca ordin de marime cu lungimea de unda se produc abateri de la propagarea rectilinie, ceea ce conduce la o redistribuire in spațiu a intensitații undelor, aparand zone de intensitate maxima si respectiv intensitate minima, specifice fenomenului de interferenta.
Astfel, fenomenul de difracție consta in patrunderea undelor in domeniul umbrei geometrice a obstacolelor de dimensiuni mici, comparabile cu lungimea de unda a undelor respective. Ca obstacole putem avea un paravan prevazut cu o fanta mica, sau un obiect netransparent, de o forma oarecare. Explicarea fenomenului de difracție se poate face pe baza principiului Huygens-Fresnel.
7.5.1 Principiul Huygens-Fresnel
O unda reprezinta in general
propagarea unei perturbații din aproape in aproape, in intregul
spațiu. Daca se considera o suprafața inchisa S care inconjoara
izvorul de unde I, este evident ca perturbația va ajunge intr-un punct P
oarecare, aflat in exteriorul suprafeței S, prin intermediul punctelor de
pe aceasta suprafața. Se poate pune intrebarea daca propagarea undelor in
exteriorul suprafeței inchise S nu se reduce la emisia de catre niște
surse dispuse convenabil pe aceasta suprafața (fig.21). 
Raspunsul la
aceasta intrebare il constituie principiul lui Huygen 838g65i s, care afirma ca sursa
primara de unde poate fi inlocuita printr-o distribuție continua de surse secundare punctiforme, convenabil
alese pe suprafața inchisa S, astfel incat rezultanta obținuta prin
suprapunerea undelor secundare in punctul P sa fie identica cu unda primara
emisa de izvorul I, care ajunge in punctul P. Suprafata inchisa S poate fi
particularizata la o sfera sau la un plan, corespunzator formei concrete a
frontului de unda.
Se constata insa ca principiul lui Huygen 838g65i s poate explica patrunderea undelor in regiunea umbrei geometrice, dar nu explica redistribuirea intensitatii undei, adica producerea franjelor de difractie. Ultimul aspect al fenomenului de difractie este explicat printr-o completare adusa de Fresnel la principiul lui Huygen 838g65i s: amplitudinea si faza fiecarei surse secundare sunt egale, in fiecare punct al suprafetei S, cu amplitudinea si faza produse in aceste puncte de catre unda primara. Astfel, potrivit postulatului lui Fresnel, undele secundare de pe suprafata S sunt unde coerente si deci pot introduce fenomenul de interferenta. In acest sens, disfractia poate fi considerata ca o interferenta multipla a undelor secundare, emise de toate sursele plasate pe o suprafata de unda.
Combinatia dintre principiul "de constructie" al lui Huygens cu postulatul interferentei emis de catre Fresnel poarta numele de principiul Huygens-Fresnel.
Fresnel face ipoteza ca amplitudinea ![]() a undei emise de o sursa secundara
a undei emise de o sursa secundara ![]() este proportionala cu aria
este proportionala cu aria ![]() a sursei secundare, si depinde de directia de
propagare. Valoarea amplitudinii
a sursei secundare, si depinde de directia de
propagare. Valoarea amplitudinii ![]() este maxima in sensul de propagare a undei
primare, si nula pe aceeasi directie in sens contrar. Astfel se explica faptul
ca nu apar unde regresive (care s-ar intoarce la sursa principala I), si deci
la fenomenul de interferenta contribuie numai undele secundare progresive (care
se propaga in sens direct).
este maxima in sensul de propagare a undei
primare, si nula pe aceeasi directie in sens contrar. Astfel se explica faptul
ca nu apar unde regresive (care s-ar intoarce la sursa principala I), si deci
la fenomenul de interferenta contribuie numai undele secundare progresive (care
se propaga in sens direct).
Aceasta ipoteza a lui Fresnel este descrisa
matematic prin introducerea unui factor de inclinare![]() , care
descrie variatia cu unghiul
, care
descrie variatia cu unghiul ![]() a amplitudinii
a amplitudinii ![]() a
undelor secundare:
a
undelor secundare:
![]() (7.103)
(7.103)
unde ![]() , pentru
, pentru ![]() si
si ![]() scade la zero pentru
scade la zero pentru ![]() .
.
Din punct de vedere istoric au ramas denumirile de difractie Fresnel - pentru cazul cand difractia se studiaza in lumina divergenta, si difractie de tip Fraunhofer - pentru cazul in cand difractia se studiaza in lumina paralela.
7.5.2 Difractia Fresnel (in lumina divergenta)
Consideram o unda
monocromatica cu lungimea de unda ![]() , ce se
propaga intr-un mediu omogen de la sursa I, ajungand in punctul de observatie
P. In general, sursa I poate fi inconjurata de o suprafata de forma arbitrara.
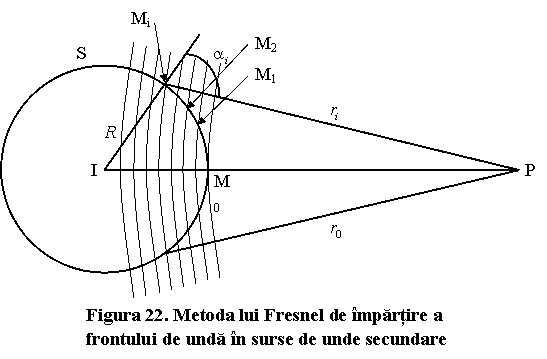
Pentru simplificare alegem o suprafata sferica de raza
, ce se
propaga intr-un mediu omogen de la sursa I, ajungand in punctul de observatie
P. In general, sursa I poate fi inconjurata de o suprafata de forma arbitrara.
Pentru simplificare alegem o suprafata sferica de raza ![]() , centrata pe
sursa I (fig.22).
, centrata pe
sursa I (fig.22).
Potrivit principiului
Huygens-Fresnel, fiecare portiune de pe frontul de unda poate fi considerata o
sursa de unde secundare. Perturbatia ajunsa in punctul de observare P de pe o
portiune de arie ![]() centrata pe punctul
centrata pe punctul ![]() este:
este:
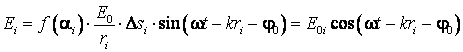 (7.104)
(7.104)
unde:
 (7.105)
(7.105)
este amplitudinea perturbatiei in punctul P datorata undelor secundare ce
se propaga de pe o suprafata de arie ![]() , iar
, iar ![]() este amplitudinea la o distanta egala cu
unitatea de "sursa"
este amplitudinea la o distanta egala cu
unitatea de "sursa" ![]() , si
, si ![]() este faza initiala. Elementul de arie
este faza initiala. Elementul de arie ![]() trebuie ales suficient de mic, astfel incat
marimile
trebuie ales suficient de mic, astfel incat
marimile ![]() si
si ![]() sa ramana constante in limitele acestei arii.
sa ramana constante in limitele acestei arii.

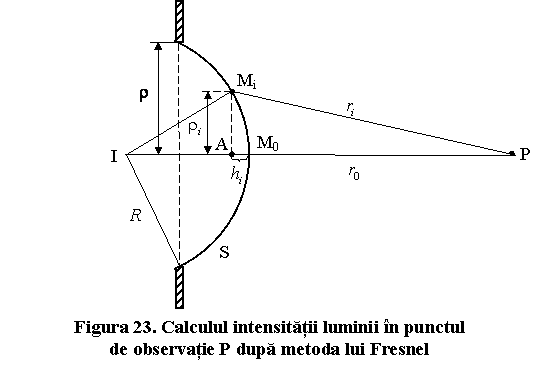
Presupunem ca intre sursa I
si punctul de observare P se sufla un ecran netransparent, in care se practica
o deschidere de raza ![]() (fig.23). Pentru a calcula intensitatea
luminii in punctul P vom utiliza metoda
zonelor Fresnel. Potrivit acestei metode, frontul undei se imparte in zone
inelare cu centrele in punctul
(fig.23). Pentru a calcula intensitatea
luminii in punctul P vom utiliza metoda
zonelor Fresnel. Potrivit acestei metode, frontul undei se imparte in zone
inelare cu centrele in punctul ![]() (fig.22), ducandu-se sfere cu
centrul in P si avand razele
(fig.22), ducandu-se sfere cu
centrul in P si avand razele ![]() .., in asa fel incat:
.., in asa fel incat:
![]() (7.106)
(7.106)
Aceasta inseamna ca sferele cu centrele in P au razele:
![]()
Aceasta impartire a frontului de unda in zone Fresnel prezinta avantajul ca ariile zonelor sunt practic egale, asa cum se demonstreaza in continuare:
![]() (7.107)
(7.107)
Se stie ca aria unui segment
de sfera este ![]() , astfel ca aria zonei Fresnel
cu numarul
, astfel ca aria zonei Fresnel
cu numarul ![]() va fi:
va fi:
![]() (7.108)
(7.108)

Exprimand in triunghiurile IMiA si PMiA cateta comuna MiA :
![]()
obtinem inaltimea ![]() :
:
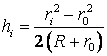 (7.109)
(7.109)
Din relatia ![]() , ridicand la patrat,obtinem:
, ridicand la patrat,obtinem:
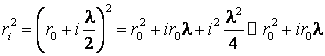
de unde:
 (7.110)
(7.110)
In aproximarea ![]() relatia (7.108)
devine
relatia (7.108)
devine
 (7.111)
(7.111)
Asadar, ariile zonelor
Fresnel nu depind de numarul ![]() , ceea ce
inseamna ca in amplitudinile (7.105) va depinde de
, ceea ce
inseamna ca in amplitudinile (7.105) va depinde de ![]() numai
numai ![]()
Deoarece oscilatiile de la
zonele vecine percurg pana in punctul P distante ce se deosebersc prin
diferenta ![]() , rezulta ca acestea vor
ajunge in punctul P in opozitie de faza :
, rezulta ca acestea vor
ajunge in punctul P in opozitie de faza :
![]() (7.112)
(7.112)
unde ![]() este numarul total de zone Fresnel cuprinse in
deschiderea circulara de raza
este numarul total de zone Fresnel cuprinse in
deschiderea circulara de raza ![]()
Scriind teorema lui Pitagora (fig.23) in
triunghiul ![]() :
:
![]() (7.113)
(7.113)
si neglijand termenul ![]() in aproximatia
in aproximatia ![]() daca tinem seama de (7.110) si de relatia
daca tinem seama de (7.110) si de relatia ![]() , obtinem
, obtinem

Considerand ![]() se obtine numarul total de zone
se obtine numarul total de zone ![]() :
:

Datorita factorului de inclinare ![]() , amplitudinile
, amplitudinile ![]() ale undelor ce ajung in punctul P scad odata
cu cresterea numarului
ale undelor ce ajung in punctul P scad odata
cu cresterea numarului ![]() al zonei,
al zonei, ![]() Considerand aceasta scadere
monotona, amplitudinea corespunzatoare zonei
Considerand aceasta scadere
monotona, amplitudinea corespunzatoare zonei ![]() va fi media aritmetica a amplitudinilor
va fi media aritmetica a amplitudinilor ![]() si
si ![]()
![]()
care se poate scrie si sub forma:
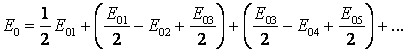
Din (7.116) rezulta ca toate parantezele sunt nule, si astfel putem scrie:
![]()
pentru ![]() impar, si
impar, si
![]() (7.119)
(7.119)
pentru ![]() par.
par.
Cum ![]() , putem considera
, putem considera ![]() , si astfel (7.118) si (7.119)
devin:
, si astfel (7.118) si (7.119)
devin:
![]() (7.120)
(7.120)
unde semnul " + " corespunde unui numar impar ![]() de zone Fresnel, iar semnul " - " corespunde unui
numar
de zone Fresnel, iar semnul " - " corespunde unui
numar ![]() par.
par.
Daca intre sursa I si
punctul P nu exista nici un ecran, atunci ![]()
![]() , si
, si ![]() , aceasta insemnand ca in
cazul unui front deschis al undei, amplitudinea rezultanta in punctul P este
jumatate din amplitudinea undei secundare emise de prima zona Fresnel, de pe ariea
, aceasta insemnand ca in
cazul unui front deschis al undei, amplitudinea rezultanta in punctul P este
jumatate din amplitudinea undei secundare emise de prima zona Fresnel, de pe ariea
![]() . Pentru
. Pentru ![]() si
si ![]() se obtine
se obtine ![]()
In concluzie, drept urmare a interferentei actiunea in punctul P a tuturor zonelor Fresnel, cu exceptia primei zone, se anuleaza reciproc, si totul se petrece ca si cum unda s-ar propaga din punctul I in punctul P prin interiorul unui canal ingust. Aceasta explica propagarea rectilinie a luminii, postulata in optica geometrica.
Expresia (7.115) fiind
simetrica fata de ![]() si
si ![]() , inseamna ca o sursa
punctiforma asezata in punctul P produce in I acelasi efect ca si in cazul cand
locul sursei I se inverseaza cu locul punctului de observatie P (aceasta
constituie principiul reversibilitatii
drumului razelor de lumina din optica geometrica).
, inseamna ca o sursa
punctiforma asezata in punctul P produce in I acelasi efect ca si in cazul cand
locul sursei I se inverseaza cu locul punctului de observatie P (aceasta
constituie principiul reversibilitatii
drumului razelor de lumina din optica geometrica).
Daca pe deschiderea
circulara de raza ![]() cade o unda plana,
cade o unda plana, ![]() , numarul zonelor Fresnel
este :
, numarul zonelor Fresnel
este :
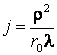 (7.121)
(7.121)
Dupa cum rezulta din (7.120),
intensitatea undei in punctul P este determinata de zonele Fresnel cu numarul 1
si ![]() , adica de
prima si ultima zona Fresnel. In functie de numarul
, adica de
prima si ultima zona Fresnel. In functie de numarul ![]() , ultima
zona poate fi importanta sau total neglijabila. Din (7.115) si (7.121) rezulta
ca numarul
, ultima
zona poate fi importanta sau total neglijabila. Din (7.115) si (7.121) rezulta
ca numarul ![]() este dat de trei parametri:
este dat de trei parametri: ![]()
![]() si
si ![]() . Variind acesti
parametri, vor apare maxime sau minime ale intensitatii intr-un punct din
spatiu.
. Variind acesti
parametri, vor apare maxime sau minime ale intensitatii intr-un punct din
spatiu.
Din calculele efectuate rezulta urmatoarele afirmatii:
a) Daca frontul undei este complet deschis, atunci intensitatea undei
intr-un punct P din spatiu este numai ![]() din intensitatea undei care ar fi data in
punctul respectiv numai de prima zona Fresnel.
din intensitatea undei care ar fi data in
punctul respectiv numai de prima zona Fresnel.
b) Daca aria deschiderii circulare, intr-un ecran opac, ar fi egala cu aria primei zone Fresnel, in punctul P s-ar obtine o intensitate de patru ori mai mare decat intensitatea undei cu frontul deschis.
c) Obturand toate zonele Fresnel pare (sau impare), amplitudinea rezultata este :
![]()
sau
![]()
adica intensitatea luminii in punctul P va fi mult mai mare decat daca lumina ar ajunge direct din I in P.
d) Schimband fazele tuturor zonelor pare (sau impare) cu ![]() , se poate obtine o
intensitate a luminii cu mult mai mare decat in cazul c).
, se poate obtine o
intensitate a luminii cu mult mai mare decat in cazul c).
Exemplul 5
Consideram difractia pe un
ecran circular cu diametrul de ![]() . Daca in
absenta ecranului intensitatea luminii in punctul de observatie P, venind de la sursa I (fig.23) are valoarea
. Daca in
absenta ecranului intensitatea luminii in punctul de observatie P, venind de la sursa I (fig.23) are valoarea ![]() pentru lungimea de unda
pentru lungimea de unda ![]() , se cer:
, se cer:
a) Intensitatea in centrul figurii de difractie, daca ecranul obtureaza prima zona Fresnel;
b) Intensitatea in centrul figurii de difractie, daca ecranul obtureaza jumatate din prima zona Fresnel;
c) Daca ecranul circular este plasat la jumatatea distantei ![]() dintre sursa si un ecran intunecos, pe care se
observa figura de difractie, sa se determine aceasta distanta, in conditiile de
la punctul a).
dintre sursa si un ecran intunecos, pe care se
observa figura de difractie, sa se determine aceasta distanta, in conditiile de
la punctul a).
Rezolvare
a) Din (7.112) obtinem:
![]() (7.122)
(7.122)
Din ![]() rezulta
rezulta ![]() ; introducand
in (7.122), expresia lui
; introducand
in (7.122), expresia lui ![]() ia forma:
ia forma:
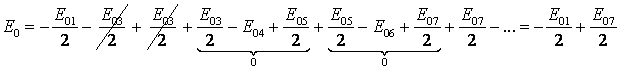 Asadar, pentru
Asadar, pentru ![]() numar par se obtine
numar par se obtine ![]() , iar
pentru
, iar
pentru ![]() numar impar se va obtine
numar impar se va obtine ![]() . Pentru un
numar infinit de zone
. Pentru un
numar infinit de zone ![]() , in ambele
situatii obtinem
, in ambele
situatii obtinem ![]() . In
consecinta, intensitatea undei in punctul de observatie va fi egala cu
intensitatea emisa de sursa in front deschis:
. In
consecinta, intensitatea undei in punctul de observatie va fi egala cu
intensitatea emisa de sursa in front deschis:
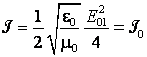
b)  pentru
pentru ![]() impar, respectiv
impar, respectiv
 pentru
pentru ![]() par (s-a considerat ca numarul de zone este
mare, astfel ca
par (s-a considerat ca numarul de zone este
mare, astfel ca ![]() , de unde
rezulta ca se poate considera ca
, de unde
rezulta ca se poate considera ca ![]() . Pentru
ambele cazuri se poate scrie
. Pentru
ambele cazuri se poate scrie ![]() , de unde
, de unde ![]() .
.
c) Raza primei zone Fresnel trebuie sa fie egala cu diametrul ecranului
circular, ![]() ,
, ![]() si
si ![]() . Din (7.115)
obtinem
. Din (7.115)
obtinem

de unde se obtine
![]()
7.5.3 Difractia Fraunhoffer (in lumina paralela)
Vom studia de difractia unei unde plane,
monocromatice, pe o fanta de latime ![]() si lungime
si lungime![]() . Vom
considera ca unda plana cade normal pe planul fantei (fig.24). Lentila L
focalizeaza lumina difractata sub diferite unghiuri
. Vom
considera ca unda plana cade normal pe planul fantei (fig.24). Lentila L
focalizeaza lumina difractata sub diferite unghiuri ![]() in diferite puncte ale ecranului E plasat in planul
focal al lentilei.
in diferite puncte ale ecranului E plasat in planul
focal al lentilei.
 Pentru efectuarea
calculelor vom diviza lungimea
Pentru efectuarea
calculelor vom diviza lungimea ![]() a fantei in benzi cu largimea elementara
a fantei in benzi cu largimea elementara ![]() , fiecare
banda
, fiecare
banda ![]() creand in punctul O o perturbatie de amplitudine:
creand in punctul O o perturbatie de amplitudine:
![]() (7.123)
(7.123)
Amplitudinea undei corespunzatoare intregii fante ![]() va fi data de:
va fi data de:
![]()
de unde obtinem:
![]() (7.125)
(7.125)
Distributia
fazelor in punctul O va fi aceeasi ca in planul AB, care face unghiul ![]() cu planul fantei. Tinand seama de faptul ca
raza ce ajunge pe fanta la distanta
cu planul fantei. Tinand seama de faptul ca
raza ce ajunge pe fanta la distanta ![]() de punctul A va parcurge o diferenta de drum
egala cu
de punctul A va parcurge o diferenta de drum
egala cu ![]() , diferenta de faza
corespunzatoare va fi
, diferenta de faza
corespunzatoare va fi ![]() , si astfel
se poate scrie:
, si astfel
se poate scrie:
![]()
Datorita coerentei perturbatiilor provenite de la
toate sursele elementare, de latime ![]() ,
amplitudinea undei rezultante in punctul O va fi :
,
amplitudinea undei rezultante in punctul O va fi :
 (7.127)
(7.127)
Astfel, amplitudinea
undei refractate sub unghiul ![]() este:
este:
 (7.128)
(7.128)
si intensitatea luminii care se propaga in urma difractiei sub unghiul ![]() va fi
va fi
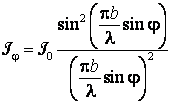 (7.129)
(7.129)
unde ![]() este intensitatea luminii care se propaga de pe intreaga
fanta pe directia
este intensitatea luminii care se propaga de pe intreaga
fanta pe directia ![]() . In unele cazuri
practice unghiul
. In unele cazuri
practice unghiul ![]() este suficient de mic, astfel ca
este suficient de mic, astfel ca ![]() , si
(7.129) ia forma:
, si
(7.129) ia forma:
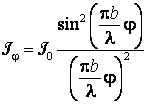 (7.129')
(7.129')
Se observa ca intensitatea luminii pe ecranul E variaza in functie de
unghiul ![]() (fig.25)
(fig.25)


Pentru directii care satisfac conditia:
![]() , (7.130)
, (7.130)
unde ![]() este egal cu
este egal cu ![]() ,
intensitatea luminii este 0. Deoarece
,
intensitatea luminii este 0. Deoarece ![]() , maximul
intensitatii se realizeaza pentru conditia
, maximul
intensitatii se realizeaza pentru conditia ![]() , si in
acest caz
, si in
acest caz ![]() .
.
Conditia de maxim secundar pentru
functia ![]() este
este  , de unde
obtinem:
, de unde
obtinem:
![]()
cu solutiile ![]() etc.
Valorile functiei
etc.
Valorile functiei ![]() pentru diferite valori ale lui
pentru diferite valori ale lui ![]() au fost indicate in tabelul 1.
au fost indicate in tabelul 1.
Maximele secundare au
intensitatea mult mai mica fata de cel principal. Astfel, cea mai mare parte a
energiei undei (peste 85%) este concentrata in maximul principal din fig.25,
adica in domeniul ![]() , sau
echivalent
, sau
echivalent ![]() . Deoarece
pozitia maximelor si minimelor depinde de lungimea de unda
. Deoarece
pozitia maximelor si minimelor depinde de lungimea de unda ![]() , figura de
difractie 25 este valabila numai pentru o lungime de unda data. Departarea
minimelor fata de centrul figurii creste o data cu micsorarea lui
, figura de
difractie 25 este valabila numai pentru o lungime de unda data. Departarea
minimelor fata de centrul figurii creste o data cu micsorarea lui ![]() , astfel ca
franja luminoasa centrala se largeste daca largimea fantei se micsoreaza.
Dimpotriva, crescand largimea fantei, pozitia primelor minime se apropie de
centrul figurii, iar maximul central devine mai pronuntat
, astfel ca
franja luminoasa centrala se largeste daca largimea fantei se micsoreaza.
Dimpotriva, crescand largimea fantei, pozitia primelor minime se apropie de
centrul figurii, iar maximul central devine mai pronuntat
Daca lumina nu este
monocromatica, pentru ![]() avem maxime principale
pentru toate lungimile de unda
avem maxime principale
pentru toate lungimile de unda ![]() . In cazul luminii albe,
in mijlocul figurii de difractie avem lumina alba, apoi benzi de diferite
culori: violet - cel mai apropiat de centrul figurii de difractie, si rosu -
cel mai indepartat de centrul figurii de difractie.
. In cazul luminii albe,
in mijlocul figurii de difractie avem lumina alba, apoi benzi de diferite
culori: violet - cel mai apropiat de centrul figurii de difractie, si rosu -
cel mai indepartat de centrul figurii de difractie.
7.5.4 Reteaua de difractie plana
Retelele de difractie plane, prin transmisie, se obtin
prin trasarea unor zgarieturi fine, drepte, paralele si echidistante pe
suprafata unor placi confectionate dintr-un dielectric transparent (fig.26)
Fantele de largime ![]() sunt separate prin portiuni opace de largime
sunt separate prin portiuni opace de largime ![]() , iar
marimea:
, iar
marimea:
![]() (7.131)
(7.131)
se numeste perioada (constanta) retelei. Pe retea cade normal un
fascicul de lumina monocromatica, coerenta, producandu-se un fenomen complex:
difractia luminii produsa de fiecare fanta si interferenta luminii provenita de
la toate fantele. Intensitatea undei deviate prin difractie de fiecare fanta sub
unghiul ![]() este data de (7.129). Diferenta de drum intre
fasciculele care trec printre doua fante vecine este
este data de (7.129). Diferenta de drum intre
fasciculele care trec printre doua fante vecine este ![]() , iar diferenta de faza
este:
, iar diferenta de faza
este:

![]()
Am ajuns astfel la problema interferentei fasciculelor multiple. Daca reteaua
este formata din ![]() fante, se poate scrie, pe baza formulei (7.89):
fante, se poate scrie, pe baza formulei (7.89):
 (7.133)
(7.133)
unde ![]() este intensitatea luminii obtinuta de la
fiecare fanta, in directia
este intensitatea luminii obtinuta de la
fiecare fanta, in directia ![]() . Primul termen din (7.133)
caracterizeaza distributia intensitatii luminii ca urmare a difractiei prin
fiecare fanta, iar al doilea distributia intensitatii datorita interferentei
luminii care trece prin cele
. Primul termen din (7.133)
caracterizeaza distributia intensitatii luminii ca urmare a difractiei prin
fiecare fanta, iar al doilea distributia intensitatii datorita interferentei
luminii care trece prin cele ![]() fante.
fante.


Pentru o diferenta de drum:
![]()
unde ![]() se numeste ordinul
de difractie pentru lungimea de unda specificata, avem maxime principale de interferenta. Daca este satisfacuta relatia (7.134),
expresia intensitatii luminii capata forma:
se numeste ordinul
de difractie pentru lungimea de unda specificata, avem maxime principale de interferenta. Daca este satisfacuta relatia (7.134),
expresia intensitatii luminii capata forma:
 (7.135)
(7.135)
Minimele intensitatii se
obtin cand numaratorul expresiei (7.133) se anuleaza, adica ![]() ,
,
de unde rezulta:
![]() (7.136)
(7.136)
unde ![]()
Maximele secundare se obtin din conditia ca derivata expresiei (7.133) in
raport cu ![]() sa se anuleze, de unde se obtine ecuatia
transcendenta:
sa se anuleze, de unde se obtine ecuatia
transcendenta:
![]() (7.137)
(7.137)
Solutia ecuatiei (7.137) este:
![]() (7.138)
(7.138)
unde ![]() .
.
Inlocuind valorile lui ![]() din (7.138) in (7.133), se obtin intensitatile
maximelor secundare in diferite puncte ale ecranului de observare. Astfel, distributia
intensitatii obtinuta prin interferenta a
din (7.138) in (7.133), se obtin intensitatile
maximelor secundare in diferite puncte ale ecranului de observare. Astfel, distributia
intensitatii obtinuta prin interferenta a ![]() fascicule este modulata de figura de difractie
in fiecare fanta (fig.27).
fascicule este modulata de figura de difractie
in fiecare fanta (fig.27).

La incidenta oblica (fasciculul incident nu este paralel cu normala la planul retelei), din fig.28 se observa ca pot aparea doua cazuri:
a) Cazul cand lumina cade pe retea pe o directie de aceeasi parte a normalei cu directia luminii difractate, si in formula (7.134) se va lua pentru diferenta de drum:
![]() (7.139)
(7.139)
b) Cazul cand lumina cade pe retea pe o directie de cealalta parte a normalei cu directia luminii difractate, si in formula (7.134) se va lua pentru diferenta de drum
![]() (7.140)
(7.140)
Exemplul 6
 Cunoscand lungimea de unda
Cunoscand lungimea de unda ![]() si distanta focala
si distanta focala ![]() a lentilei utilizate (fig.29), sa se determine,
pentru o retea cu constanta retelei
a lentilei utilizate (fig.29), sa se determine,
pentru o retea cu constanta retelei ![]() :
:
a) pozitiile maximelor de ordinul ![]()
![]() pentru o retea de difractie cu constanta
pentru o retea de difractie cu constanta ![]() ;
;
b) ordinul cel mai inalt al maximului care se mai poate observa cu reteaua data.
Rezolvare
a)
![]() (7.141)
(7.141)
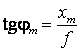 (7.142)
(7.142)
Eliminand ![]() intre (7.141) si (7.142), se obtine:
intre (7.141) si (7.142), se obtine:
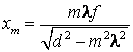 (7.143)
(7.143)
b) Conditia de ordin maxim se obtine din conditia ca numitorul relatiei (7.143) sa fie un numar real:
![]()
de unde:
![]() (7.144)
(7.144)
Exemplul 7
O sursa de lumina emite unde
cu lungimile de unda cuprinse intre ![]() si
si ![]() . Lumina
cade normal pe suprafata unei retele de difractie plane. Pentru o directie
. Lumina
cade normal pe suprafata unei retele de difractie plane. Pentru o directie ![]() a luminii difractate fata de directia luminii
incidente, cele doua lungimi de unda extreme ale spectrului se suprapun. Sa se
determine:
a luminii difractate fata de directia luminii
incidente, cele doua lungimi de unda extreme ale spectrului se suprapun. Sa se
determine:
a) Ordinul de difractie corespunzator suprapunerii celor doua lungimi de unda;
b) Numarul de trasaturi pe centimetru de retea;
c) Ordinul maxim de difractie ce se poate observa cu aceasta retea, pentru
lungimea de unda ![]() .
.
Rezolvare
a) 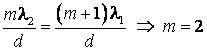 . Asadar,
pentru unda cu lungimea de unda
. Asadar,
pentru unda cu lungimea de unda ![]() ordinul de difractie este
ordinul de difractie este ![]() , in timp
ce pentru unda cu lungimea de unda
, in timp
ce pentru unda cu lungimea de unda ![]()
![]() .
.
b) Din ![]() sau
sau ![]() obtinem
obtinem 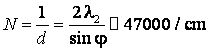
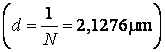
c) Conditia pentru ordinul maxim de difractie este:
![]()
de unde obtinem ![]() si astfel ordinul maxim este
si astfel ordinul maxim este ![]()
Exemplul 8
Sa se demonstreze ca cel mai
intens dintre maximele secundare din figura de difractie a unei retele de
difractie, ce contine un numar foarte mare ![]() de fante, nu depaseste
de fante, nu depaseste ![]() din valoarea maximelor principale.
din valoarea maximelor principale.
Rezolvare
Conditia de maxim secundar este data de (7.13 ):
![]()
Din transformari trigonometrice simple, obtinem:

In acest caz, (7.133) devine:
 (7.145)
(7.145)
Maximul
corespunzator pentru ![]() (maximul principal) va avea expresia:
(maximul principal) va avea expresia:
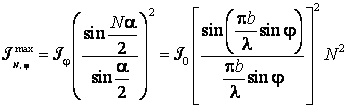 (7.146)
(7.146)
Maximul
secundar cel mai apropiat de cel mai apropiat de cel principal crespunde,
conform (7.138), lui ![]() :
:
![]()
Pentru un numar mare de
fascicule care interfera se considera ![]() si unghiul
si unghiul ![]() foarte mic, astfel ca se poate face
aproximatia
foarte mic, astfel ca se poate face
aproximatia ![]() si (7.145)
ia forma:
si (7.145)
ia forma:
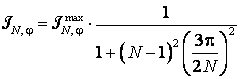 (7.147)
(7.147)
Deoarece
 si
si ![]() , (7.147)
devine:
, (7.147)
devine:

|