ELECTRODINAMICA SI TEORIA RELATIVITATII GRILE
Transformarile Lorentz speciale se obtin luand in considerare
a) invarianta etaloanelor de lungime si de timp
b) invarianta sarcinii electrice,
c) invarianta intervalului relativist, la schimbarea referentialului inertial.
Transformarile Lorentz speciale sunt transformarile coordonatelor unui eveniment la trecerea de la un sistem de referinta inertial la altul atunci cand
a) viteza relativa a celor doua sisteme de referinta este paralele cu una din axele sistemului de coordonate asociat reperului spatial,
b) viteza relativa a celor doua sisteme de referinta este paralela cu axa temporala,
c) viteza relativa a celor doua sisteme de referinta inertiale este orientata arbitrar in raport cu axele sistemului de coordonate asociat reperului spatial.
Transformarile Lorentz speciale sunt
a) transformari complexe,
b) transformari liniare,
c) transformari neliniare,
ale coordonatelor si timpului la scimbarea referentialului inertial.
Daca viteza relativa a celor doua sisteme de referinta inertiale este paralela cu axa Oz, se vor modifica, conform cu transformarile Lorentz speciale, urmatoarele coordonate ale unui eveniment:
a) x, z; b) z, y; c) z, t .
Simultaneitatea are un caracter relativ in teoria relativitatii restranse datorita:
a) principiului actiunii la distanta,
b) principiului constantei vitezei luminii in vid,
c) principiului ireversibilitatii sensului timpului.
Lungimea proprie este
a) lungimea geometrica,
b) lungimea cinematica,
c) lungimea etalonului.
Formula contractiei lungimii este:
a)![]() ; b)
; b)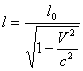 ; c)
; c) ![]() ,
,
unde l0 este lungimea proprie.
Formula dilatarii duratei este:
a) ![]() ; b)
; b) ![]() ; c)
; c) 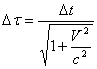 ;
;
unde Δτ este intervalul de timp propriu
Pentru masurarea intervalului de timp propriu este necesar
a) un sistem de ceasuri sincronizate,
b) un singur ceas,
c) un sistem de coordonate cartezian.
Legea relativista de compunere a vitezelor se poate stabili plecand de la
a) transformarile de faza,
b) transformarile Galilei,
c) transformarile Lorentz.
Formula relativista de transformare a componentei x a vectorului viteza a unei particule, la trecerea de la un sistem de referinta inertial la altul, cand viteza relativa V a acestor sisteme este paralela cu axa Oy, este:
a) 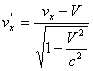 ; b)
; b) 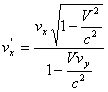 ; c)
; c) 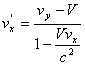 .
.
Formulele relativiste de transformare ale componentelor vectorului acceleratie la schimbarea referentialului inertial indica:
a) invarianta acestor componente,
b) dependenta stricta a fiecarei componente a acceleratiei dintr-un sistem de referinta inertial de aceleasi componente din celalalt sistem de referinta,
c) dependenta unei componente a acceleratiei dintr-un sistem de referinta inertial si de alte componente ale acceleratiei din celalalt sistem de referinta inertial.
|