Ecuatia fundamentala a dinamicii relativiste. Cuadrivectorul forta-putere

Ecuatia fundamentala a dinamicii relativiste. Cuadrivectorul forta-putere

Am aratat ca scrierea relativist-invarianta a legilor fizicii implica trecerea de la vectorii in spatiul tridimensional la cuadrivectorii in spatiul 222h72c Minkowski. Daca notam cu timpul propriu ( in formula 4.43) obtinem:

_,

sau

(4.91)

unde este diferentiala timpului propriu, iar este diferenti­ala timpului in raport cu sistemul de referinta aflat in repaus.

Se definesc componentele cuadrivectorului prin formulele:

si in mod explicit:

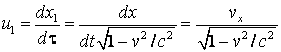(4.93)

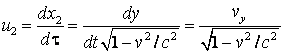(4.94)

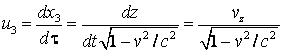(4.95)

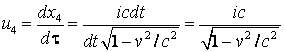(4.96)

Din se obtine invarianta modulului cuadrivectorului viteza:

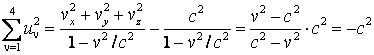(4.97)

Se defineste cuadrivectorul acceleratie pe componente astfel:

(4.98)

In teoria relativitatii restrinse se arata ca masa particule­lor depinde de viteza dupa formula:

(4.99)

Nu ne vom ocupa de rationamentele care conduc la formula (4.99). Este suficient ca, asa cum am aratat in capitolul precedent datele experimentale confirma valabilitatea acestei formule.

In mecanica Newtoniana legea fundamentala (sau legea a doua) este:

(4.100)

Se arata ca legea fundamentala a dinamicii ramane valabila sub aceasta forma si in cadrul TRR. Formula (4.100) poate fi scrisa pe componente:

, sau ,

de unde

(4.101)

Analog obtinem formulele:

(4.102)

(4.103)

Marimile si reprezinta primele 3 componente ale cuadrivectorului forta Minkowski. Analog introducem a patra componenta a acestui cuadrivector:

(4.104)

Forma explicita a lui se afla daca inmultim relatiile (4.101) - (4.104) respectiv cu si , iar apoi le adunam:

Tinand seama de egalitatea , obtinem:

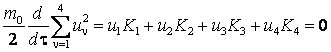(4.106)

Am utilizat (4.97), care indica faptul ca patratul cuadrivectorului viteza este constant, si derivata sa in raport cu timpul propriu va fi nula. Din (4.106) obtinem:

 

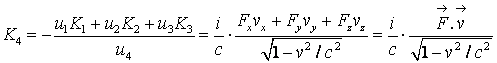
Asadar, formulele (3.100) - (3.104) pot fi scrise sub forma:

(4.108)

sau

, (4.109)

de unde

unde

Formulele (4.108) - (4.110) reprezinta expresiile ecuatiei fundamentale a dinamicii relativiste, fiind analoage cu ecuatia fundamentala a mecanicii Newtoniene in spatiul tridimensional.

(4.111)

unde , corespunzator coordonatelor .

Cuadrivectorul forta are componentele:

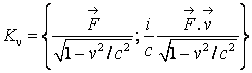(4.112)

Introducem cuadrivectorul impuls:

sau

(4.113)

Astfel, formula fundamentala a dinamicii relativiste poate fi scrisa si sub forma:

(4.114)

Forma relativista a ecuatiei fundamentale a dinamicii este invarianta fata de transformarile Lorentz.