Cuprins:
1. Generalitati
2. Variatia tensiunilor cu inclinarea sectiunii. Tensiuni principale si directii principale
3. Reprezentarea grafica a variatiei tensiunilor prin cercul lui Mohr
4. Cazuri particulare ale starii plane de tensiune
5. Legea lui Hooke generalizata in cazul starii plane
6. Expresia generala a energiei de de 848b15i formatie pentru starea plana
1. Generalitati
Pentru studiul teoriilor de rezistenta a materialelor si al solicitarilor compuse, precum si al altor probleme de rezistenta a materialelor, este necesara cunoasterea unor aspecte de baza ale teoriei elasticitatii. Se va analiza numai cazul starii plane de tensiuni, caz particular de solicitare, foarte des intalnit in aplicatii. Principalele probleme pe care le trateaza teoria elasticitatii se vor analiza in continuare.
2. Variatia tensiunilor cu inclinarea sectiunii. Tensiuni principale si directii principale
In cazul solicitarilor studiate pana in prezent, fortele erau aplicate in planul median al barelor (planul xOy), fiind deci coplanare si in echilibru. Starea de solicitare realizata se numeste plana, intrucat solicitarea este identica in plane paralele cu planul median.
Daca grosimea grinzii este relativ mica, sub actiunea fortelor aplicate se produc tensiuni coplanare cu fortele date, iar starea de solicitare este o stare plana de tensiuni.
Cazurile de stari plane studiate sunt:
1) intinderea sau compresiunea centrica, unde fortele axiale N, produc tensiuni normale s, in sectiunea transversala. Un element dreptunghiular OBCD de grosime unitara va fi solicitat de tensiuni normale s (figura 1.a);
2)
forfecarea, unde fortele taietoare T
produc tensiuni tangentiale![]() , in planul sectiunii transversale. Un
element dreptunghiular OBCD va fi supus la forfecare de tensiuni
, in planul sectiunii transversale. Un
element dreptunghiular OBCD va fi supus la forfecare de tensiuni ![]() (figura 1.b) ;
(figura 1.b) ;
3) incovoierea, in care eforturile sectionale M si T
produc tensiunile s si ![]() . Un element dreptunghiular va fi
solicitat de tensiunile s si
. Un element dreptunghiular va fi
solicitat de tensiunile s si ![]() (figura 1.c).
(figura 1.c).
In cazul mai general al starii
plane, ce nu va fi studiat, un element OBCD este solicitat de tensiunile s ![]() si
si ![]() figura 1.d) .
figura 1.d) .

Se va studia cazul in care in sectiunea
transversala a barei apar tensiunile s si ![]() (figura 1.c). Se pune problema determinarii
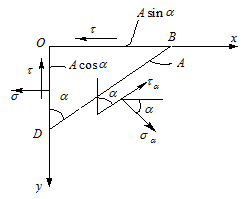
tensiunilor pe o suprafata inclinata cu unghiul a fata de latura OD, (figura 2).
(figura 1.c). Se pune problema determinarii
tensiunilor pe o suprafata inclinata cu unghiul a fata de latura OD, (figura 2).
Tensiunile care se dezvolta pe
aceasta fata inclinata se noteaza cu s![]() si
si ![]()
Scriind conditiile de echilibru ale elementului triunghiular OBD, de
grosime egala cu unitatea, rezulta (considerand ca suprafata BD are aria A):

sau :
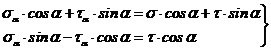
Rezolvand
sistemul in raport cu necunoscutele s![]() si
si![]()
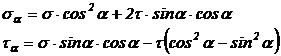
dar

![]() (1)
(1)
![]() (2)
(2)
Relatiile (1) si (2) permit calculul
tensiunilor s![]() si
si![]() pentru orice sectiune inclinata cu
unghiul a
pentru orice sectiune inclinata cu
unghiul a
Pe anumite
directii, numite directii principale de solicitare, tensiunile normale ![]() au valori maxime sau minime, numite tensiuni
principale.
au valori maxime sau minime, numite tensiuni
principale.
Conditia de extremum este:
![]()
![]() (3)
(3)
Ecuatia trigonometrica (3) are doua solutii, corespunzator celor doua
directii principale, ![]() si
si ![]() intre care exista relatia
intre care exista relatia ![]() , sau
, sau
![]() , (4)
, (4)
ceea ce arata ca directiile
principale (1) si (2), date de unghiurile a![]() si a
si a![]() sunt
sunt
perpendiculare.
Pe una din directii tensiunea s este maxima, pe cealalta minima.
Se constata ca:
![]()
deci pe directiile principale,
tensiunile tangentiale![]() sunt nule, deci pe astfel de sectiuni
se produce o stare biaxiala de intindere si compresiune.
sunt nule, deci pe astfel de sectiuni
se produce o stare biaxiala de intindere si compresiune.
Tensiunile principale, notate ![]() si
si ![]() vor fi obtinute inlocuind in relatia (1) unghiul 2a dat de relatia (3).
vor fi obtinute inlocuind in relatia (1) unghiul 2a dat de relatia (3).
Stiind ca:
![]()
se obtin valorile tensiunilor principale,
![]() (5)
(5)
Considerand
semnul plus rezulta tensiunea maxima ![]() ; tensiunea minima,
; tensiunea minima, ![]() , se obtine considerand semnul minus
din relatia (5) .
, se obtine considerand semnul minus
din relatia (5) .
Adunand ![]() si
si ![]() se obtine:
se obtine:
![]()
ceea ce arata ca suma tensiunilor normale pe doua plane ortogonale este un invariant, adica nu depinde de unghiul a
Pentru a obtine directiile dupa care
tensiunile tangentiale ![]() sunt maxime este necesar ca:
sunt maxime este necesar ca:
![]() = 0 sau s cos 2a
= 0 sau s cos 2a ![]() sin 2a
sin 2a
cu solutia
![]() (6)
(6)
Se obtin doua
valori pentru unghiurile ![]()
![]()
![]() , (7)
, (7)
deci cele doua directii dupa care tensiunile ![]() sunt extreme, sunt
ortogonale. Liniile in lungul carora tensiunile
sunt extreme, sunt
ortogonale. Liniile in lungul carora tensiunile ![]() sunt maxime se numesc linii
de lunecare.
sunt maxime se numesc linii
de lunecare.
Din relatia (6) rezulta:
![]()
ceea ce exprima conditia de ortogonalitate intre unghiurile 2a si 2a . Prin urmare:
a a ![]() ,sau
,sau
a a ![]() (8)
(8)
Asadar
liniile de lunecare, dupa care apar tensiuni tangentiale maxime, sunt inclinate
cu 45![]() fata de directiile principale.
fata de directiile principale.
Pentru
aflarea tensiunilor tangentiale maxime, se inlocuieste expresia (6) in (2).
Rezulta tensiunile maxime, ![]() si
si ![]()
![]()
![]() (9)
(9)
sau, tinand seama de relatia (5):
![]() (10)
(10)
Cele doua tensiuni tangentiale maxime sunt egale si de semn contrar, ceea ce confirma legea dualitatii tensiunilor tangentiale.
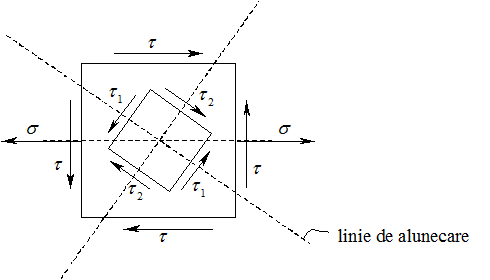
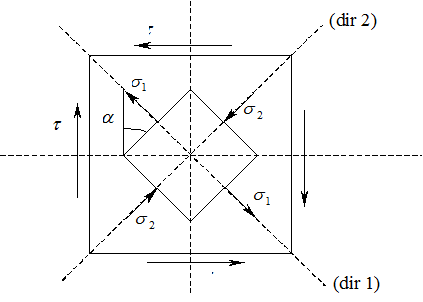
In mod practic, pentru determinarea directiei principale (1), se tine seama ca aceasta este cuprinsa intre diagonala intinsa a elementului solicitat si directia dupa care tensiunile normale sunt maxime, in valoare algebrica.
In figura 3, directia principala (1) se afla in zona hasurata.

Pentru elementul din figura se cunosc
tensiunile: s = 60 N/mm

![]()
![]() = - 30 N/mm
= - 30 N/mm![]() . Se cer directiile principale,
tensiunile principale, liniile de alunecare, tensiunile tangentiale maxime
(figura 4).
. Se cer directiile principale,
tensiunile principale, liniile de alunecare, tensiunile tangentiale maxime
(figura 4).
Rezolvare:
tg 2a =![]()
a![]() = - 45 ; 2a
= - 45 ; 2a![]() = - 45
= - 45
a![]() = - 22 30’ ; a
= - 22 30’ ; a![]() = -22
= -22
![]()
![]()
![]()
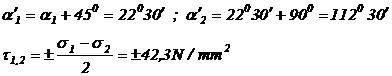
3. Reprezentarea grafica a variatiei tensiunilor prin cercul lui Mohr
Variatia
tensiunilor cu inclinarea sectiunii, ce trece printr-un punct, se poate reprezenta intr-un
sistem de referinta cu coordonatele s si ![]() . Pentru aceasta se elimina
parametrul 2a intre relatiile (1) si (2).
. Pentru aceasta se elimina
parametrul 2a intre relatiile (1) si (2).

Din relatia(5) rezulta:
![]()
deci:
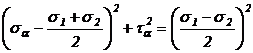 (11)
(11)
Ecuatia (11)
este ecuatia unui cerc cu centrul in punctul C ![]() si avand raza R =
si avand raza R = ![]() (figura 6).
(figura 6).

4. Cazuri particulare ale starii plane de tensiuni
Particularizand schema din cazul starii plane generale studiata si utilizand formulele obtinute, se pot gasi cazurile particulare de stari plane de tensiuni, studiate in cadrul solicitarilor simple.
a) Starea liniara de tensiuni (intinderea sau compresiunea centrica)
Daca in formulele (1), (2),
(3), (5), (10) se considera ![]() = 0, se gaseste cazul starii liniare de intindere sau
compresiune, in care:
= 0, se gaseste cazul starii liniare de intindere sau
compresiune, in care:
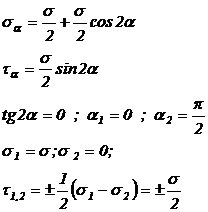
b) Forfecarea pura
In formulele stabilite in paragraful anterior, considerand s , rezulta:
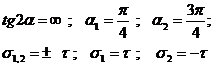
Situatia este prezentata in figura 7.
5. Legea lui Hooke generalizata, in cazul starii plane
Se cunoaste legea lui Hooke pentru starea liniara de tensiuni (figura 8):
![]()
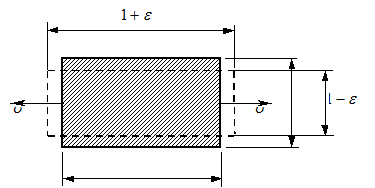
Deformatia transversala are expresia:
![]()
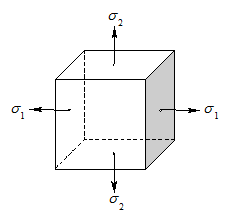
Fie un
element de volum unitar, pe fetele caruia actioneaza tensiunile principale s![]() , respectiv s
, respectiv s![]()
Tensiunea s![]() produce o alungire e
produce o alungire e![]() , pe directia principala (1),
respectiv o scurtare specifica e
, pe directia principala (1),
respectiv o scurtare specifica e![]() pe directia principala (2), si e
pe directia principala (2), si e![]() pe directia principala (3):
pe directia principala (3):

![]()
Tensiunea s![]() produce o alungire pe directia (2),
egala cu e
produce o alungire pe directia (2),
egala cu e![]() , respectiv o scurtare pe directia
(1), e
, respectiv o scurtare pe directia
(1), e![]() si o scurtare specifica pe directia (3),
si o scurtare specifica pe directia (3), ![]() (figura 9):
(figura 9):

Daca actioneaza simultan cele
doua tensiuni principale, deformatia
specifica totala se obtine prin insumarea
efectelor:
Figura 9
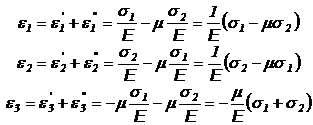 (12)
(12)
Daca in
locul directiilor principale (1) si (2) se considera directiile axelor x, y si z, se obtin relatiile analoage:  (13)
(13)
Daca axele x si y nu sunt directii principale, deci exista si tensiuni tangentiale
![]() =
= ![]() , lunecarile specifice sunt:
, lunecarile specifice sunt:
![]() (14)
(14)
Relatiile (13) si (14) sau (12) exprima legea lui Hooke generalizata in cazul starii plane de tensiuni.
Se
observa ca starii plane de tensiuni ii corespunde o stare spatiala de deformatii,
intrucat![]()
Rezolvand
primele doua relatii (13) in raport cu s![]() si s
si s![]() rezulta:
rezulta:
![]() (15)
(15)
Daca axele x si y sunt axe principale, relatiile (15) devin:
![]() (16)
(16)
6. Expresia generala a energiei de de 848b15i formatie pentru starea plana
Se considera
un element de volum egal cu unitatea,
supus la tensiunile principale s![]() si s
si s![]()
Sub actiunea
tensiunilor s![]() si s
si s![]() se produc deformatiile e
se produc deformatiile e![]() , respectiv e
, respectiv e![]() pe directiile (1) si (2).
pe directiile (1) si (2).
Lucrul mecanic corespunzator elementului considerat, dupa cum s-a vazut si in capitolele precedente, este (figura 10):
![]()
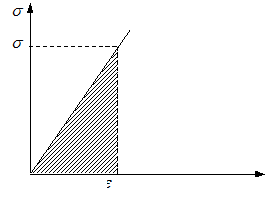
Datorita
deformatiei elementului de volum, lucrul mecanic datorat tensiunilor s![]() este:
este:
![]()
iar cel datorat tensiunilor s![]() este:
este:
![]()
Lucrul mecanic elementar pe unitatea de volum va fi:
![]()
Tinand seama de relatiile (12) rezulta:
![]() , sau
, sau
![]() (17)
(17)
Aceasta energie are doua efecte, asupra volumului elementului, unul de variatie a volumului si al doilea de variatie a formei acestuia.
Energia de deformatie a unui corp de volum V este:
W = ![]() (18)
(18)
In cazul
barelor, se obisnuieste ca energia potentiala de deformatie sa se exprime in
functie de eforturile din sectiune.I ¥n cazul in care in sectiunea barei apar
eforturile ![]() , energia potentiala de deformatie este egala cu suma energiilor produse
de cele trei eforturi (energia de deformatie produsa de forta taietoare T se poate neglija , fiind mica in
raport cu energia de deformatie produsa de celelalte eforturi).
, energia potentiala de deformatie este egala cu suma energiilor produse
de cele trei eforturi (energia de deformatie produsa de forta taietoare T se poate neglija , fiind mica in
raport cu energia de deformatie produsa de celelalte eforturi).
Deci, pentru o bara de lungime l se poate scrie:
W = 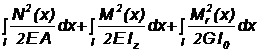 .
.
|