Energia oscilatorului liber
Pentru un sistem aflat in miscare oscilatorie, energia depinde attt de viteza de oscilatie cat si de pozitia relativa a corpului care oscileaza fata de pozitia de echilibru. Expresia energiei totale a sistemului are un termen cinetic si un termen poten&# 646e48g 355;ial.
Energia cinetica are expresia:
(3.4.40)
In cazul unui oscilator liniar, liber, neamortizat, elongatia si viteza variaza in timp conform relatiilor (3.1.1) si (3.1.6) astfel incat energia cinetica a acestuia este:
(3.4.41)
Energia potentiala a acestui oscilator este:
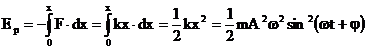(3.4.42)
tinand cont de relatia 
.
Energia totala a oscilatorului devine atunci:
(3.4.43)
Se analizeaza in continuare ce se intampla cu energia totala a oscilatorului liber, atunci cand el este neamortizat si atunci cand el este amortizat.
Energia oscilatorului liber neamortizat
Pornind de la
ecuatia diferentiala a miscarii oscilatorii, data
de relatia (3.4.2), prin inmultire cu 
, se obtine: 
(3.4.44)
Aceasta ecuatie mai poate fi scrisa si sub forma:
(3.4.45)
sau tinand cont de relatia (3.4.43) se obtine:
(3.4.46)
adica, in cazul oscilatiilor libere neamortizate, energia totala a oscilatorului este constanta.
Din relatia (3.4.43) se observa ca energia totala a oscilatorului depinde numai de constanta elastica a elementului elastic, k si de amplitudinea oscilatiei,A.
Energia oscilatorului liber amortizat
Se considera cazul
oscilatorului liber amortizat, cu miscare subcritica. Daca
ecuatia diferentiala a oscilatorului liber amortizat (3.4.14) se
inmulteste cu , se obtine: 
(3.4.47)
sau: 
(3.4.48)
Deci, in cazul oscilatorului liber amortizat:
(3.4.49)
unde dLv este lucrul mecanic elementar efectuat de fortele de frecare vascoasa asupra sistemului.
Se observa ca energia totala a oscilatorului liber amortizat scade, datorita pierderilor energetice sub forma lucrului mecanic al fortelor de frecare.
Pornind de la ecuatia de miscare a oscilatorului liber amortizat, descrisa de relatia (3.4.23), se poate calcula scaderea in timp a energiei acestuia.
Daca la un anumit
moment de timp energia totala a oscilatorului este 
atunci tinand cont de relatia (3.4.23) se
obtine:
(3.4.50)
Energia totala a oscilatorului la momentul de timp t este:
(3.4.51)
Dupa o pseudoperioada, energia totala a oscilatorului liber amortizat este:
(3.4.52)
Facand raportul celor doua energii la doua momente de timp ce difera intre ele printr-o pseudoperioada, se obtine:
(3.4.53)
in care 
este decrementul logaritmic al oscilatiei.
Deci, energia totala a oscilatorului liber amortizat (cazul miscarii subcritice) scade exponential in timp, datorita pierderilor energetice, sub forma de lucru mecanic al fortelor de frecare.
|
