Fizica nucleara si particule elementare
Capitolul al V-lea
I.5.1. Sa se stabileasca relatia care da numarul de nuclee radioactive produse la iradierea cu neutroni termici a unei cantitati dintr-un izotop dat daca se admite ca:
(i) numarul de nuclee radioactive produse este proportional cu marimea fluxului de neutroni, Φ si cu numarul de nuclee iradiate, existente in unitatea de volum;
(ii) numarul de nuclee radioactive formate intr-un interval de timp dt este proportional cu durata acestui interval;
(iii) nucleele radioactive formate se dezintegreaza in timp conform legii dezintegrarii radioactive.
I.5.2. Sa se determine timpul de iradiere cu un flux de neutroni, Φ, pentru o proba de masa m dintr-un element cunoscut pentru a se obtine o activitate Λ.
Se considera urmatoarele regimuri de functionare a reactorului: (a) functionare continua;
(b) functionare zilnica de 12 ore.
Se cunosc abundenta izotopica, a, sectiunea eficace, σ,
timpul de injumatatire 
.
I.5.3. Sa se scrie reactia de fuziune nucleara dintre doua nuclee de deuteriu. Calculati energia eliberata in aceasta reactíe nucleara. Se cunosc masele atomice ale nucleelor implicate, anume: Hidrogen 1.007825 u, Deuteriu 2.014 102 u, Tritiu 3,016 049 u. Se dau: 1 u = 1.66x10-27 kg, c = 3x108 m/s.
Se cere prezentarea rezultatului in unitatea de masura din Sistemul International, precum si in o unitate de masura din Sistemul natural (tolerat).
I.5.4. Atunci cand un nucleu de deuteriu fuzioneaza cu un nucleu de tritiu se obtine un nucleu de heliu si un neutron. Energia eliberata este de 2.88x10-12 J.
(a) Sa se scrie ecuatia reactiei.
(b) Sa se calculeze masa heliului produs.
Se dau: masa deuteriului (3.345x10-27 kg), masa tritiului (5.008x10-27 kg), masa neutronului (1.675x10-27 kg) si viteza luminii in vid (3x108 m/s).
I.5.5. Un nucleu de uraniu este continut intr-un tub de dimensiuni apropiate. Atomul de uraniu strabate tubul cu o viteza relativa in raport cu acesta de 5.00x105 m/s si se dezintegreaza in kripton (Kr) si bariu (Ba). Nucleul de kripton este emis inapoi cu o viteza de 2.35x106 m/s relativa la cea a bariului, dupa separare. Care este viteza nucleului de kripton relativa la tubul care il contine
Se face ipoteza ca nu sunt emise alte particule. Se cunosc numerele de masa ale nucleelor implicate, anume: 235 (U), 95 (Kr), 140 (Ba).
I.5.6. Sectiunea
eficace de fisiune a uraniului natural sub actiunea neutronilor termici este de
4.22 b. Se cere sa se calculeze sectiunea eficace de fisiune a izotopului 
,
cunoscand compozitia izotopica a uraniului natural, anume: 
,
,
.
Un flux de neutroni termici 
cade pe o tinta subtire de uraniu natural. Sa
se evalueze cate acte de fisiune se produc intr-o secunda, daca grosimea tintei
este 
.
Se da densitatea uraniului natural: 
.
I.5.7. Un fascicul de particule α cade pe o
tinta groasa de aluminiu. Particulele α au energia cinetica 
,
iar parcursul lor masic mediu in aluminiu este 
.
Se cer urmatoarele:
(a) scrierea ecuatiei reactiei, stiind ca unul din produsii de reactie este protonul;
(b) calcularea sectiunii eficace medie de reactie, daca se determina experimental ca 8 protoni sunt produsi pentru fiecare milion de particule α incidente.
Se cunoaste densitatea aluminiului: 
.
I.5.8. Un accelerator
de ioni grei furnizeaza un fascicul de ioni de 
cu energia cinetica de 20 MeV. Sa se analizeze posibilitatea investigarii reactiei urmatoare:
stiind ca aceasta este o reactie endoterma, iar caldura de reactie
necesara este: 
.
I.5.9. Pe o tinta de 
cade un fascicul de neutroni cu energia de 5 MeV. Sa se calculeze sectiunea eficace absoluta pentru capturarea
neutronilor de nucleele tinta de in ipoteza ca neutronul este un obiect
punctual, iar ciocnirea dintre neutron si nucleu este una de "atingere"
("grazing").
I.5.10. Pentru o reactie nucleara endoenergetica (endotermica) la energii joase, cu doi produsi de reactie in starea finala, sa se calculeze energia de prag. Se considera cunoscute marimile fizice caracteristice tuturor nucleelor implicate in reactie.
I.5.11. Un fascicul de
neutronii cu energii cinetice sub 1 MeV se
imprastie izotrop, in sistemul centrului de masa, pe nuclee cu numar de masa A. Sa se arate ca energia medie pierduta pe ciocnire, mediata pe multe
ciocniri, este o fractie 
din energia cinetica a neutronilor incidenti.
I.5.12.
Sa se calculeze care este fractiunea din energia cinetica initiala pe care o
pierde un neutron prin ciocnirea sa elastica si centrala cu un nucleu de 
aflat in repaus.
I.5.1. Numarul de nuclee activate in unitatea de timp, in ipotezele incluse in enuntul problemei, se poate calcula luand in considerare atat procesul de activare cu neutroni, cat si pe cel de dezintegrare a unora dintre nucleele radioactive formate. Se poate scrie urmatoarea ecuatiei diferentiala:
Pentru rezolvare se procedeaza la separarea variabilelor in ecuatia diferentiala de mai sus. Se obtine:
Ecuatia
diferentiala se poate rezolva prin mai multe metode. Se poate alege urmatoarea
metoda: se inmulteste relatia de mai sus cu 
;
se obtine:
Se constata ca membrul stang al relatiei se poate pune sub forma urmatoare:
De aceea, ecuatia diferentiala anterioara se poate scrie astfel:
de unde rezulta
Se integreaza aceasta ecuatie si se obtine:
ceea ce era de demonstrat
Nota Notatia consacrata este q.e.d. si provine din limba latina (q.e.d. = quot erat demonstrandum).
I.5.2. (a) Se pleaca de la expresia obtinuta anterior, pentru numarul de nuclee radioactive obtinute in proba dupa un timp de iradiere ta, anume:
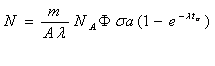
Se calculeaza activitatea probei radioactive astfel:
.
Se stabileste
activitatea initiala a probei
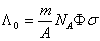
Din relatiile anterioare se determina timpul de activare ta pentru functionarea continua a reactorului:
si se obtine expresia:
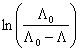
sau, detaliind pentru datele initiale ale problemei:
ln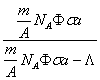
(b) Fie 
fractia dintr-o zi in care functioneaza
reactorul. Activitatile probei, dupa fiecare perioada de functionare se pot
scrie astfel:
De aici se obtine expresia timpului de activare pentru acest regim de functionare a reactorului:
I.5.3. Reactia de fuziune nucleara dintre doua nuclee de deuteriu se scrie astfel:
Caldura de reactie se scrie astfel:
Valoarea acestei calduri de reactiei este urmatoarea:
Valoarea caldurii de reactie, in Sistemul natural, este:
I.5.4. (a) Ecuatia reactiei este:
sau
unde Q este energia eliberata
(b) Calculul energiei eliberate in reactie se face pe baza relatiei de mai jos:
de unde se obtine:
Efectuand calculele numerice se obtine: 
I.5.5.
Fie 
viteza
relativa a kriptonului si fie 
viteza
relativa a bariului in raport cu tubul, pe directia inapoi, respectiv, pe
directia inainte. Se noteaza cu 
viteza relativa a kriptonului in raport cu cea
a bariului, dupa separare.
Pe baza geometrie procesului de separare, se poate scrie urmatoarea relatie intre cele trei viteze:
(1)
Legea conservarii impulsului permite scriere urmatoarei relatii:
(2)
sau
(3)
Se formeaza un sistem de ecuatii din ecuatia (1) si ecuatia (3), anume:
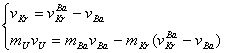(4)
Se rezolva sistemul si se obtine:
(5.1)
respectiv,
(5.2)
Valorile celor
doua viteze sunt: 
,
respectiv, 
I.1.5.6. Cum sectiunea eficace de fisiune totala pentru uraniul natural este o medie ponderata pe izotopii constituenti, ponderea fiind data de abundentele lor izotopice, se poate scrie relatia:
Pentru izotopul
de valoarea sectiunii eficace de fisiune cu
neutroni termici se poate scrie, avand in vedere notatiile din enunt:
Introducand valorile numerice, se obtine:
Pentru determinarea numarului de
acte de fisiune produse intr-o secunda se ia in considerare fluxul neutronilor
termici, sectiunea eficace de fisiune a uraniului natural sub actiunea
neutronilor termici, grosimea tintei, precum si numarul de nuclee pe unitatea
de volum, 
. Se poate scrie o relatie de forma urmatoare:
Numarul de
nuclee pe unitatea de volum, ,
se determina cu ajutorul relatiei de mai jos:
unde 
este numarul lui Avogadro, ρ este
densitatea uraniului natural, iar A masa atomica a uraniului natural, ponderata
pe izotopi.
Expresia numarului de fisiuni produse intr-o secunda se poate scrie astfel:
Valoarea numerica care se obtine este:
I.5.7. (a) Ecuatia reactiei se scrie astfel:
Din tabelul de
radionuclizi se obtine ca elementul 
este un izotop al siliciului.
(b) Sectiunea eficace medie se poate determina folosind o expresie de forma:
de unde rezulta: 
;
Scriind
legea de atenuare a fascicolului:
obtinem:
Atunci
vom avea: 
sau 
Expresia
lui s devine:
I.5.8. Reactia considerata:
este o reactie
endoterma, iar caldura de reactie este:
.
De aceea, este necesar sa se analizeze daca energia cinetica de 20 MeV a fasciculului de ioni de este suficienta, adica asigura energia de prag pentru producerea reactiei.
Se stie ca, pentru ciocnire cu doi produsi de reactie in starea finala
(
)
energiile cinetice in sistemul centrului de masa (SCM) trebuie sa indeplineasca
conditia urmatoare:
Energia cinetica a nucleului
proiectil, in SCM, 
,
este mai mica decat energia cinetica a nucleului proiectil, 
,
in sistemul laboratorului (SL), deoarece nucleul tinta este in repaus si 
.
Energia cinetica totala in SCM se mai poate scrie:
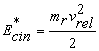(1)
unde 
este masa redusa a nucleelor care se ciocnesc,
iar 
este viteza relativa a acestora, indiferent de
sistemul de referinta; pentru experimente cu tinta fixa este viteza nucleului
proiectil in raport cu nucleul tinta.
In ipoteza considerata, anume ca nucleul tinta este in repaus in SL, energia cinetica totala este data de relatia de mai jos:
(2)
Folosind ecuatiile (1) si (2) se poate scrie urmatoarea relatie de legatura:
(3)
Pentru
producerea reactiei este necesar ca 
.
Se poate estima energia de prag, astfel:
Se efectueaza calculele si se obtine:
Se constata
faptul ca 
. De aceea, reactia considerata nu se poate
produce (nu se poate deschide canalul de reactie mentionat).
I.5.9. Pentru calcularea sectiunii eficace absolute, in conditiile unei reactii de "atingere", se poate folosi relatia urmatoare:
Deoarece, 
si 
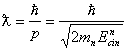, relatia anterioara se mai poate scrie sub
forma de mai jos:
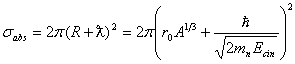
Efectuand calculele se obtine:
deoarece
I.5.10. Fie reactia nucleara de mai jos:
Nucleul incident
(proiectil) P, de masa 
,
se deplaseaza cu viteza 
si cade pe nucleul tinta T, masa 
,
aflat in repaus (
).
In urma procesului de interactie dintre cele doua nuclee se produc doua nuclee,
de mase 
si 
,
emise la unghiul 
,
respectiv, la unchiul 
,
cu viteze 
,
respectiv, 
.
Cele doua unghiuri sunt masurate in raport cu directia initiala de miscare a
nucleului incident.
Formele generale ale legii conservarii impulsului si legii conservarii energiei totale se scriu astfel:
(1)
(2)
Luand in
considerarea faptul ca nucleul tinta este in repaus, precum si faptul ca
energia totala se poate scrie ca suma dintre energia de repaus, 
,
si energia cinetica, 
,
cele doua ecuatii anterioare se pot rescrie astfel:
(3)
(4)
Caldura de reactie se defineste, luand in considerare balanta energetica, astfel:
(5)
Folosind aceasta expresie in relatia (4) se poate scrie:
(6.1)
sau
(6.2)
Pentru energii cinetice mici, se pot folosi relatiile de legatura clasice dintre energia cinetica si impuls, anume:
(7)
Ecuatia (3) se poate scrie pe componente, in plan. Se obtin relatiile de mai jos:
(8.1)
(8.2)
Pe baza relatiilor (6.2), (7), (8.1) si
(8.2), expresia caldurii (energiei) de reactie se poate scrie in modul urmator,
eliminand marimile produsului de reactie 
asociat
nucleului rezidual:
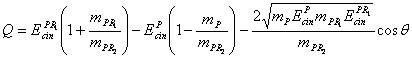(9)
Toate marimile sunt masurate in sistemul laboratorului (SL). Caldura (energia) de reactie este independenta de sistemul de referinta fiind definita in functie de masele de repaus.
Pentru reactii nucleare
endotermice 
. Energia cinetica minima necesara pentru
producerea unei reactii endoenergetice se numeste energie de prag. Ea
este suficienta pentru initierea procesului de interactie, astfel incat cei doi
produsi de reactie au viteza reciproca nula in sistemul centrului de
masa (SCM). De aceea, in SCM energia cinetica neta este nula.
Energiile cinetice ale produsilor de reactie in SL sunt nenule pentru ca viteza
centrului de masa este nenula in SL.
Energia cinetica totala este 
in SL, iar in SCM se poate scrie astfel:
(10)
Energia cinetica neta finala in SCM se obtine prin adaugarea caldurii (energiei) de reactie Q cu luarea in considerare a conditiei de producere la energia de prag. Se obtine:
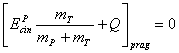(11)
de unde
(12)
cu Q < 0. La prag produsii de
reactie sunt emisi la 
.
Remarca. Formula obtinuta este aproximativa deoarece la estimarea energiei cinetice in SCM (ecuatia (10)) nu s-au luat in considerare efectele caldurii (energiei) de reactie determinate de rapoartele tuturor maselor. Formula completa se scrie astfel:
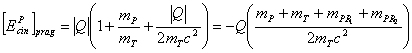(13)
Relatia (13) se reduce la relatia (12)
atunci cand 
.
I.5.11. Ciocnirea se poate scrie sub forma urmatoare:
Pentru simplificarea calculelor, se
poate face ipoteza ca: 
,
unde 
este masa nucleului tinta, T, iar 
este masa neutronului.
Calcularea impulsului in sistemul centrului de masa impune folosirea conditiei:
Luand in considerare viteza centrului de
masa, 
,
se poate scrie, in ipoteza ca nucleul tinta este in repaus:
Impulsul centrului de masa se poate scrie astfel:
Fie 
unghiul
de imprastiere al neutronului in sistemul centrului de masa si fie 
unghiul de imprastiere al aceluiasi neutron,
de impuls 
,
in sistemul laboratorului.
Se pot scrie relatiile de mai jos:
Energia cinetica a neutronului imprastiat se poate scrie astfel:
Luand in considerare ipotezele din enunt - medierea pe un numar mare de ciocniri si emisia izotropa a neutronilor imprastiati - relatia de mai sus, pentru energia cinetica medie a neutronilor imprastiati se poate scrie expresia de urmatoare:
deoarece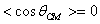 
,
in conditiile date.
Folosind expresiile vitezei si impulsului centrului de masa deduse anterior, expresia energiei cinetice medie a neutronilor imprastiati se poate scrie astfel:
unde 
.
Energia cinetica medie pierduta se poate scrie astfel:
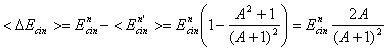
Fractia de energie cinetica medie pierduta este data de relatia:
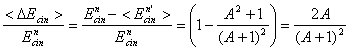(q.e.d.)
I.5.12. Reactia se poate scrie astfel:
Pentru calcularea fractiunii din energia cinetica pierduta de neutron se folosesc legile de conservare ale impulsului si energiei totale. Deoarece este o ciocnire elastica, centrala, se poate folosi si legea conservarii energiei cinetice. Se pot scrie relatiile de mai jos:
(1)
(2)
Deoarece
nucleul tinta este in repaus (
)
relatiile de mai sus se pot simplifica si se pot rescrie astfel:
(3)
(4)
Ecuatia (4) se poate scrie in termenii energiei cinetice astfel:
(5)
sau in forma de mai jos:
(6)
Pentru a
determina fractiunea de energie cinetica pierduta de neutron se ia in
considerare raportul 
. Luand in considerare relatia dintre
impulsuri, anume: 
,
se obtine:
(7)
Deoarece enuntul problemei nu da valori pentru impulsul sau energia cinetica a neutronului incident este de preferat sa se treaca in ecuatiile anterioare la folosirea energiilor cinetice. Se obtine:
(8)
Din relatiile (7) si (8) se obtine:
(9)
Efectuand calculele se obtine:
|
