In ultima perioada s-a acordat o atentie tot mai mare pentru modelarea si simularea bateriei in scopul exploatarii corecte si dezvoltarilor ulterioare in special pentru construirea de vehicule electrice si vehicule hibride. O corecta intelegere a bateriei din punct de vedere al performantelor, sigurantei, longevitatii sunt critice pentru aplicatii. Folosirea metodelor traditionale de testare pentru evaluarea caracteristicilor bateriei si obtinerea de performante superioare in conditii de operare complexe presupune timp si in cele mai multe cazuri este aproape imposibil. Pentru a prezice performantele baterie s-a incercat modelarea matematica. Nici unul dintre aceste modele nu are o acuratete completa si nici nu ia in considerare toti factorii de care depind performantele bateriei. Factorii care afecteaza comportamentul bateriei sunt:
Starea de incarcare - State of charge (SOC)
Capacitatea de stocare a baterie
Rata de incarcare/ descarcare
Temperatura
Varsta - durata de viata
Obiectivele acestor modelari este realizarea unor modele de baterie cu caracteristici cat mai apropiate de comportamentul unei bateri reale si adaugarea la standardele curente a informatiilor care permit extinderea cerintelor si necesitatilor automobilelor moderne. Ce se urmareste in principal este un model care sa permita o mai buna intelegere a comportamentului dinamic al bateriei in aplicatii.
Rezistenta interna (IR) masurata in miliohmi, este rezistenta totala in curent continuu a bateriei care este incarcata si in stare de functionare. Acest test este facut la 25 grade Celsius si consta in descarcarea bateriei timp de 1 minut la valoarea curentului de descarcare dupa 3 secunde de la inceperea procesului de descarcare si masurarea tensiunii dupa 3 secunde. A doua masuratoare se face dupa un timp de 3 minute masurand valoarea tensiunii. Rezistenta se calculeaza ca fiind dV/dI ( Volti /amperi ) [1],[2].
Rezistenta interna a acidului si a electrozilor: marime care ar trebui furnizata de producator. Este obtinuta prin masuratori experimentale la 25 grade Celsius si reprezinta rezistenta ionilor (elementul acid) si rezistenta electrozilor bateriei. Aceasta marime se foloseste in scopul de a separa fiecare componenta ce alcatuieste rezistenta interna a bateriei si deci pentru a nu se neglija astfel comportarea in functie de temperatura.
Capacitatea bateriei: Capacitatea bateriei este calculata folosind relatia lui Peukert C= In*t unde C si n sunt contante pentru fiecare model de baterie.
Tensiunea de incarcare si OCV / RSOC (Tensiunea in circuit deschis / Starea de incarcare relativa): pentru proiectare o problema dificila consta in determinarea starii de incarcare relativa (RSOC). Pentru aceasta sunt necesare doua caracteristici:
Tensiunea la borne in circuit deschis OCV (static)
Caracteristica OCV / RSOC
Modelul Shepherd este poate cel mai cunoscut si probabil cel mai adesea folosit in modelarile bateriei si in modelarile vehiculelor electrice hibride. Acest model descrie procesele electrochimice in termeni de tensiune si curent. Este folosit in stransa legatura ecuatia lui Peukert pentru a obtine tensiunea bateriei si starea de incarcare. [2]
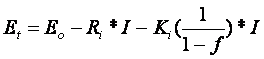
Unde
Et = tensiunea la bornele bateriei [volti]
Eo = tensiunea in circuit deschis la bornele bateriei cand bateria este complet incarcata [volti]
Ri = rezistenta interna a bateriei [ohmi]
Ki = rezistenta de polarizare [ohmi]
Q = capacitatea bateriei [amperi-ora]
I = curent instantaneu [amperi]
f = reprezinta fractiunea extrasa din baterie (capacitatea extrasa din baterie raportata la capacitatea Q0 a bateriei incarcate complet).
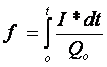
Daca bateria este incarcata complet atunci f ar tinde la zero si avem rezistenta de polarizare mare. Daca bateria este descarcata atunci f creste si atunci termenul din ecuatie care modeleaza rezistenta de polarizare scade.
Shepherd s-a bazat in cercetarile efectuate pe curenti de descarcare constanti dar de valori mici. Ecuatia lui a cauta sa gaseasca punctul minim de descarcare (de la care valoarea tensiunii la borne scade foarte rapid). Unnewehr si Nasar propun modificarea ecuatiei anterioare.
![]()
In cazul bateriei in circuit deschis sau fara sarcina tensiunea la borne se scrie mai simplu:
![]()
Unnewehr [3] si Nasar au definit rezistenta interna echivalenta:
![]()
Unde:
Ro = rezistenta interna a bateriei complet incarcata
KR = constanta experimentala
Aceasta
ecuatie incearca o modelare a rezistentei interne Ri in functie
de starea de incarcare SOC.
Combinand aceasta ecuatie cu cea a puterilor P=Et*Idesc, se poate
crea o noua relatie pentru calcularea curentului de descarcare:
![]()
Ecuatia de gradul doi are urmatoarea forma:
![]()
Din cele doua solutii dar va fi aleasa doar solutia de valoare mai mica:
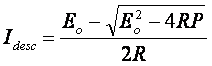

Figura 1.4 Modelul circuitului echivalent al bateriei pentru descarcare
In cazul in care bateria se incarca circuitul echivalent este dat in figura de mai jos:
Ecuatia circuitului este in acest caz de forma urmatoare:
![]()
inmultind ambii termeni cu I si combinand ecuatia puterilor se obtine:
![]()
Ecuatia de gradul doi are urmatoarea forma:
![]()
Pentru curentul de incarcare se obtine urmatoarea solutie:
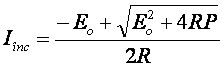

Figura 1.5. Modelul circuitului echivalent al bateriei pentru incarcare
Se poate demonstra ca puterea maxima pe rezistenta de sarcina se obtine pentru circuitul echivalent al bateriei atunci cand valoarea rezistentei de sarcina este egala cu valoarea rezistentei interne. Pornim de la relatia (1.11) si inlocuim in aceasta valoarea curentului I.
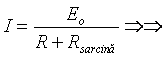
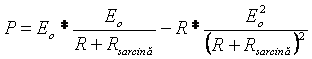
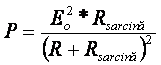
Se pune conditia ca derivata sa fie nula pentru putere maxima si se obtine:
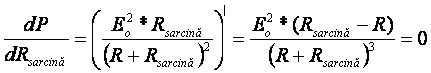
Pentru ca derivata sa fie nula trebuie indeplinita conditia
![]()
![]()
Valoarea maxima a puterii se obtine inlocuind in relatia (1.18) valoarea rezistentei de sarcina:
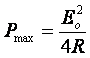
Acest model descris in [4],[5] consta intr-o sursa de tensiune in serie cu o rezistenta (asimilata ca rezistenta interna) si totul in paralel cu o combinatie serie rezistenta - condensator (modelul pentru supratensiune). Acest model nu este foarte corect deoarece elementele ce il compun iau alte valori in procesul de incarcare sau descarcare si depind direct de starea bateriei.
Acest model este o modificare neliniara a modelului anterior [6]. Circuitul echivalent are 5 sectiuni:
Supratensiunea este modelata de un circuit format dintr-un condensator si o rezistenta in paralel, iar acest circuit este inseriat cu Cb si Rp. Rezistenta in aceasta retea, R1, este modelata ca o rezistenta ce poate lua doua valori in functie de modul de lucru al baterie
Rezistenta interna este modelata de R1 si cele 2 diode in paralel si o rezistenta suplimentara Rs, care este in serie cu grupurile R1-C1 si Rp- Cb. Rezistenta interna este considerata deci a fi suma dintre R1 si Rs. Rs reprezinta electrolitul, placile, si rezistenta fluidului in vreme R1 reprezinta rezistenta datorata difuziei electrolitului. Ca si R1, Rs este modelata ca fiind formata din doua diode in paralel cu doua rezistente pentru a modela variatiilor datorate incarcarii si descarcarii.
Modelul este neliniar in sensul ca elementele Cb, Rs, Rp si R1 nu sunt constante dar ar trebui modelate in functie de tensiunea bateriei. Alt factor care ar trebui specificat este acela ca Rp are o dependenta de temperatura. Doar C1 este constant.

Figura 1.6. Modelul neliniar al bateriei - circuitul echivalent
Pentru a determina dependenta
de temperatura a rezistentei si a condensatorului s-au facut teste
experimentale iar rezultatele a fost introdus in formule de forma urmatoare :
![]()
Unde
K = constanta (factor de multiplicare)
W = factor de material
Vm= nivelul tensiunii la borne
Voc = tensiunea in circuit deschis
F = flatness factor
Si
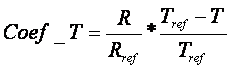
relatia pentru coeficientul de variatie cu temperatura al rezistentei Rp , unde
Acest model a fost verificat experimental si se
apropie de modelul real pentru bateriile cu plumb si cele cu Nickel - Cadmiu.
Acest model fundamentat in [7] este bazat pe modelul static care descrie tensiunea la borne ca functie de curentul de incarcare/descarcare. In acest model se mai iau in considerare si efectul polarizarii. Cele 3 ecuatii care descriu acest model sunt:
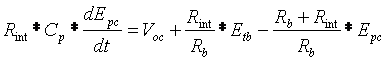
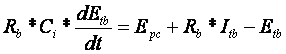

Unde:
Rint = rezistenta interna a bateriei [ohmi]
Cp = capacitate de polarizare
Epc = tensiunea pe condensatorul de polarizare
Voc = tensiunea in circuit deschis [volti]
Rb = rezistenta terminalului [ohmi]
Etb = tensiunea la bornele bateriei
Ci = capacitate incipienta a terminalului
Itb = curent de descarcare al bateriei [amperi
K = constanta de baterie
SOC = starea de incarcare
Pentru bateriile cu plumb Powell si colaboratorii in [8] au obtinut o relatie empirica pentru ultima ecuatie:
![]()
Starea de incarcare influenteaza cel mai mult performantele bateriei. Tensiunea in circuit deschis Voc in general descreste neliniar odata cu scaderea SOC Rezistenta interna Ri descreste usor pe masura cresterii SOC la nivele mici (< 0.3 din valoarea maxima a lui SOC), si apoi ramane constanta pana la valori de 0.6 din SOC. De la acest punct va creste foarte rapid.
Relatia dintre Ri si SOC a fost observata si descrisa de Ekdunke in [12].
Facinelli a folosit o relatie liniara intre Voc si Ri El a folosit curbe diferite pentru incarcare si descarcare [13].
|