Formalismul Hamilton

II.4.1.Variabile canonice. Spatiul fazelor

Se defineste impulsul generalizat canonic conjugat cu coordonata generalizata prin relatia:

Cele impulsuri generalizate împreuna cu cele coordonate generalizate formeaza un ansamblu de parametri, numiti variabile canonice.

Ansamblul celor variabile canonice defineste un spatiu cu dimensiuni, numit spatiul fazelor.

Un punct în spatiul fazelor reprezinta starea dinamica a sistemului mecanic ("pozitia" punctului în spatiul fazelor duce la cunoasterea impulsurilor si a coordonatelor generalizate, din care se pot gasi coordonatele si vitezele carteziene ale particulelor constituente ale sistemului).

Evolutia în timp a sistemului, data de:

este reprezentata în spatiul fazelor prin traiectoria punctului reprezentativ iar relatiile (II. 828f53i 37) constituie ecuatiile parametrice (parametrul este ) ale traiectoriei.

II.4.2.Ecuatiile canonice sau ecuatiile de miscare ale lui Hamilton

Pentru descrierea evolutiei unui sistem mecanic, în afara de functia Lagrange se mai poate utiliza functia Hamilton sau hamiltoniana sistemului, introdusa prin relatia:

Se observa ca aceasta functie are, ca si , dimensiunile unei energii.

Cu ajutorul functiei Hamilton se poate gasi o alta forma a ecuatiilor de miscare a unui sistem fizic, fie exprimând din (II. 828f53i 38) functia Lagrange, recalculând integrala de actiune si punând conditia ca ea sa fie un extremum pe traiectoria reala fie folosind ecuatiile Lagrange.

Vom recurge la a doua varianta:

- calculam diferentiala functiei :

-pe de alta parte, din (II. 828f53i 38) aceasta diferentiala se scrie:

Dar , deci al doilea si penultimul termen din expresie se reduc, astfel ca:

Din ecuatiile Lagrange:

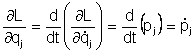
deci (II. 828f53i 40) devine:

- expresiile (II. 828f53i 39) si (II. 828f53i 41) coincid daca:

si

Relatiile (II. 828f53i 42) (a) si (b) formeaza un sistem de ecuatii diferentiale de ordinul întâi si constituie sistemul ecuatiilor canonice de miscare sau ecuatiile de miscare Hamilton.

Necunoscutele acestui sistem sunt si . Prin integrarea ecuatiilor (II. 828f53i 42) se obtin si constante de integrare care se pot determina daca se cunosc conditiile initiale ale problemei (la un moment dat ), adica:

II.4.3.Semnificatia fizica a functiei Hamilton

Presupunem un sistem conservativ de forte care actioneaza asupra unui sistem de puncte materiale cu grade de libertate. Fortele provin din potentialul deci:

iar

.

Atunci functia Hamilton se poate scrie:

Energia cinetica este o functie patratica omogena de vitezele generalizate, cu gradul de omogeneitate .

Observatii matematice: O functie este omogena de gradul în variabilele daca se poate scrie:

unde este o constanta.

Pentru o functie omogena de gradul în variabilele se poate scrie teorema lui Euler:

Pentru o functie omogena de gradul în toate variabilele sale, teorema lui Euler devine:

În cazul nostru, aplicând teorema lui Euler functiei cu , obtinem:

iar (II. 828f53i 46) devine:

deci functia Hamilton este tocmai energia totala a sistemului.

II.4.4.Coordonate ciclice

Consideram ecuatiile Lagrange sub forma:

Daca functia Lagrange nu contine explicit o coordonata , atunci:

Coordonatele generalizate care nu intra explicit în expresia functiei Lagrange se numesc coordonate ciclice iar impulsul canonic conjugat unei coordonate ciclice se conserva.

II.4.5.Parantezele Poisson

Fie doua functii de coordonatele canonice si de timp, si .

Prin definitie, paranteza Poisson a celor doua functii este:

Parantezele Poisson au urmatoarele proprietati:

1) Daca (constanta) sau (constanta):

sau

2) Sunt anticomutative, adica:

3)

4) (distributivitatea fata de adunare-scadere)

5)

6) a) Daca :

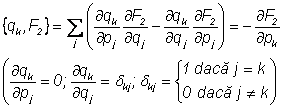
b) Daca :

În particular

7)

Cu ajutorul parantezelor Poisson se poate da o expresie concisa derivatei totale în raport cu timpul a unei functii de coordonatele canonice si de timp :

Dar si pot fi exprimate din ecuatiile Hamilton (II. 828f53i 42) deci:

Din aceasta relatie se observa ca daca o marime fizica exprimabila în functie de coordonatele canonice nu depinde explicit de timp si paranteza ei Poisson cu functia Hamilton este nula, atunci , deci marimea se conserva.

Cu ajutorul parantezelor Poisson si a proprietatilor 6) a) si b) se pot exprima sub o alta forma ecuatiile Hamilton.

Într-adevar, folosind proprietatea 6) a) pentru functia Hamilton:

iar din proprietatea 6) b) :

Introducând relatiile (II. 828f53i 52) si (II. 828f53i 53) în ecuatiile Hamilton (II. 828f53i 42), acestea devin:

Mentionam ca oricare ar fi formalismul folosit pentru rezolvarea unei probleme de mecanica (Lagrange, Hamilton sau Newton), rezultatele sunt aceleasi.

Practic, metoda de rezolvare a unei probleme cu ajutorul formalismelor mecanicii analitice consta în urmatoarele:

1. Se stabileste numarul gradelor de libertate ale sistemului (N - numarul punctelor materiale; l - numarul de legaturi);

2. Se aleg cât mai convenabil coordonatele generalizate si se exprima dependenta coordonatelor carteziene de coordonatele generalizate;

3. Se exprima componentele carteziene ale vitezelor în functie de coordonatele si de vitezele generalizate;

4. Se construiesc functiile ;

5. Se exprima cele impulsuri generalizate si se construieste functia Hamilton;

6. Se exprima cele conditii initiale pentru coordonatele generalizate si vitezele (sau impulsurile) generalizate, pornind de la conditiile initiale exprimate în coordonate carteziene;

7. Se scriu ecuatiile Lagrange (sau Hamilton) si se integreaza, determinând constantele de integrare din conditiile initiale si se gasesc coordonatele generalizate si impulsurile generalizate în functie de timp;

8. Se determina apoi dependenta de timp a coordonatelor si vitezelor carteziene.