Formalismul Lagrange

II.3.1.Ecuatiile lui Lagrange

Sa aratam ca principiul lui Hamilton (II.14) este echivalent cu un sistem de ecuatii diferentiale de ordinul al doilea. Vom calcula variatia a integralei de actiune atunci când coordonatele si vitezele generalizate sufera variatiile si de la traiectoria reala la una virtuala, infinit învecinata, la momentul .

Dar

(operatorii si sunt comutativi) astfel ca (II.15) 414h73e devine:

Consideram integrala a II-a si o rezolvam prin parti:

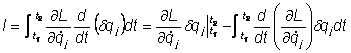
Ţinând seama de relatiile (II.13) primul termen este nul deci (II.17) devine:

Variatiile sunt arbitrare si independente deci integrala se va anula daca toti integranzii sunt nuli:

Acesta este sistemul ecuatiilor Lagrange. El este un sistem de ecuatii diferentiale de ordinul al doilea cu necunoscutele .

Rezolvarea sistemului conduce la aparitia a constante de integrare care se pot determina din conditiile initiale ale problemei - adica din cunoasterea coordonatelor generalizate si a vitezelor generalizate la un moment dat:

II.3.2.Proprietati ale functiei Lagrange

a) Functia Lagrange este aditiva: daca un sistem mecanic este compus din mai multe subsisteme care nu interactioneaza între ele, fiecare caracterizat de functia Lagrange , atunci functia Lagrange a întregului sistem va fi suma:

Aceasta relatie exprima faptul ca ecuatiile de miscare ale unui subsistem nu contin parametri ce caracterizeaza miscarea unui alt subsistem;

b) Multiplicând functia Lagrange cu o constanta, ecuatiile de miscare (II.19) nu se vor modifica. Acest fapt nu indica o nedeterminare a functiei Lagrange ci reflecta posibilitatea alegerii în mod arbitrar a sistemului de unitati de masura;

c) Functia Lagrange este determinata pâna la derivata totala în raport cu timpul a unei functii arbitrare de coordonate si timp.

Într-adevar, fie doua sisteme caracterizate de functiile Lagrange si cu proprietatea:

unde este o functie arbitrara de coordonatele generalizate si de timp.

Atunci integrala de actiune va fi:

iar

deci ecuatiile de miscare vor fi identice;

d) Pentru un sistem închis nu depinde explicit de timp - proprietate care decurge din uniformitatea timpului.

II.3.3.Expresii ale functiei Lagrange

Consideram un sistem de puncte materiale sub actiunea unui sistem de forte cu rezultanta . Daca sistemul nu este afectat de legaturi vor exista coordonate independente (proiectiile vectorilor de pozitie pe axele carteziene), , iar legea a II-a a dinamicii se scrie:

Energia cinetica a sistemului:

cu proprietatea , deci (II.23) devine:

Daca fortele sunt conservative ele provin dintr-un potential :

Comparând (II.24) cu (II.25) rezulta:

Trecând de la coordonatele la coordonatele generalizate (când exista legaturi) prin relatiile:

calculam:

Se observa ca:

astfel ca:

Al doilea termen din paranteza se scrie:

iar (II.28) devine:

Definind fortele generalizate prin relatia:

relatia (II.29) se scrie:

Pentru un sistem conservativ de forte, din (II.30) se obtine:

[în se poate trece la coordonatele generalizate prin relatiile (II.27)], astfel ca relatiile (II.31) se scriu:

Comparata cu relatia (II.26) în coordonate carteziene se observa ca la trecerea de la coordonatele carteziene la cele generalizate apare termenul suplimentar , care nu are echivalent în spatiul euclidian (energia cinetica depinde doar de viteze). Termenii de tipul sunt legati de curbura suprafetelor în spatiul de configuratie.

Comparând acum relatiile (II.32) cu ecuatiile Lagrange (II.19), (cu observatia ca functia depinde numai de coordonatele generalizate, nu si de vitezele generalizate), vedem ca ar fi identice daca:

Aceasta este expresia functiei Lagrange pentru un sistem de puncte materiale cu grade de libertate, sub actiunea unui sistem de forte conservative.

Pentru un sistem de puncte materiale în interactie:

care, prin schimbarile de variabile (II.27) si devine:

Pentru un sistem neînchis care interactioneaza cu un sistem aflat în miscare, se poate considera ca se misca într-un câmp exterior creat de sistemul . Acum va constitui un sistem închis, deci:

astfel ca pentru sistemul :

deci sistemul neînchis este descris de o functie Lagrange de tip obisnuit, cu diferenta ca energia potentiala poate sa depinda explicit de timp.