GHIDURI DE UNDA UNIFORME

Definitie : Ghidul de unda reprezinta un domeniu amplasat in jurul unei axe si delimitat de suprafete de discontinuitate a parametrilor electrici si magnetici ce asigura propagarea ghidata a campului electromagnetic pe directia axei sale. Ghidurile de unda se pot clasifica in functie de: mediu constructiv: ghiduri in care parametri electrici si mag 242j91c netici sunt constanti (ghiduri liniare ,omogene si izotrope), ghiduri in care parametri depind de intensitatea campului electromagnetic

(ghiduri neliniare), ghiduri in care

parametri electrici si magnetici depind de

coordonate (x,y,z-ghiduri neomogene), ghiduri in care parametri electrici si mag 242j91c netici au caracter tensorial (ghiduri anizotrope). Geometria ghidului: ghiduri uniforme ce au sectiunile transversale identice in orice punct pe axa longitudinala (ghiduri dreptunghiulare, circulare, eliptice,in H, in U, coaxial), ghiduri neuniforme la care sectiunile transversale nu sunt identice fie d.p.d.v. electric fie geometric (ghiduri piramidale,conice, exponentiale, axial neomogene)..Valoarea relativa a parametrior electrici: ghiduri metalice, dielectrice. Repartitia campului electromagnetic: ghiduri inchise, deschise. Distributia transversala a campului electric: ghiduri cu unda de suprafata.

Ecuatia undelor si ecuatia membranei.

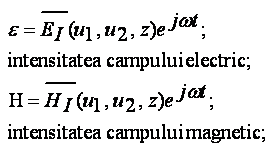
Ecutiile lui MAXWELL:

Ecuatiile de stare:

Pentru medii liniare , omogene si izotrope ecuatiile lui MAXWELL devin:

In regiunile cu densitate electrica nula : si deci pentru conditiile enuntate (medii liniare , omogene si izotrope) Deci :

In cazul ghidului uniform distributia transversala a campului electromagnetic nu depinde de punctul de pe axa de propagare:

In coordonate carteziene relatiile (*) devin pentru distributiile:

-transversale:

-longitudinale: in care:

Ecuatia undelor pentru componenta longitudinala devine:

-in coordonate curbilinii cilindrice:

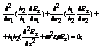
h1,h2,h3-coeficientii LAME.

-in coordonate curbilinii ortogonale:

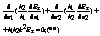
Relatiile (**) sunt cunoscute sub denumirea de ecuatiile membranei E.

Plecand de la ecuatiile (*) si (**) se pot definii modurile de propagare:

-modul de propagare TM (transversal magnetic) pentru care H_z=0 si E_z diferot de 0:

-modul de propagare TE (transversal electric) pentru care E_z=0 si H_z diferit de 0:

-modul de propagare TEM (transversal

electromagnetic) pentru care E_z=0 si H_z=0:

componentele transversale E_T si H_T sunt perpendiculare intre ele si sunt in faza:

Impedanta de unda:

Raportul intre componentele E₁ ,E₂ si H₁, H₂ ale campului transversal se numeste impedanta de unda. Astfel pe modul TM si

TEM H_z=0:

Pe modul TE si TEM E_z=0:

Impedanta de unda a spatiului liber:

Frecventa critica.

Constanta de propagare este legata de k prin relatia:

In cazul ghidului uniform , cu peretii perfect conductori si cu mediul interior dielectric perfect obtinem: Daca diferenta este pozitiva campul electromagnetic nu se propaga deoarece si deci componentele H_I si E_I vor avea forma de oscilatie, nu de unda. Daca diferenta este nula vom avea:

Frecventa corespunzatoare situatiei gama=0 se numeste frecventa critica:

Deoarece modul TEM are k=0 rezulta frecventa critica a modului TEM este 0. Modul fundamental se defineste drept modul de propagare cu frecventa critica minima. Deoarece modul TEM are f_c=0 modul TEM este modul fundamental.

Daca diferenta este negativa si campul electromagnetic se propaga deoarece si componentele sunt unde.

Densitatea de putere este definita prin expresia:

Puterea transmisa printr-o suprafata S este:

n-normala la suprafata S si da-elementul de arie.

Faza undei , functie de timp si de punct este:

Viteza de faza :

Viteza de grup: ii este

asociata propagarea energiei. De aceea cand se vorbeste despre viteza undei, se intelege viteza de grup.

Conditii la limita.

Conditiile la limita , la suprafata de separatie a doua medii (respectiv in ghidul uniform pe conturul sectiunii transversale exprima continuitatea componentelor tangentiale ale campului electric si ale componentelor normale ale campului inductie magnetica), adica:

De asemenea marimile H si D trebuie sa

indeplineasca conditiile:

in care J_s= densitatea de curent la limita [A/m] si q_s=densitatea superficiala de sarcina [C/m²]. Daca J_s=0 si q_s=0 rezulta:

Pentru doua medii liniare si izotrope

conditiile vor fi:

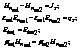
GHIDURI UNIFORME CU MOD DE PROPAGARE TEM.

Principalele ghiduri cu mod de propagare TEM sunt: placile metalice paralele, linia bifilara, cablul coaxial. Placile metalice permit propagarea undei plane uniforme ce se caracterizeaza prin faptul ca are componentele independente de pozitia in planul transversal. Linia bifilara si cablul coaxial permit propagarea undei plane neuniforme. In afara modului TEM (modul fundamental), aceste ghiduri pot admite si moduri superioare (adica TE si TM). Structurile ghidante cu mod fundamental TEM sunt denumite linii de transmisie. Structurile ghidante cu mod TE sdi TM sunt denumite ghiduri de unda. Pentru liniile de transmisie (mod TEM) notiunea de tensiune este valabila deoarece campul electric transversal E_T deriva dintr-un potential.

ECUATIILE LINIILOR

Tensiunea in plan transversal este:

A si B sunt puncte din planul transversal intre care ne intereseaza diferenta de potential.

Deoarece k=0 pentru modul TEM ecuatia undelor (sau ecuatia membranei) in coordonate carteziene este:

iar duala acesteia

Propagarea undei de-a lungul liniei este data de legea : Inlocuind si integrand intre doua puncte A si B din planul transversal obtinem:

-ecuatia liniilor pentru tensiune.

Folosind ecuatiile lui MAXWELL si tinand cont de conditiile la limita obtinem ecuatia curentului ce circula prin linia de transmisie:

Exprimarea ecuatiilor liniilor cu ajutorul parametrilor lineici.

Determinarea functiilor U(z) si I(z) se poate face analizandu-se modelul cu parametrii distribuiti ai liniei . In acest sens se definesc parametrii lineici:

[W/m]-rezistivitatea lineica;

[F/m]-capacitatea lineica;

[H/m]-inductanta lineica;

[S/m]-conductanta de pierderi lineica a izolatiei;

-reprezinta o unda cu amplitudinea ce se propaga in sensul pozitiv al axei, numindu-se de aceea unda directa.

-unda ce se propaga in sensul negativ ala axei cu amplitudinea numindu-se unda inversa.

Viteza de faza pentru aceste unde este

Lungimea de unda este :

Linia terminata pe o sarcina oarecare.

Solutiile generale ale tensiunii si curentului contin doua constante arbitrare si care depind de conditiile la limita ale problemei. Consideram ca linia este terminata la o extremitate pe o impedanta Z_s. Fata de sarcina unda directa reprezinta o unda incidenta, iar cea inversa trebuie interpretata ca unda reflectata.

Definim coeficientul de reflexie al tensiunii la sarcina:

Daca Z_S=Z_C rezulta G=0, iar pe linie nu exista decat unda directa. Sarcina care satisface aceasta cerinta se numeste sarcina adaptata, iar linia terminata astfel se numeste linie terminata adaptat.

Linia fara pierderi.

Linia fara pierderi este un model teoretic de linie idealizat, alcatuit din conductoare perfecte separate prin dielectrici perfecti. Particularizand relatiile prezentate anterior obtinem:

-constanta de propagare:

-viteza de faza:

-viteza de grup:

Se observa ca viteza de faza si viteza de grup nu depind de frecventa ceea ce inseamna ca linia fara pierderi este nedispersiva.

-ecuatiilen tensiunii si curentului de linie:

-impedanta caracteristica:

independenta de frecventa.

-coeficientul de reflexie al tensiunii:

-coeficientul de reflexie al puterii:

OBS. Linile reale au pierderi , dar in multe cazuri aceste pierderi pot fi neglijate daca sunt satisfacute conditiile:

(F).

Linia cu pierderi mici.

Neglijarea totala a pierderilor chiar si in cazul indeplinirii conditiilor (F) conduc la rezultate eronate. De aceea, pentru cazul indeplinirii acestor conditii se poate folosi modelul liniilor cu pierderi mici.

-constanta de propagare:

-impedanta caracteristica:

-constanta de atenuare:

Linia fara distorsiuni

Daca parametri lineici satisfac conditia :

linia este fara distorsiuni, adica semnalele sunt transmise fara distorsiuni pentru ca :

-atenuarea nu depinde de frecventa;

-defazajul este proportional cu frecventa, adica viteza de grup este constanta.

Impedanta caracteristica in cazul satisfacerii conditiei (G) este:

Constanta de propagare devine:

La liniile reale pentru indeplinirea conditiei (G) la frecvente relativ joase este incarcata linia cu inductante concentrate.