INTRODUCERE IN TEHNICA MASURARII

INTRODUCERE IN TEHNICA MASURARII

CONCEPTUL DE MASURARE

Masurarea este un proces practic (empiric), un act de cunoastere cantitativa si calitativa a realitatii, a obiectelor si a mediului in care ne desfasuram activitatea. Ea se finalizeaza prin obtinerea directa sau prin calcul a valorilor marimilor care ne intereseaza.

O marime poate fi oricare proprietate comuna, oricare manifestare sau element de caracterizare al unei clase de obiecte, fenomene ori procese reale, care in diverse circumstante poate avea mai multe stari, valori sau nuante.

Reprezentarea in mintea umana a unei marimi, a valorii ei, se face printr-o abstractizare, printr 252e42c -un model sau imagine asociata marimii reale. Domeniul in care se incadreaza reprezentarea este in majoritatea cazurilor o submultime a numerelor reale iar reprezentarea unei stari concrete in aceasta submultime se face printr-un numar care se numeste masura sau valoarea marimii masurate.

De exemplu, gradul de incalzire al unui corp poate fi determinat dupa temperatura acestuia, care poate fi masurata si exprimata in ^oC, in ^oF sau in alte unitati de masura. Prin urmare valoarea temperaturii, data de un termometru, este masura temperaturii corpului.

O conditie esentiala a reprezentarii unei marimi in mintea umana o constituie univocitatea dintre valoarea efectiva, reala a marimii supuse masurarii si valoarea reprezentata ca efect al masurarii.

In general, in sfera realitatii un obiect, fenomen sau proces dat este caracterizat prin multimea M(M₁, M₂ ,, M_i,) a marimilor ce-l definesc si prin multimile de valori ale acestor marimi: X₁ (x₁₁, , x_1N), X₂ (x₂₁, , x_2P), , X_i (x_i1, , x_iR). In sfera abstractizarii obiectul, fenomenul sau procesul respectiv este perceput prin multimea M* a marimilor reprezentate si prin multimile de valori ale acestor marimi: Y₁ (y₁₁ ,, y_1S), Y₂ (y₂₁ ,, y_2T) ,, Yj (y_j1 ,, y_jv), asa cum se sugereaza in figura 1.1.

Marimile reale pot fi reprezentate prin relatiile:

(1.1)

astfel incat pentru elementele multimii Y sa existe reprezentarea inversa:

(1.2)

cu indeplinirea conditiei:

, (1.3)

pentru toate elementele multimii X.

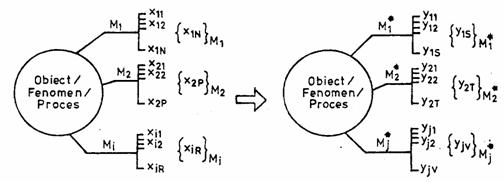
Fig.1.1. Modelul procesului de masurare.

In relatia (1.2) functia f^-1, notata cu j, semnifica reprezentarea inversa fata de functia f, ceea ce inseamna ca in cazul matematic ideal reprezentarea f este reciproc uniforma in domeniul multimii X. Nu este, insa, necesar ca numarul elementelor multimii X sa fie egal cu numarul elementelor multimii Y.

Din nefericire nu toate marimile naturale pot fi masurate, ci numai submultimea marimilor masurabile, cuprinsa in conjunctia marimilor observabile si a marimilor reperabile, asa cum se sugereaza in diagrama Venn din figura 1.2.

Marimile observabile sunt acele marimi asupra carora se pot gasi discriminari calitative si/sau cantitative: marimile reperabile sunt cele care sunt ordonabile si asupra carora se pot construi scari de masurare, iar marimile masurabile cele pentru care se pot construi si mijloace tehnice efective de masurare.

Rezulta deci ca masurarea este conditionata de:

observabilitatea marimii de masurat;

posibilitatea stabilirii a cel putin unei scari de masurare;

posibilitatea realizarii unor mijloace de masurare.

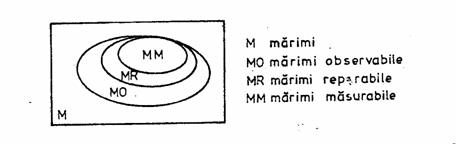
Fig.1.2. Submultimea marimilor masurabile.

Masurarea poate fi tratata si interpretata sub mai multe aspecte.

Sub aspect matematic, masurarea este privita ca un proces experimental de comparare a marimii ce se masoara, x, cu o alta marime de aceeasi natura cu ea, numita unitate de masura u_m, pentru a obtine un rezultat numeric sub forma:

. (1.4)

Rezultatul masurarii este un numar adimensional care arata de cate ori unitatea de masura este cuprinsa in marimea masurata. Acest rezultat exprima valoarea numerica a marimii masurate si este invers proportional cu unitatea de masura adoptata.

Daca o marime x se masoara cu doua unitati de masura diferite u_m1 si respectiv u_m2 pe baza ecuatiei masurarii avem:

. (1.5)

Din cele doua ecuatii se deduce ca:

(1.6)

Raportul k dintre u_m1 si u_m2 se numeste factor de transformare si reprezinta numarul cu care trebuie inmultita valoarea numerica a unei marimi, masurate cu o unitate de masura, pentru a obtine valoarea numerica a aceleiasi marimi, dar exprimata cu alta unitate de masura.

Sub aspect tehnic, masurarea este privita ca un proces de achizitie si de transformare succesiva a informatiei despre o anumita marime cu scopul compararii acesteia cu o scara conventionala sau cu o unitate de masura si folosirea rezultatului acestei operatii in diverse activitati. Intereseaza deci nu numai rezultatul obtinut, ci si forma in care el este furnizat, deoarece urmeaza a fi folosit fie de om, fie de diverse echipamente in productie, in proiectare, in cercetare s.a.

Sub aspect informational, masurarea este privita ca un proces experimental de inlaturare a unei nedeterminari asupra unei marimi de masurat x, prin determinarea (localizarea) unui interval cat mai ingust in care sa se afle marimea respectiva.

Sub aspect cibernetic, masurarea este privita ca un proces ce are loc intr-un sistem in care marimea de masurat x este supusa unor transformari succesive pentru a se obtine la iesirea acestuia o marime y, dependenta de x.

Pentru intelegerea corecta a conceptului de masurare este necesar sa facem unele sublinieri.

Se masoara proprietatile obiectelor si fenomenelor si nu obiectele si fenomenele in sine. Trebuie deci definit foarte clar conceptul de proprietate care se masoara, ca o notiune generala specifica unei categorii de obiecte sau fenomene. Prin urmare, sub acest aspect, proprietatea are un caracter abstract si numai formele ei particulare de manifestare, legate de existenta unui obiect sau fenomen real concret, pot fi masurate. De exemplu, nu se masoara lungimea, masa, temperatura, viteza ca atare ci numai lungimea, masa, viteza unui obiect concret. In fizica aceste proprietati poarta denumirea de marimi fizice, iar numerele atribuite lor ca rezultat al diverselor manifestari ale lor se numesc valori sau masuri.

Obiectelor si fenomenelor le sunt proprii un ansamblu de proprietati ale caror manifestari apar simultan. Prin procesul de masurare se poate determina numai una dintre ele, facand abstractie de existenta celorlalte, sau se pot masura proprietati globale, determinate de doua sau mai multe proprietati primare.

Necesitatea masurarilor a aparut din cele mai vechi timpuri, odata cu aparitia civilizatiei umane, fiind ceruta de necesitati de ordin practic.

Latura teoretica a tehnicii masurarilor a aparut si s-a dezvoltat la finele secolului trecut, iar elaborarea unei teorii moderne a masurarilor s-a realizat in ultimele patru decenii. Aceasta teorie ca si alte realizari ale stiintei contemporane a facut posibila aparitia unei stiinte a masurarii, denumita metrologie.

Metrologia este o ramura a stiintei care are ca obiectiv elaborarea si perfectionarea metodelor si mijloacelor de masurare a marimilor de interes general, elaborarea si/sau perfectionarea etaloanelor metrologice precum si elaborarea de norme privind conditiile pe care trebuie sa le indeplineasca mijloacele de masurare si utilizatorii acestora.

Principalii factori implicati intr-o masurare sunt:

marimea de masurat sau masurandul cu proprietatea sau manifestarea specifica ce o face masurabila;

scara/scarile de masurare si unitatea/unitatile de masura adoptate;

metoda care sta la baza procesului de masurare, care inglobeaza procedeul experimental prin care se realizeaza operatia de masurare, precum si mijloacele tehnice de realizare a acesteia;

prelucrarea rezultatelor primare, manual sau automat, cu scopul obtinerii unui rezultat final cat mai reprezentativ, cat mai exact si sub o forma adecvata pentru utilizator.

Din examinarea celor patru elemente constitutive ale operatiei de masurare rezulta ca metrologia este o stiinta cu un caracter interdisciplinar. In fundamentarea conceptelor privind evidentierea proprietatilor fizice ale marimilor de masurat privind metodele de masurare, scarile si unitatile de masura este implicata in primul rand fizica. In fundamentarea procedurilor de prelucrare a rezultatelor primare este implicata matematica, iar in realizarea mijloacelor fizice de masurare, a etaloanelor s.a. care in unele cazuri sunt instalatii de mare complexitate sunt implicate si alte stiinte tehnice: electronica, electrotehnica, mecanica, automatica, informatica s.a.

Implicatiile masurarilor in desfasurarea oricarei activitati au impus stabilirea unor reglementari juridice referitoare la operatiile de masurare. Ca urmare, in afara sferei obiectivelor ei stiintifice, metrologia mai cuprinde si un ansamblu de prevederi legale, acte normative si chiar institutii si organisme menite sa aplice in practica masuri organizatorice si tehnice pentru a asigura unificarea si corectitudinea masurarilor, adica ceea ce se numeste metrologie legala.