Legile electrolizei
Am
aratat ca prezenta unui curent electric intr-un conductor reprezinta un
transport de sarcini electrice. Densitatea fluxului de sarcini electrice este
caracterizata de densitatea de curent electric 
. Deoarece
purtatorii de sarcina electrica 
poseda si o masa 
, rezulta
clar ca transportul de sarcina electrica este insotit intotdeauna si de un
transport de masa. Densitatea fluxului de masa 
reprezinta masa de substanta ce trece in
unitatea de timp prin unitatea de arie a sectiunii transversale din conductorul
respectiv. Efectuand un rationament analog cu cel pentru calculul lui 
, se ajunge
simplu la expresia:
; (5.29)
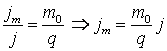. (5.30)
Formula (5.30) reprezinta legea lui Faraday a electrolizei sub
forma locala (sau diferentiala), care afirma ca densitatea fluxului de masa
este proportionala cu densitatea curentului electric. Coeficientul de
proportionalitate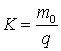 
se numeste echivalent electrochimic. La metale
purtatorii de sarcina sunt electronii caracterizati de masa si sarcina 
, astfel ca
pentru 
obtinem:
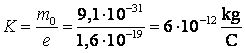
Se poate observa ca in cazul metalelor transportul de masa este neglijabil.
La
electroliza, unde curentul electric este caracterizat de deplasarea unor ioni
cu mase de mii de ori mai mari decat masa electronului, iar sarcina electrica este egala sau de cateva ori mai mare decat
sarcina electronului, transportul de masa devine sesizabil. Notand cu 
numarul de electroni pierduti sau capturati de catre atomul din care rezulta ionul
respectiv (valenta ionului), putem
scrie:
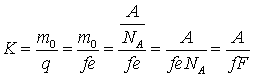
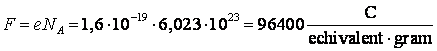
unde
este masa atomica a substantei respective si
se exprima in grame, 
este numarul lui Faraday, iar 
este echivalentul chimic al substantei depuse
la un electrod.
Inmultind
(5.30) cu 
rezulta:
, (5.31)
unde
, astfel ca
(5.31) se va scrie sub forma:
sau
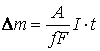. (5.32)
Formula
(5.32), reprezinta forma macroscopica a legii lui Faraday, indicand faptul ca
masa 
depusa pe unul din electrozi este
proportionala cu intensitatea curentului electric 
si cu timpul 
in care curentul respectiv trece prin
electrolit. Deoarece produsul 
reprezinta chiar sarcina electrica ce trece
prin solutie (printr-o sectiune transversala a electrolitului), formulele de
mai sus se mai pot scrie sub forma:
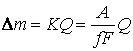. (5.33)
|
