MARIMI SI UNITATI DE MASURA - Relatii intre marimi

MaRIMI sI UNITatI DE masura

1. Marimi

Marimile de masurat sunt de o foarte mare diversitate si pot fi clasificate dupa numeroase criterii. Aceeasi situatie, ba chiar mai diversificata, o prezinta si unitatile de masura ale acestor marimi, deoarece pentru aceeasi marime pot exista mai multe unitati de masura.

Dupa caracterul dimensional deosebim:

marimi monodimensionale scalare;

marimi bi sau multidimensionale: vectori, tensori, rotori s.a.;

Dupa natura marimilor deosebim:

marimi electrice: tensiune, curent, putere, sarcina electrica, rezistenta, capacitate, inductanta s.a.;

marimi mecanice; lungime, masa, densitate, forta, presiune, vascozitate, viteza, acceleratie s.a.;

marimi hidrodinamice: debit, cadere de presiune s.a.

2. Relatii intre marimi

Legile fizicii, reprezentand relatii intre mai multe marimi, se exprima prin formule matematice sau prin formule fizice.

In exprimarea unei legi printr-o formula matematica operanzii reprezinta marimi, facand abstractie de unitatile de masura cu care acestia se masoara. In cazul aplicatiilor practice se folosesc formule fizice in care intervin valorile masurate ale operanzilor. Prin urmare, formulele fizice pot fi diferite intre ele si fata de formulele matematice intrucat trebuie sa se tina seama de unitatile de masura adoptate pentru marimile care intervin in ele.

Ceea ce face ca formulele sa se deosebeasca intre ele este aparitia in formula fizica a unui coeficient dependent de unitatile de masura in care se exprima marimile. Acest coeficient este denumit coeficient parazit. Sa luam ca exemplu formula matematica ce exprima legea fundamentala a dinamicii:

, (1.17)

unde F este forta care imprima masei M acceleratia A.

Pentru folosirea practica a acestei formule trebuie utilizate valori masurate pentru F, M si A alegand unitatile de masura u_f, u_m si u_a. Valorile masurate vor fi:

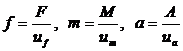. (1.18)

Formula fizica se obtine din formula matematica tinand seama de unitatile de masura:

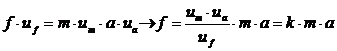(1.19)

unde este factorul care tine seama de unitatile de masura adoptate.

In exemplul dat, unitatile de masura pentru forta, masa si acceleratie au fost alese arbitrar. Exista posibilitatea ca acestea sa fie astfel alese incat coeficientul k sa fie egal cu 1. In acest caz insa unitatile de masura nu mai pot fi alese arbitrar. Din relatia

(1.20)

se deduce ca pentru a rezulta k = 1, odata alese doua dintre unitatile de masura, a treia unitate de masura rezulta din cele doua.

Prin adoptarea unui ansamblu de unitati de masura astfel incat k = 1 formula fizica se identifica cu formula matematica. Unitatile de masura astfel alese se numesc unitati coerente iar relatiile de forma 1.20 se numesc relatii de conditie deoarece indica modul in care anumite unitati de masura dintr-o formula le conditioneaza pe celelalte.

3. Sisteme de unitati de masura

In practica, pentru exprimarea marimilor fizice se folosesc formule fizice in care intra coeficientul k. Pentru a obtine formule fizice cat mai simple, cu k = 1, urmeaza sa se aleaga in mod corespunzator unitatile de masura. Aceasta insa este posibila prin limitarea numarului de unitati de masura alese arbitrar si prin adoptarea unor unitati de masura impuse de cele alese. Se ajunge astfel la o anumita subordonare si diferentiere a marimilor si unitatilor de masura dupa cum urmeaza.

Marimile pentru care unitatile de masura sunt alese arbitrar (conventional) se numesc marimi fundamentale si respectiv unitati de masura fundamentale, pe cand celelalte marimi pentru care unitatile de masura se aleg in functie de cele fundamentale se numesc marimi derivate si respectiv unitati de masura derivate.

Totalitatea unitatilor de masura fundamentale si derivate, care formeaza un ansamblu coerent pentru un anumit domeniu de masurare, constituie ceea ce se numeste un sistem de unitati de masura.

La alcatuirea unui sistem de unitati de masura trebuie, deci, sa se stabileasca numarul de marimi si unitati de masura fundamentale, numarul de marimi si unitati de masura derivate si sa se nominalizeze care dintre marimile sistemului sunt adoptate ca marimi fundamentale si care sunt adoptate ca marimi derivate.

Numarul marimilor si unitatilor de masura fundamentale poate fi stabilit pe baza urmatorului principiu: daca pentru descrierea fenomenelor fizice dintr-un anumit domeniu exista un numar R de legi (relatii) fizice independente, care leaga intre ele N marimi (N>R), atunci numarul minim de marimi si respectiv de unitati de masura fundamentale M este dat de relatia:

M = N - R . (1.21)

Nominalizarea acestor marimi si unitati de masura se face dupa criterii care tin cont de simplitatea si comoditatea operatiilor de masurare si definire, si anume:

marimile si unitatile fundamentale sa poata fi asociate unor fenomene reprezentative pentru domeniul respectiv si sa aiba proprietati invariante in timp si spatiu;

unitatile fundamentale sa poata fi realizate si reproduse in conditii avantajoase sub forma de etaloane;

intre unitatile fundamentale si cele derivate sa existe relatii simple pe baza carora sa poata fi definite si realizate usor unitatile derivate;

valorile efective ale unitatilor fundamentale se adopta tinand seama de considerente practice privind utilizarea lor si a unitatilor derivate, precum si de posibilitatile de realizare a unor multipli sau submultipli corespunzatori cerintelor practice.

Exista numeroase sisteme de unitati de masura care satisfac aceste cerinte pentru diverse domenii: MK_fS, CGS, MKS s.a. Existenta acestui mare numar de sisteme de unitati de masura, ca si a altor unitati de masura care nu fac parte dintr-un sistem a determinat o ampla activitate in vederea definirii si adoptarii unui sistem de unitati coerent, practic, simplu, cu aplicabilitate in toate domeniile stiintei si tehnicii. Ca urmare, la cea de a 11-a Conferinta Generala de Masuri si Greutati din 1960, a fost adoptat Sistemul International de unitati, SI, la care a aderat si tara noastra, unde este legiferat prin Legea metrologiei nr. 27/1978 si STAS 637-68.

4. Sistemul international (SI)

Intrucat tara noastra, ca si multe alte tari europene, a aderat la SI si in lume exista tendinta de generalizare a acestui sistem, vom prezenta succint elementele esentiale ale acestuia.

SI contine 7 unitati de masura fundamentale: metrul (m), kilogramul (kg), secunda (s), amperul (A), Kelvinul (K), molul (mol), candela (cd), doua unitati de masura suplimentare: radianul (rad) si steradianul (sr), precum si 34 unitati derivate, toate acestea fiind nominalizate si definite simbolic si dimensional in tabela 1.1.

Unitatile de masura fundamentale ale SI sunt definite astfel:

unitatea de lungime este metrul , (m), care este egala cu 1650763,73 lungimi de unda in vid ale radiatiei care corespunde tranzitiei intre nivelele 2p₁₀ si 5d₅ ale atomului de Kripton 86;

unitatea de masa este kilogramul, (kg), adica masa prototipului international din Pt - Ir, pastrat la Paris;

unitatea de timp este secunda, (s), care este durata a 9192631770 perioade ale radiatiei corespunzatoare tranzitiei intre cele doua nivele hiperfine ale starii fundamentale a atomului de Cesiu 113;

unitatea de intensitate a curentului, amperul (A), reprezinta intensitatea curentului care mentinut in doua conductoare paralele, rectilinii, de lungime infinita si sectiune circulara neglijabile, asezate in vid la distanta de 1 m unul de altul ar produce intre acestea pe lungime de 1 m o forta egala cu  2 10^-7 N;

unitatea de temperatura, Kelvin, (K), reprezinta fractiunea 1/273,16 din temperatura termodinamica a punctului triplu al apei;

unitatea pentru cantitatea de substanta, molul (mol), reprezinta cantitatea de substanta a unui sistem care contine atatea cantitati elementare cati atomi exista in 0,012 kg de carbon 12;

unitatea de intensitate luminoasa, candela, (cd), reprezinta intensitatea luminoasa in directia normalei, a unei suprafete de 1/600.000 m², a unui corp negru la temperatura de solidificare a Pt, la presiunea de 101.325 N/m²;

unitatea pentru unghiul plan, radianul, (rad), reprezinta unghiul plan cu varful in centrul unui cerc, care delimiteaza pe circumferinta un arc, a carui lungime este egala cu raza cercului;

unitatea pentru unghiul solid, steradianul, (sr), reprezinta unghiul solid cu varful in centrul unei sfere, care delimiteaza pe suprafata acesteia o arie egala cu aria unui patrat a carui latura este egala cu raza sferei.

Pentru a facilita scrierea valorilor numerice mari si foarte mari ca si a celor mici si foarte mici in SI se folosesc multiplii si respectiv submultiplii prezentati in tabela 1.2. 

Numarul unitatilor de masura cunoscute si folosite pana in prezent este de ordinul miilor, mai ales daca se ia in consideratie multiplii si submultiplii acestora. Unele dintre ele se folosesc cu precadere in anumite zone geografice iar altele - in alte zone. De exemplu, unitati de masura precum foot, inch, mille, yard, barel, pound, ounce se folosesc in tari de cultura anglo-saxona, in timp ce unitatile din SI, KGS, MKS s.a. se folosesc in tarile europene continentale.

in aceasta situatie de mare diversitate a unitatilor de masura este de foarte mare importanta sa se cunoasca si sa se opereze corect cu coeficientii de transformare a rezultatelor numerice obtinute cu unitati de masura diferite.

5. Echivalenta masurilor obtinute cu unitati de masura diferite

Pe baza ecuatiei masurarii cu scari de raport, conform careia o marime M este egala cu produsul dintre unitatea de masura U_m adoptata si valoarea numerica a marimii masurate se deduce ca daca pentru masurarea aceleiasi marimi se folosesc doua unitati de masura, U_m1 si U_m2 atunci raportul acestor unitati este:

(1.22)

Din aceasta relatie se vede ca valoarea numerica a unei marimi este invers proportionala cu unitatea de masura adoptata pentru masurare.

Raportul k dintre U_m1 si U_m2 se numeste factor de transformare si reprezinta numarul cu care trebuie inmultita valoarea numerica a unei marimi masurate cu o unitate de masura pentru a obtine echivalentul sau exprimat intr-o alta unitate de masura.

Tabelul 1.1. Unitati de masura ale Sistemului International

Tabelul 1.2.Multiplii si submultiplii unitatilor de masura.

Echivalenta masurilor monodimensionale. in cazul masurilor / marimilor monodimensionale, trecerea de la exprimarea intr-o anumita unitate de masura la exprimarea in alta unitate de masura este simpla si se reduce la multiplicarea rezultatului masurarii cu factorul de transformare.

Astfel, daca pentru lungime in loc de unitatea de masura din SI, care este metrul, se utilizeaza o alta unitate de masura, de exemplu inch, rezultatul masurarii in metri se obtine prin multiplicarea rezultatului in inch cu un coeficient  de transformare inch-metru. In cazul de fata 1 inch = 0,0254 m iar coeficientul de transformare este k = 0,0254. Daca o lungime l se masoara in inch, iar rezultatul masurarii este l=10,5 inch, echivalentul sau in metri este l_m=kl_i adica l_m=0,0254 x10,5=0,2667 m.

Daca se masoara arii sau volume folosind unitatea de lungime / latime / grosime inch si se doreste exprimarea rezultatului masurarii in unitatea de lungime / latime / grosime, in metri, coeficientul de transformare pentru arie trebuie luat la puterea a doua, iar cel pentru volum trebuie luat la puterea a treia.

Exemplu. O arie de 15 inch² are echivalentul 15x(0,0254)² in m², iar un volum de 20 inch³ are echivalentul 20x(0,0254)³ in m³.

Echivalenta masurilor multidimensionale In cazul marimilor derivate multidimensionale ca de pilda presiunea, debitul, puterea, coeficientul de transformare se determina din coeficientul de transformare al marimilor implicate in aceea marime derivata.

In cazul presiunii, definite ca raport dintre forta si suprafata, unitatile de masura fundamentale in SI sunt Newtonul [N] pentru forta si [m² ] pentru arie, pe cand in sistemul FPS unitatea de masura pentru forta este [lbf], iar pentru arie este [in²].

Avand in vedere ca 1 lbf = 4,448 N si 1 in = 0,0254 m ( 1 m² = 6,452 10^-4 m²) rezulta ca pentru transformarea masurii din lbf/in² in masura N/m² se utilizeaza coeficientul de transformare:

(1.23)

prin urmare rezultatul masurarii in N/m² se obtine din rezultatul masurarii in lbf/in², multiplicat cu coeficientul k=6,8948 x10³. In anexa 1.1. sunt prezentate cateva tabele cu factorii de transformare pentru cateva din cele mai uzuale marimi.