Miscarea browniana

In aceasta lucrare vom observa la microscop miscarea browniana a particulelor din fumul de tigara si vom verifica legea lui Einstein referitoare la miscarea browniana.

Materiale necesare

Microscop biologic trinocular cu sistem video de preluare a imaginilor, camera cu fum, si appletul:

In 1827, studiind reproducerea plantelor, in particular firisoarele de polen – cu dimensiuni de ordinul a 10^-6 m , marele botanist Robert Brown observa ca particulele foarte fine, aflate in suspensie intr-un fluid, au o miscare dezordonata, permanenta, dependenta de temperatura. Initial el a crezut ca acele particule sunt „vii”, dar, tot el a aratat ca acest lucru nu este adevarat, deoarece particule fine de materie anorganica, cuart provenit din monumentul Sfinxului, prezinta aceeasi miscare dezordonata, permanenta. Fenomenul a fost explicat, mai tarziu, prin miscarea termica a moleculelor lichidului. Daca particula in suspensie este suficient de mica, ciocnirile moleculelor nu se mai compenseaza si particula capata o miscare in directia rezultantei fortei datorate ciocnirilor cu moleculele. Daca particula este de dimensiuni mai mari, inertia crescuta a acesteia si dimensiunile sporite fac ca impulsurile moleculelor sa se compenseze reciproc si miscarea browniana inceteaza. Miscarea browniana confirma conceptia cinetico-moleculara despre natura fenomenelor termice.

In 1905 Einstein a publicat o teorie a miscarii browniene, aratand ca media patratului deplasarii particulelor browniene este proportionala cu timpul de miscare, in conditii izoterme: . Scopul acestei lucrari este sa verificam aceasta dependenta.

Ecuatia de miscare, proiectata pe o axa, a particulelor browniene este:

(1)

unde F₁ este forta rezultanta datorata ciocnirilor cu moleculele de lichid, iar F₂  este forta de rezistenta care se opune miscarii si care depinde de vascozitatea lichidului, de viteza particulei browniene si de raza particulei r. Este o forta de tip Stokes, adica:

(2)

unde r este raza particulei sferice,  este viscozitatea fluidului in care este imersata.

Ecuatia (1) devine:

(3)

In continuare vom integra aceasta ecuatie si vom face medierea temporala a termenilor care o compun. Vom inmulti ecuatia 3 cu x si obtinem:

(4)

Tinand cont ca:

si ca:

,

obtinem:

.   (5)

Mediem in raport cu timpul termenii acestei ecuatii, tinand cont de faptul ca masurarea lor dureaza un interval de timp indelungat in raport cu perioada ciocnirilor suferite din partea moleculelor. Datorita caracterului haotic al ciocnirilor moleculelor, termenul care contine pe x la putere impara (xF₁) se anuleaza. Cu notatia: , ecuatia (4) devine:

   (6)

Termenul reprezinta energia cinetica medie a particulei browniene si in acord cu teoria cinetico-moleculara, considerand doar proiectia miscarii pe axa Ox, avem:

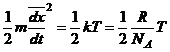   (7).

Inlocuind (7) in (6) obtinem:

             (8)

Prin separarea variabilelor obtinem expresia:

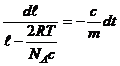
pe care apoi o integram:

    (9)

Cand , exponentiala se anuleaza si obtinem rezultatul:

,

care mai poate fi integrat o data in raport cu timpul, conducand la legea lui Einstein:

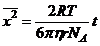   (10)

„Deplasarea patratica medie a unei particule browniene intr-o suspensie data este proportionala cu timpul, daca temperatura ramane constanta”.

Deplasarea patratica medie este invers proportionala cu dimensiunea particulei si este proportionala cu temperatura.

Modul de lucru

Cu ajutorul microscopului cu sistem video de preluare a imaginilor vizualizam pe monitor miscarea browniana a particulelor de fum din camera cu fum.

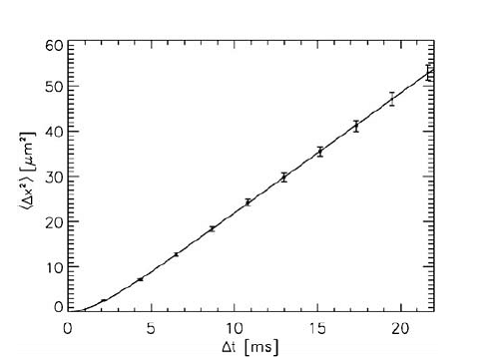
Cu ajutorul appletului putem calcula pentru intervale egale de timp deplasarea unei particule. Reprezentam grafic in functie de t si fitam liniar pentru a determina panta dreptei. Reprezentam grafic in functie de masa particulei, pentru un t fixat;

Reprezentam grafic in functie de T (temperatura) pentru un t fixat.

Consideram miscarea unidimensionala (pe axa Ox) a unui om beat care se intoarce acasa. Consideram ca ocupa pozitia x = 0 la t = 0 si x(t) la momentul t. Consideram ca paseste dupa fiecare interval τ, astfel incat numarul de pasi la momentul t este n = t/τ. De asemenea, consideram ca fiecare pas are lungimea L si ca probabilitatea de a pasi inainte sau inapoi este aceeasi (1/2), pasii succesivi fiind independenti unul de celalalt. Sa se afle pozitia betivului la momentul t.