Marimi relative

Marimi relative

Ponderea persoanelor de sex masculin ori cu studii superioare în totalul anga­jatilor unei firme, numarul de studenti la 1000 de locuitori ori gradul de reali­zare a productiei programate a unei companii, reprezinta doar câteva exemple din aceasta prima categorie de indicatori derivati, prin care se ca­rac­terizeaza, cu ajutorul expresiilor numerice, fenomenele de masa.

Marimile relative au un continut real si se pot exprima în unitati concrete de masura, în coeficienti, procente etc. Ele trebuie terminate astfel încât între indi­catorii aflati la numitorul &# 626f52g 351;i la numaratorul raportului sa existe compara­bilitate si corespondenta logica. Forma generala a unei marimi relative este:

unde: z reprezinta indicatorul relativ;

x reprezinta indicatorul comparat;

y reprezinta indicatorul baza de comparatie;

k reprezinta un numar întreg ce poate fi egal cu:

k=0 si atunci exprimarea se face în coeficienti, iar rezultatul ne arata câte unitati din indicatorul comparat revin la o unitate din indicatorul baza de comparatie;

k=2 si atunci exprimarea se face în procente (%), rezultatul aratând câte unitati din indicatorul comparat revin la o suta de unitati din indicatorul baza de comparatie;

k=3, k=4, k=5 se folosesc atunci când indicatorul comparat este mult prea mic fata de indicatorul baza de comparatie si pentru a mari expresivi­tatea rezultatului exprimarea se face în promile (⁰/₀₀), respectiv prodecimile (⁰/₀₀₀) si procentimile (⁰/₀₀₀₀).

Daca în cadrul unei marimi relative se compara doi indicatori cu continut diferit, dar aflati în relatie de interdependenta, rezultatul are unitate concreta de masura.

Principalele categorii de marimi relative sunt:

marimi relative de structura;

marimi relative de coordonare;

marimi relative de intensitate;

marimi relative de dinamica;

marimi relative ale planului (prevederilor).

3.2.1. Marimi relative de structura

Se calculeaza sub forma unui raport între parte si întreg, prezentând astfel structura colectivitatilor statistice sistematizate atât dupa variabile cantita­tive cât si dupa variabile calitative. Marimile relative de structura pot fi: greutati specifice (ponderi) si frecvente relative.

Pentru o variabila numerica ce înregistreaza la nivelul unei unitati sta­tistice valoarea x_i, i=, iar la nivelul întregii colectivitati de n unitati statis­tice admite aditivitatea , greutatea specifica (ponderea) este:

(3.2)

sau, exprimata în procente:

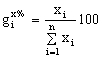(3.3)

si ne arata ponderea nivelului caracteristicii dintr-o unitate în nivelul total al caracteristicii din colectivitatea statistica (exemplu: ponderea veniturilor unei persoa­ne în cadrul veniturilor totale ale familiei).

Daca datele au fost sistematizate pe grupe/clase si s a efectuat centrali­zarea unei variabile numerice atât pe grupe, cât si pentru întreaga colectivi­tate, atunci greutatea specifica este:

(3.4)

sau, pentru exprimarea procentuala:

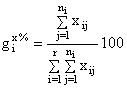(3.5)

unde i= reprezinta numarul grupei/clasei;

n_i reprezinta numarul unitatilor statistice din grupa i (i= )

x_ij reprezinta nivelul variabilei din unitatea j (j = 1, n_i ) si grupa i.

Exemplul nr. 3.1: Pentru trei filiale ale unei firme s au cules si sistemati­zat date privind productia zilnica realizata de muncitori (vezi tab. nr. 3.1)

Tabelul 3.1.

Pentru a determina ponderea productiei obtinute de filiale în cadrul pro­duc­tiei totale a firmei, vom efectua mai întâi centralizarea productiei pe cla­se (filiale) (col. 1, tabelul 3.2) si apoi vom calcula greutatile specifice (col.2, tabelul 3.2):

Tabelul 3.2

În cazul în care datele au fost sistematizate pe variante/intervale de variatie dupa o variabila numerica si cunoastem doar frecventa grupei, n_i , i= si varianta sau centrul intervalului de variatie x_i, i= , atunci greu­tatea specifica a nivelului variabilei dintr-o grupa în nivelul total din colecti­vitate se poate calcula (în ipoteza unei distributii normale a frecventelor pe intervale):

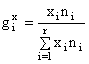(3.6)

sau, în procente:

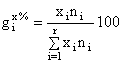(3.7)

Se observa ca suma greutatilor specifice determinate într o colectivitate este întotdeauna egala cu 1, daca exprimarea s-a facut în coeficienti si cu 100%, daca exprimarea s-a facut în procente:

si pentru relatiile (3.2), respectiv

si pentru relatiile (3.4), (3.6), respectiv (3.5),
(3.7)

Tot marimi relative sunt si frecventele relative, despre care am vorbit pe larg în capitolul precedent, calculate pentru seriile de distributie de frec­vente:

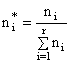(3.8)

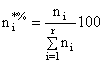(3.9)

si în acest caz, suma frecventelor relative este egala cu 1 sau cu 100 , dupa cum exprimarea s-a facut în coeficienti sau în procente. De aceasta data, însa, marimea relativa nu ne mai arata ponderea nivelului unei caracteristici dintr-o unitate (grupa) în nivelul total al caracteristicii pentru întreaga colectivitate, ci ne arata ponderea unitatilor dintr o grupa/clasa în volumul total al colectivitatii (adica în cele n unitati statistice) (vezi col.3, tabelul 3.2).

Reprezentarea grafica a marimilor relative de structura se face prin dia­grama de structura, prezentata în capitolul anterior, diagrama care poten­tea­za informatiile obtinute prin analiza marimilor relative de structura.

Marimile relative de structura ne arata, asadar, raportul în care se afla di­fe­ritele parti fata de întreg, iar determinarea lor poate oferi multiple valente în cunoasterea statistica.

3.2.2. Marimi relative de coordonare

Se calculeaza ca un raport între doua niveluri ale aceluiasi indicator sta­tistic, niveluri situate pe aceeasi treapta de agregare: unitate, grupa, colecti­vi­tate sta­tistica. Asadar, daca în cazul marimilor relative de structura, rapor­tul se calcula ca parte/întreg, în cazul marimilor relative de coordonare compararea se face sub forma parte/parte sau întreg/întreg. Se pot compara nivelurile unei variabile înregistrate (agregate) în doua unitati diferite, în doua grupe ori în doua colec­tivitati diferite, astfel:

(3.10)

Rezultatul ne arata de câte ori este mai mare (daca rezultatul este suprau­nitar), sau mai mic (daca rezultatul este subunitar) nivelul variabilei în unitatea (grupa, colectivitatea) i fata de nivelul variabilei în unitatea (grupa, colectivi­tatea) j. Nivelul baza de comparatie (la numitor) trebuie ales cu precautie pentru a permite caracterizarea corecta a fenomenelor studiate: uzual nivelul cel mai putin performant, cel mai performant, ori din unitatea (grupa, colectivitatea) în care conditiile generale sunt cele mai stabile.

Folosite îndeosebi în analiza seriilor teritoriale, marimile relative de coor­do­nare admit, în general, reversibilitatea (în functie de pozitia pe care ne situam în analiza), adica se poate calcula si:

, evident cu

Exprimarea rezultatului marimii relative de coordonare (numita si raport de coordonare) se poate face si în procente si atunci ne arata la cât la suta se situeaza nivelul variabilei dintr-o unitate (grupa, colectivitate) fata de ni­velul variabilei din alta unitate (grupa, colectivitate).

Reprezentarea grafica a marimilor relative de coordonare se face prin inter­mediul diagramei prin benzi, coloane ori suprafete.

Exemplul nr. 3.2: Pe baza datelor din tabelul 3.1, col. 1 si din tabelul 3.2, col.1, vom calcula raportul de coordonare pentru numarul de muncitori si pentru productia realizata pe filiale, fata de filiala B (vezi tab. nr. 3.3)

Tabelul 3.3

Se observa, de pilda, ca în filiala A, cu un numar de muncitori de 1,33 ori mai mare decât în filiala B, s a obtinut o productie de 1,53 ori mai mare, ceea ce releva o productivitate a muncii mai crescuta în aceasta filiala, aspect desprins, de altfel, si din analiza marimilor relative de structura, pe baza carora observam ca, în filiala A, 30,77% din muncitori realizeaza 33,09% din volumul productiei.

3.2.3. Marimi relative de intensitate

Sunt singurele marimi relative în care se compara, sub forma de raport, doi indicatori cu continut diferit, dar aflati în interdependenta. Tocmai de aceea, uzual, au unitate concreta de masura (ca de pilda eficienta folosirii capitalului fix, calculata, în forma directa, ca raport între productia obtinuta si capitalul fix folosit si exprimata în lei productie la 1000 lei capital fix).

Marimile relative de intensitate au forma generala:

(3.11)

Ele, evident, nu se pot agrega la nivelul întregului prin însumare, fiind calculate ca ra­poarte cu numitori diferiti. Putem determina, însa, la nivelul întregului (alcatuit din unitati, grupe etc.):

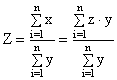(3.12)

si vom vedea, în paragraful urmator ca în acest fel, la nivel de ansamblu, ma­rirea relativa de intensitate are caracter de medie.

Reprezentarea grafica a marimilor relative de intensitate se face cu ajuto­rul diagramelor prin coloane, prin benzi ori prin suprafete.

Exemplul nr. 3.3: Pe baza datelor din tabelul 3.1, col.1 si tabelul 3.2, col.1, putem calcula productia obtinuta de un muncitor (bucati pe muncitor), indicator relativ de intensitate ce are sens de productivitate a muncii (vezi tab. nr. 3.4):

Tabelul 3.4

3.2.4. Marimi relative de dinamica

Sunt folosite pentru analiza evolutiei în timp a fenomenelor social econo­mice supuse studiului statistic si sunt, ca forma generala, un raport între nivelul unei variabile înregistrata într-o perioada (la un moment) de timp si nivelul aceleiasi variabile, situata pe aceeasi treapta de agregare, înregistrata într-o perioada (moment) anterioara (anterior), numita si perioada (moment) de baza. Daca notam nivelul variabilei pentru o grupa, unitate, clasa i, în perioada de baza cu x_0i si nivelul din perioada pentru care facem analiza (numita si perioada curenta) cu x_1i , atunci marimea relativa de dinamica, numita si indice de dinamica este:

(3.13)

sau, în exprimare procentuala:

(3.14)

De remarcat ca, la nivel totalizator (de întreg), nu putem niciodata însuma indicii, ci calculam indicii într-una din variantele:

(3.15)

sau:

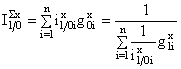(3.16)

unde g_0i^x si g_1i^x reprezinta marimile relative de structura, pentru variabila X, în perioada de baza, respectiv curenta. Evident, pentru o exprimare procen­tuala, rezultatele se înmultesc cu 100.

Reprezentarea grafica a marimilor relative de dinamica se poate face prin diagrama prin coloane, benzi, ori suprafete. Datorita valentelor de cunoas­tere statistica pe care le ofera, dar si particularitatilor, aceste marimi relative vor fi, mai pe larg, tratate în capitolele destinate seriilor de timp (cronolo­gice) si indi­cilor.

3.2.5. Marimi relative ale planului (prevederilor)

Acesti indicatori relativi sunt necesari în activitatile economico sociale, pe de o parte pentru a compara nivelul prevazut al unei variabile cu nivelul realizat într-o perioada anterioara, iar pe de cealalta parte, pentru a compara nivelul efectiv realizat în perioada supusa analizei cu nivelul prevazut (programat).

Astfel, daca notam nivelul unei variabile, realizat într-o perioada anteri­oara, la nivelul unitatii (grupei, clasei) cu x_oi, nivelul programat (planificat sau previzionat) pentru perioada de referinta cu x_pi si nivelul efectiv realizat în perioada de referinta (de analiza) cu x_1i, putem calcula doua marimi relative ale prevederilor:

marimea relativa (indicele) sarcinii programate:

(3.17)

sau în expresie procentuala:

(3.18)

si marimea relativa (indicele) realizarii prevederilor (progra­mu­lui):

(3.19)

sau în expresie procentuala:

(3.20)

Calculul marimilor relative ale prevederilor la nivelul colectivitatii se face similar cu cel al marimilor relative de dinamica.

De asemenea, se observa ca:

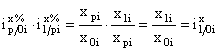(3.21)

Reprezentarea grafica a marimilor relative ale prevederilor se face cu aju­to­rul diagramei prin coloane, benzi ori suprafete. Deseori, atât calculul cât si re­prezentarea grafica a marimilor relative de dinamica si ale prevederilor se face concomitent, în analiza eforturilor si performantelor realizate în diverse activitati social economice.