Miscarea. Elementele miscarii
3.1.Sisteme de referinta. Pozitia punctului material
Pentru studierea deplasarii punctului material este nevoie sa cunoastem traiectoria.
Traiectoria este succesiunea de pozitii pe care mobilul le ocupa in decursul miscarii.
Iar pozitia o putem cunoaste prin raportare la un punct, considerat fix.
Alegem asadar un sistem de coordonate.
Un sistem de coordonate 656c25g este reprezentat de un reper spatial considerat fix precum si de un ceasornic.
Reperul considerat fix ne permite sa determinam
pozitia spatiala a punctului material, iar ceasornicul ne permite sa determinam
momentul temporal. Pozitia se poate
atunci exprima prin vectorul de pozitie
![]() :
:
Vectorul de pozitie este o lungime si marimea lui se exprima in metri.
![]()
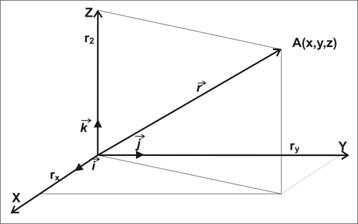
Fig.3.1 Vectorul de pozitie
In cazul unui sistem cartezian, rectangular, (Oxzy) vectorul de pozitie se exprima ca in relatia (3.1)
![]() ) (3.1)
) (3.1)
Aici x, z, y, (sau
![]() ) se numesc
componentele vectorului
) se numesc
componentele vectorului ![]()
![]() iar
iar ![]()
sunt versorii (sau vectorii unitari ) ai celor trei axe x, y, si z. Vezi anexa I.
Exista situatii in care este mai convenabila folosirea unor sisteme de referinta cu alte coordonate decat cele carteziene (x,y,z) - sistemele de coordonate cilindrice (r,θ,z), sferice (r,θ,φ) s.a. figurate in Fig.3.2.
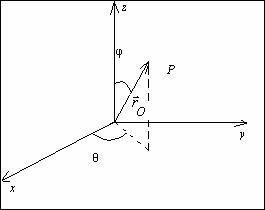
Fig.3.2.
Sistemul de coordonate cilindrice (![]() ,θ,
φ)
,θ,
φ)
Definitie.Viteza punctului material se obtine prin calculul variatiei in timp a vectorului de pozitie:
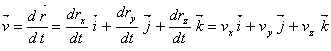 (3.2)
(3.2)
Definitie. Acceleratia miscarii punctului material este data de derivata dupa timp a vitezei punctului material sau de derivata a doua dupa timp a vectorului de pozitie:
![]() (3.3)
(3.3)
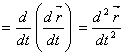 (3.4)
(3.4)
Definitie
Impulsul punctului material este reprezentat de produsul intre masa punctului material si viteza lui:
![]() (3.5)
(3.5)
Impulsul este o marime vectoriala.
Deoarece in mecanica clasica (sau mecanica galileeana, sau newtoriana, sau a vitezelor mici, cum vom vedea la capitolul de mecanica relativista) masa punctului material este constanta, putem scrie:
![]()
Daca aplicam derivarea asupra impulsului obtinem forta.
![]() (3.6)
(3.6)
Ultimele doua egalitati din sirul de relatii (3.6) reprezinta legea a doua a lui Newton sau legea fundamentala de mecanicii.
Mometul fortei
Se poate defini momentul fortei prin relatie :
![]()
Momentul cinetic
Momentul cinetic al unui punct material P fata de un punct fix O este dat prin definitie de relatia:
![]() (3.7)
(3.7)
INTREBARI
1. Traiectoria unui mobil este:
a) drumul parcurs de un mobil in timpul deplasarii sale,
b) succesiunea de pozitii ale unui mobil,
c) expresia matematic a legaturii dintre pozitiile succesive ocupate de un mobil si variabila timp,
d) succesiunea punctelor atinse de varful vectorului de pozitie al unui punct material aflat in deplasare,
e) o marime care caracterizeaza deplasarea unui mobil.
2. ![]() sunt:
sunt:
a) componentele vectorului de pozitie,
b) vectori unitari ai axelor de coordonate rectangulare,
c) versorii celor trei axe,
d) notatii fizice fara o importanta deosebita,
e) versorii axelor de coordonate cilindrice.
3. Privind relatiile de definitie ale momentului fortei si momentului cinetic, in care dintre aceste relatii se afla acceleratia si in care se afla viteza punctului material?
a) acceleratia este continuta in relatia momentului fortei, viteza este continuta in relatia momentului cinetic,
b) ambele relatii contin numai acceleratia, viteza nu este continuta de nici una dintre relatii,
c) ambele relatii contin numai viteza, acceleratia nu este continuta de nici una dintre relatii,
d) acceleratia este continuta in relatia momentului cinetic, viteza este continuta in relatia momentului fortei,
e) relatiile momentului fortei si momentului cinetic nu contin nici viteza si nici acceleratia punctului material.
|