NOTIUNI INTRODUCTIVE GIROSCOP

NOTIUNI INTRODUCTIVE GIROSCOP

Notiuni introductive de teoria giroscopului

Termenul de giroscop vine din limba greaca, giros = rotatie iar scopein = a observa, este vorba deci despre un aparat care permite observarea miscarii de rotatie.

Aparatele giroscopice utilizate la bordul aeronavelor au devenit, in ultimii ani, tot mai complexe din punct de vedere constructiv. Alaturi de componentele de mare precizie, in giroscoapele moderne si-au gasit aplicatii multiple cele mai noi componente electrotehnice si electronice.

Aceste perfectionari constructive sunt o consecinta directa a faptului ca s-a largit considerabil domeniul de utilizare al giroscopului la bordul aeronavelor atat ca aparate care furnizeaza diverse informatii echipajului, cat si ca elemente de automatizare a aparatelor de zbor.

Giroscoapele se utilizeaza pentru masurarea inclinarilor, directiilor, vitezelor unghiulare, acceleratiilor liniare si unghiulare, cuplurilor, vibratiilor, etc.

O alta utilizare a giroscoapelor este aceea din sistemele automate, ca elemente integratoare si derivatoare. Si 737c22h stemele giroscopice au o larga utilizare in pilotarea automata a aeronavelor, in navigatia aeriana si maritima, in dirijarea rachetelor si a vehiculelor spatiale, in stabilizarea miscarii aparatelor aerospatiale, in navigatia inertiala, etc.

Giroscopul este un corp rigid greu cu punct fix avand simetrie de revolutie in repartitia masei, care executa o miscare de precesie regulata cu viteza unghiulara de rotatie proprie orientata in lungul axei de simetrie de revolutie.

Giroscopul integrat cu motorul electric de actionare formeaza asa numitul giromotor. Exista giromotoare de curent continuu si giromotoare de curent alternativ, acestea din urma fiind mai raspandite datorita fiabilitatii superioare.

Pentru a obtine un moment de inertie cat mai mare la acelasi gabarit al aparatului, giromotorul este un motor electric de constructie inversata: rotorul este exteriorul statorului.

Miscarea de rotatie a giroscopului poate fi imprimata si de un motor pneumatic. Suspensia giroscopului intr-un punct fix se obtine cu ajutorul a doua inele articulate, acestea formand asa numita suspensie cardanica exterioara, asigurand giroscopului doua grade de libertate de rotatie.

La unele giroscoape mai speciale se preteaza folosirea suspensiei cardanice interioare care se mai numeste si samiera cardanica sau articulatie Hooke, daca centrul de masa al giroscopului coincide cu punctul de suspensie, giroscopul se numeste giroscop perfect centrat sau astatic.

Un giroscop perfect centrat asupra caruia nu actioneaza momente exterioare se numeste giroscop liber. Un giroscop al carui centru de masa nu coincide cu punctul de suspensie se numeste giroscop greu.

Daca unul din cele doua inele de suspensie este blocat se obtine asa numitul giroscop cu un grad de libertate, acesta avand multiple aplicatii in aparatele de bord.

Prezenta inelelor de suspensie are o serie de implicatii asupra functionarii aparatelor giroscopice, datorita lor se produc erorile cardanice care se analizeaza concret pentru fiecare tip de aparat giroscopic.

In afara de giroscop, giromotor si inele de suspensie, aparatele giroscopice contin multe alte componente cum ar fi:

lagarele de suspensie;

motoare de corectie;

elemente sensibile;

traductoare de diferite categorii;

selsine;

sisteme de urmarire;

blocuri de calcul.

O atentie deosebita se acorda influentei frecari in lagare asupra preciziei aparatelor giroscopice, de regula se utilizeaza lagare de rulare speciale. Lagarele principale, adica acelea care asigura rotatia in jurul axei 3, trebuie sa reziste la turatii foarte mari ale miscarii proprii de rotatie

(12000 30000rot/min).

Spre deosebire de acestea lagarelel inelelor de suspensie lucreaza la viteze foarte mici de rotatie, lor li se impune conditia de a avea momente de frecare foarte mici si jocuri axiale si radiale extrem de reduse.

Suspensia giroscopului intr-un punct fix cu articulatie cardanica exterioara

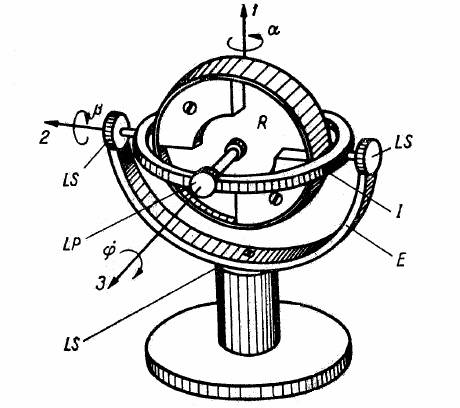
Fig. 1

LP - lagar principal

LS - lagarele inelelor de suspensie

I - interior

E - exterior

Giroscop cu suspensie Hooke (interioara)

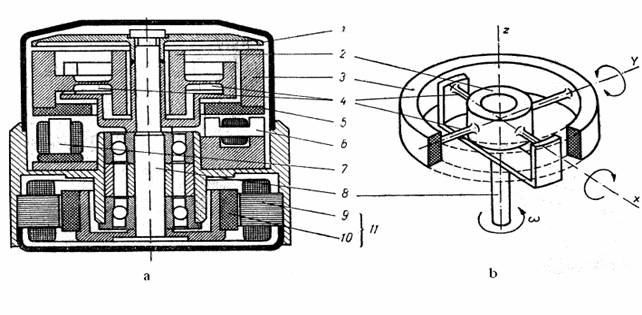
Fig. 1.2

a - constructia giroscopului

b - schema cinematica

1 - disc

2 - inel interior

3 - volant

4 - bare de torsiune

5 - armatura magnetica

6 - traductoare inductive

7 - motoare de cuplu ( de precesie )

8 - arborele de antrenare

9 - stator

10 - rotor

11 - motor sincron

Modelul mecanic al giroscopului

Definitia data anterior giroscopului justifica incadrarea acestuia in conditiile cazului Lagrange - Poisson tinand cont ca viteza unghiulara de rotatie are modulul cu mult mai mare decat modulul vitezei de precesiei . Legatura ce imobilizeaza punctul in jurul caruia se executa precesia regulata se asimileaza cu un grad de tip articulatie sferica cu frecare neglijabila (fig. 1.3) si avand conditiile cinematice suplimentare:

In conditiile de mai sus momentul cinetic raportat la polul fix are expresia:

,

aceasta reprezentand ipoteza fundamentala a teoriei elementare a giroscopului.

Avand in vedere ca momentul fortelor pasive nul, ca urmare a neglijari frecarii in articulatia sferica si tinand seama de ultimele doua expresii, expresia momentului fortelor active raportat la polul fix devine:

Aceasta ecuatie reprezinta ecuatia fundamentala a teoriei elementare a giroscopului.

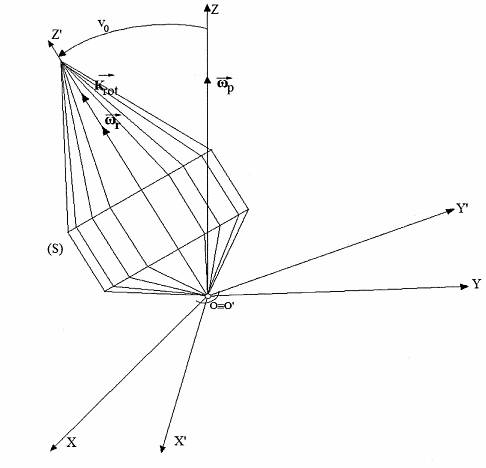
Fig. 1.3

Fenomene giroscopice

In cazul giroscoapelor apar urmatoarele fenomene caracteristice:

stabilitatea axei giroscopului;

efectul giroscopic;

cuplul giroscopic;

miscarea de precesie.

Stabilitatea axei giroscopului consta in mentinerea axei de rotatie proprii atunci cand asupra giroscopului nu actioneaza forte perturbatoare exterioare, fenomen care este des utilizat in aplicatiile practice.

In cazul giroscopului liber momentele active sunt nule:

Tinand seama ca s-au neglijat frecarile, rezulta ca momentele pasive sunt nule:

Deoarece giroscopul prezinta simetrie de revolutie in repartitia masei, sunt indeplinite urmatoarele conditii:

,

obtinandu-se sistemul:

integrand

unde este viteza unghiulara initiala.

Inlocuind in sistem si eliminand intre acestea se obtine:

in care:

Solutia ecuatiei diferentiale este:

Semnul ( + ) corespunde cazului iar semnul ( - ) cazului

Daca la momentul initial viteza unghiulara este orientata in jurul axei OZ', atunci si deci . De aici rezulta ca in timpul miscarii avem:

In cazul perturbatiilor initiale mici , constantele si au si acestea la randul lor valori mici.

Astfel, si au valori mici in timpul miscarii si deci vectorul de rotatie unghiulara proprie are abateri mici fata de axa giroscopului.

Perioada perturbatiilor coincide cu perioada functiilor si si cu cat aceasta este mai mica cu atat giroscopul este mai stabil:

Giroscopul liber este cu atat mai stabil cu cat forma lui este mai alungita pe si cu cat viteza unghiulara initiala este mai mare.

Efectul giroscopic

Efectul giroscopic consta in rotirea axei giroscopului atunci cand asupra acestuia actioneaza un cuplu de forte perturbatoare exterioare, fenomenul aparand la toate giroscoapele centrate sau necentrate.

Considerand un giroscop antrenat in miscarea de rotatie cu viteza unghiulara initiala orientata in lungul axei de rotatie proprie , vectorul moment cinetic raportat la centrul de masa este, de asemenea, orientat dupa aceeasi axa (fig. 1.4).

In acest caz expresia momentului cinetic este urmatoarea:

Cand este suficient de mare si imprima giroscopului o miscare de rotatie cu viteza unghiulara , viteza unghiulara rezultata devine:

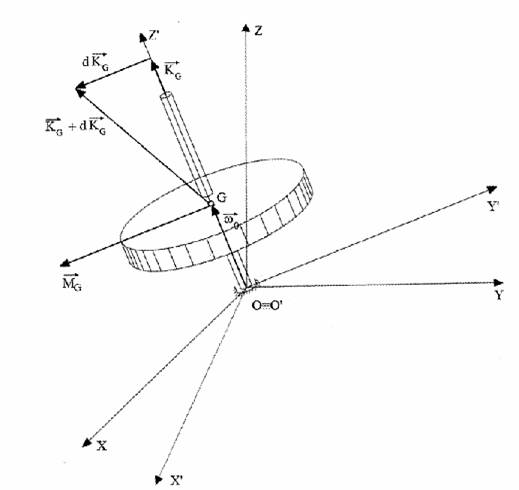
Fig. 1.4

Proiectiile vectorului pe axele sunt:

Proiectiile vectorului momentului cinetic rezultant sunt:

Componentele sunt mult mai mici decat componenta deoarece

Vectorul moment cinetic v-a devia foarte putin fata de axa a giroscopului.

La imprimarea unei viteze unghiulare suplimentare , in conditiile in care este suficient de mare, efectul giroscopic este mic.

Aplicand axei giroscopului un cuplu de forte situat in planul apare un moment orientat dupa axa . In aceasta situatie fortele aplicate pot perturba sau nu miscarea giroscopului.

In cazul in care fortele aplicate nu perturba miscarea axei giroscopului, momentul produce intr-un interval de timp o variatie a momentului cinetic care conform teoremei momentului cinetic are expresia:

Vectorul momentului cinetic rezultant este situat in planul , astfel axa de rotatie proprie a giroscopului va avea o noua orientare, dupa directia momentului cinetic rezultant.

Astfel, axa giroscopului se va roti intr-un plan perpendicular pe planul fortelor perturbatoare aplicate ( efectul giroscopic ).

Miscarea de precesie

Sub actiunea greutatii proprii ( giroscopul liber ) si eventual sub actiunea altor forte exterioare apare o deviatire a axei giroscopului. Aceasta deviatie determina o miscare de revolutie a axei giroscopului in jurul axei care se suprapune peste miscarea de rotatie proprie, rezultanta celor doua miscari reprezentand miscarea de precesie.

Pentru descrierea miscarii de precesie se considera un punct semnificativ al giroscopului si anume extremitatea libera a sa, curba descrisa de acest punct este situata pe o sfera de raza intre paralelele si si fiind valorile, minima si respectiv maxima a unghiului de nutatie (fig. 1.5).

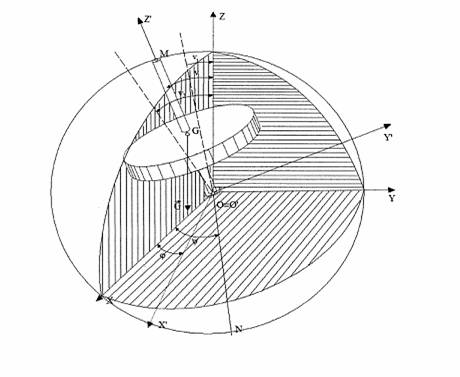
Fig. 1.5

Unghiul de nutatie variaza in timp ca si cand sistemul ar avea un singur grad de libertate, caz in care energia sa totala si energia sa potentiala sunt:

unde:

Exprimand in functie de si avem:

Energia totala a sistemului este:

Notand , legea de conservare a energiei se poate scrie:

unde:

iar legea de variatie a unghiului de rotatie proprie

Unghiul are o variatie periodica intre doua valori limita si , variatie ce poarta numele de nutatie (fig. 1.6)

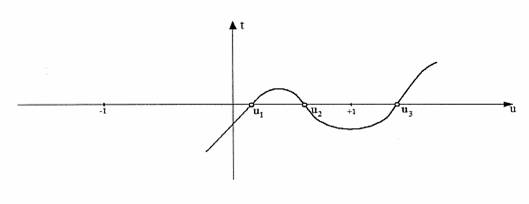
Fig. 1.6

Cuplul giroscopic

Consideram un giroscop care se roteste cu viteza unghiulara initiala si ca asupra lui actioneaza o forta exterioara care creeaza un cuplu perturbator

In lagarele axei giroscopului apare o forta de reactie numita rectiune giroscopica (fig. 1.7).

Aceasta forta creeaza un cuplu de reactiune:

cuplul giroscopic.

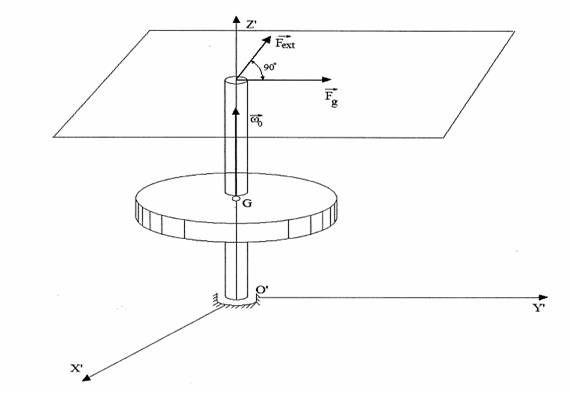
Fig. 1.7

1.4 Tipuri de giroscoape

In functie de unele particularitati constructive si de unele aproximari in ceea ce priveste miscarea, giroscoapele pot fi clasificate in urmatoarele categorii:

a)      giroscoape centrate sau necentrate:

giroscopul centrat este un giroscop al carui punct fix coincide cu centrul sau de masa;

giroscopul necentrat este un giroscop la care centrul de masa se afla situat pe axa acestuia.

b)      giroscoape libere:

giroscoape centrate asupra carora actioneaza numai greutatea proprie.

c)      giroscoape lente sau rapide:

giroscopul lent este giroscopul a carui axa de rotatie proprie este foarte apropiata de axa si a carui viteza unghiulara este constanta

giroscopul rapid este giroscopul a carui energie cinetica este mult mai mare decat energia sa potentiala

d)      giroscoape usoare sau grele:

giroscopul usor este un giroscop ce are o greutate proprie mica;

giroscopul greu este un giroscop necentrat avand greutate mare si centrul de masa situat pe axa sa de rotatie. Actiunea greutatii conduce la cresterea unghiului de nutatie . Axa giroscopului descrie o suprafata conica avand unghiul la varf (fig. 1.8).

e)      giroscoape simetrice sau asimetrice:

giroscopul simetric este un giroscop cu simetrie de revolutie in repartitia

masei . Toate giroscoapele de mai sus sunt giroscoape simetrice.

giroscopul asimetric este un giroscop a carui masa este uniform distribuita atat in lungul axei sale cat si radial.

Ca urmare cele trei momente de inertie axiale sunt diferite intre ele:

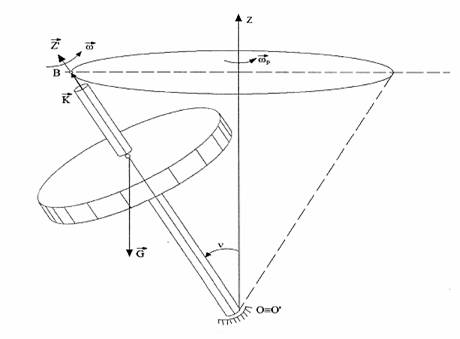
Fig. 1.8

1.5 Clasificarea aparatelor giroscopice

Clasificarea aparatelor giroscopice din punct de vedere functional, in functie de parametrii masurati de aparatele giroscopice:

a)      Aparate giroscopice pozitionale sau de memorare a unei directii date, utilizeaza

proprietatea giroscopului liber de a-si mentine neschimbata orientarea in spatiu a momentului cinetic. De regula pozitiile memorate sunt verticala locului si directia meridianului geografic, care, nefiind fixe se rotesc datorita rotatiei Pamantului si deplasarii aeronavei, rezultand un giroscop nesatisfacator. Acesta trebuie prevazut cu un sistem de corectie fie de tip pendular ( pentru giroscopul de verticala ), fie un traductor de camp de camp magnetic ( pentru giroscoapele de directie ).

b)      Compasurile giroscopice, reprezinta clasa de aparate giroscopice la care axa de rotatie

proprie, are capacitatea de a se orienta in azimut, ca urmare a deplasarii centrului de masa fata de punctul de suspensie ( aparatele nu au sistem de corectie ).

c)      Stabilizatoarele giroscopice, se impart in doua grupe:

stabilizatoare giroscopice directe, stabilizatorul serveste ca element de forta ce asigura stabilizarea impusa unui dispozitiv de bord;

stabilizatoare giroscopice indirecte, giroscopul este folosit ca element de masurare.

d)      Giroscoapele de viteza, care mai sunt numite si girometre sunt folosite la masurarea vitezei unghiulare de rotatie a unei aeronave in jurul axelor sale.

Aceste giroscoape sunt foarte des intalnite in sistemele de comanda automata a aeronavelor, existand mai multe tipuri de giroscoape de viteza:

girotahometre;

giroscoape de derivare;

giroscoape de integrare simpla sau dubla.

e)      Alte tipuri de aparate giroscopice:

giroscoape integratoare de acceleratie liniara;

giroaccelerometre;

giroscoape de comanda;

relee giroscopice;

giroscoape cu vibratii.