Obiectul fizicii. Legatura fizicii cu celelalte stiinte si cu tehnica. Dezvoltarea fizicii in Romania. Marimi fizice si unitati de masura. Analiza dimensionala
1.1 Introducere
Cuvantul fizica este de origine greaca (physis=natura). Denumirea a fost data de Aristotel, semnificand faptul ca fizica este o stiinta a naturii. Desi era o personalitate proeminenta a lumii antice, totusi in domeniul fizicii toate ideile sale s-au dovedit a fi gresite, exceptand denumirea data stiintei respective.
Obiectul fizicii il constituie studierea structurii materiei, a proprietatilor ei generale si a formelor sale de miscare (mecanica, termica, cuantica, nucleara etc.), a transformarilor reciproce ale acestor forme de miscare.
Dezvoltarea stiintelor si a tehnicii nu poate fi conceputa astazi fara dezvoltarea si aprofundarea cunostintelor la disciplina fizica, precum si la celelalte discipline fundamentale ca matematica, chimia, biologia. Astfel, unele legi descoperite initial la chimie au precedat formularea unor legi ale fizicii. Ca un exemplu, legile proportiilor simple sau multiple au condus la ideea discontinuitatii materiei, inspirandu-l pe Avogadro sa formuleze legea volumelor la fizica moleculara. Pot fi date mai multe exemple in care dezvoltarea uneia dintre stiintele fundamentale a influentat dezvoltarea celorlalte: aparitia calculului diferential si integral la matematica, teoria relativitatii sau teoria cuantelor la fizica, biofotonica etc.
In tara noastra fizica s-a bucurat dintotdeauna de o atentie deosebita, unii fizicieni romani aducand contributii importante la dezvoltarea acestei discipline, atat pe plan national cat si international. Cei mai importanti dintre acestia sunt:
Dragomir Hurmuzescu (1865-1954) a efectuat cercetari in domeniul electricitatii si fizicii radiatiilor Roëntgen, a construit electroscopul care ii poarta numele, a masurat constanta electrodinamica.
Stefan Procopiu (1890-1972), fizician de renume mondial s-a ocupat, pe langa activitatea didactica, si de cercetarea stiintifica. A stabilit printr-un rationament ingenios, pentru prima data in lume, valoarea momentului magnetic molecular sau magnetonul teoretic, in anul 1912, cand era inca student. Nu i s-a acordat Premiul Nobel pentru aceasta descoperire dintr-o neglijenta a comisiei. In anul 1921 a descoperit fenomenul depolarizarii luminii de catre suspensii si coloizi (fenomenul Procopiu), iar in 1930 a descoperit efectul Procopiu, care consta in efectul circular al discontinuitatilor magnetice. A fost desemnat de doua ori in comisia pentru nominalizari la premiul Nobel.
Ion Agarbiceanu (1907-1971) a fost profesor la Institutul Politehnic Bucuresti, avand cercetari in domeniul fizicii atomice si spectroscopiei. In anul 1962 a fost construit sub conducerea sa, la Institutul de Fizica Atomica din Bucuresti-Magurele, primul laser cu gaz din tara si unul dintre primele din lume.
Horia
Hulubei
(1896-1972) a fost profesor la Universitatea Bucuresti, bucurandu-se de aprecierea
marilor savanti ai vremii. S-a remarcat prin lucrari in domeniul spectroscopiei
optice, de raze ![]() si
si ![]() , si in domeniul fizicii nucleare.
, si in domeniul fizicii nucleare.
Eugen Badarau (1887-1975) a fost profesor la Universitatea Bucuresti si academician. A avut lucrari importante in domeniile opticii, spectroscopiei si acusticii, A initiat cecetari asupra descarcarilor electrice in gaze si plasmei in Romania, a explicat mecanismul descarcarilor luminiscente in arc.
1.2 Metode de cercetare in fizica
Fizica a devenit o stiinta de sine statatoare in perioada de dupa Renasterea italiana, cand metoda experimentala de studiu promovata de Galileo Galilei a relevat aspectele profunde ale unor fenomene din natura. Galilei a fost primul care a tinut sa verifice experimental legi si postulate considerate valabile apriori, ca de exemplu caderea libera a corpurilor. Prin utilizarea planului inclinat, Galilei reducea acceleratia de cadere, marind astfel timpul de masurare a distantelor. De atunci se spune ca "stiinta a coborat din Cer pe Pamant pe planul inclinat al lui Galilei".
In secolele XVII-XVIII s-a realizat prima impartire a fizicii pe ramuri, cristalizandu-se in sec XIX ramurile clasice: mecanica, termodinamica, electricitatea si optica. In aceasta perioada incepe sa fie utilizata si metoda teoretica de studiu, bazata pe metodele matematicii clasice. Teoriile fizicii s-au dezvoltat in doua directii:
- fenomenologica, care porneste de la proprietatile macroscopice ale corpurilor;
- microscopica, care porneste de la structura interna a corpurilor.
Teoriile sunt considerate concludente daca prin aplicarea fiecareia dintre cele doua metode se obtin rezultate identice in studierea unui fenomen.
In sec. IX-XX au aparut ramurile moderne ale fizicii: fizica particulelor elementare, fizica atomului, solidului, plasmei, mecanica cuantica etc.
Teoriile fizicii moderne pornesc de la ipoteze asupra structurii intime a corpurilor, care prin interpretari matematice devanseaza realizarile practice bazate pe teoriile respective. Intervalul de timp de la o descoperire la aplicatia practica bazata pe aceasta a scazut constant o data cu trecerea timpului. Astfel, de la descoperirea fisiunii nucleare in anul 1934 pana la construirea primului reactor nuclear au trecut 8 ani, iar de la formularea teoriei tranzistorilor pana la realizarea lor au trecut numai 3 ani (1951). In prezent, in tarile dezvoltate acest interval de timp a scazut pana la ordinul zilelor, datorita progresului tehnologic si concurentei acerbe pe piata produselor de inalta tehnologie.
Inainte de perioada comunismului, in tara noastra fizica s-a dezvoltat datorita unor personalitati stiintifice recunoscute de comunitatea internationala, care au studiat in strainatate, fiind in contact cu cercurile stiintifice ale vremii. Cu toate acestea, nu exista o baza de mase, deoarece numai cei din familiile instarite isi puteau permite studii in strainatate. In perioada comunismului s-a creat aceasta baza, creandu-se conditiile pentru dezvoltarea pe orizontala a acestei stiinte, insa fara criterii clare de departajare a valorilor. Aceasta inseamna ca puterea de decizie nu apartinea de obicei persoanelor cele mai competente din punct de vedere stiintific, ci se acorda dupa alte criterii. Cu toate acestea, s-au creat unele conditii pentru dezvoltarea stiintei si promovarea cercetarii fundamentale, insa gestionarea relatiei cu cercetarea aplicativa si productia de bunuri a fost de asemenea deficitara.
In invatamantul superior au fost create primele facultati de fizica prevazute cu sectii de specialitate in aproape toate domeniile fizicii, precum si institute de cercetare (I.C.F.I.Z. in Bucuresti, Institutul de Izotopi Stabili in Cluj, Institutul de Reactori Nucleari din Pitesti etc 616g64g .). Printre domeniile de cercetare-dezvoltate s-au numarat urmatoarele:
- energetica nucleara, cu aplicatii industriale cum ar fi centrala nucleara de la Cernavoda;
- aplicatiile laserilor in industrie (geodezie, prelucrarea materialelor, aliniere, energetica nucleara), biologie (biofotonica), medicina (terapie si chirurgie cu laser, imagistica medicala), informatica (optical computing), tehnica militara (telemetrie laser, sisteme de paza si alarmare, ghidarea proiectilelor in fascicul laser, aparatura de vedere pe timp de noapte) etc.
- fizica materialelor, cu scopul de a crea materiale noi si performante pentru industria electronica, energetica, aeronautica etc.
- optica neliniara, fizica semiconductoarelor s.a.
In special in cursul istoriei recente se pot da numeroase exemple privind rolul stiintei (si al fizicii in special) in influentarea relatiilor internationale, geopolitice, a geografiei, istoriei, a strategiei militare etc. prin impactul pe care l-a avut folosirea unor descoperiri stiintifice. Astfel, al doilea razboi mondial se putea prelungi cu cativa ani datorita rezistentei puternice opuse de trupele japoneze trupelor aliate in Pacific. Aruncarea a doua bombe atomice asupra teritoriului japonez a convins guvernul japonez sa capituleze. In razboiul din Vietnam s-au testat pentru prima data telemetrele cu laser, care asigurau o precizie de lovire de 15 cm la o distanta de 10 km, fapt care s-a dovedit in final insuficient, pentru ca SUA au suferit in final o infrangere umilitoare. In razboiul din insulele Malvine (Falkland) dintre Marea Britanie si Argentina trupele britanice au utilizat in premiera aparatura de vedere pe timp de noapte, ceea ce le-a permis sa obtina capitularea adversarului datorita superioritatii tehnice, desi acesta era mult superior numeric si lupta pe teren propriu.
Din cele discutate se poate desprinde ideea ca fizica este o stiinta experimentala, rezultatele obtinute in procesul de masurare avand un rol fundamental in enuntarea ideilor si a legilor fizicii. Pentru formularea cantitativa a acestor legi se folosesc notiuni si procedee matematice corespunzatoare. In acest sens enumeram cateva idei ale unor savanti despre rolul masurarii in fizica.
William Thompson (lord Kelvin): "Cand putem masura marimea despre care vorbim si o putem exprima printr-un numar, atunci noi stim ceva despre ea; dar cand nu o putem exprima printr-un numar, cunoasterea noastra este slaba si nesatisfacatoare".
D. I. Mendeleev: "Stiinta incepe atunci cand incep masuratorile".
Max Planck, reluand o idee a lui Galilei, indemna pe fizicieni sa masoare tot ce este masurabil si sa faca masurabil tot ceea ce nu este inca masurabil.
1.3 Marimi fizice si unitati de masura
In urma observatiilor si a experimentelor asupra diferitelor sisteme de corpuri, s-a constatat ca acestea prezinta unele proprietati comune cum ar fi: inertia, masa, volumul, culoarea, forma etc. Astfel, multitudinea informatiilor obtinute despre sistemele fizice in procesele de observare directa sau masurare prin intermediul diferitelor instrumente de masura, pot fi grupate in mai multe clase de echivalenta disjuncte. Fiecarei clase i se asociaza o proprietate fizica a corpurilor sau sistemelor de corpuri materiale. Proprietatile fizice ale diferitelor sisteme de corpuri materiale, care pe langa operatia de echivalenta corespunzatoare admit si o operatie de ordonare a elementelor componente, se numesc marimi fizice.
Operatia sau procedeul de ordonare prezinta urmatoarele proprietati:
- asimetria: Daca elementul ![]() este mai mic in raport
cu operatia considerata decat elementul
este mai mic in raport
cu operatia considerata decat elementul ![]() , atunci elementul
, atunci elementul ![]() nu poate fi mai mic
decat
nu poate fi mai mic
decat ![]() in raport cu alta
operatie de ordonare:
in raport cu alta
operatie de ordonare:
![]()
- tranzitivitatea: Daca in raport cu operatia de ordonare adoptata sunt valabile inegalitatile
(![]() si
si ![]() ),
),
atunci aceasta implica si inegalitatea:
![]()
1.4 Simboluri
Pentru exprimarea cat mai simpla a legilor si teoremelor fizicii cu ajutorul formulelor, se folosesc diferite simboluri pentru marimile respective. De asemenea, pentru exprimarea cat mai simpla a rezultatelor unei masuratori se aleg simboluri pentru unitatile marimilor respective si pentru valorile marimilor fata de acele unitati. Simbolul marimii fizice se va scrie ca produsul simbolic dintre valoare si unitatea de masura. Este necesar intotdeauna sa se specifice intr-o formula fizica sensul simbolurilor folosite, adica acela pentru valoare, marime, sau unitate. Daca simbolul folosit reprezinta o valoare, se va specifica si sistemul de unitati. O categorie aparte de simboluri o reprezinta anumite operatii matematice care se efectueaza asupra unor marimi fizice, ca de exemplu operatii aritmetice, vectoriale, operatii de diferentiere si integrare etc.
1.5 Masurarea unei marimi fizice
Fizica studiaza fenomenele din natura cu ajutorul marimilor. Marimile reprezinta acele proprietati fizice ale corpurilor materiale care sunt masurabile. Prin masurare marimea respectiva se compara cu o anumita marime de aceeasi natura, stabilindu-se raportul intre acea marime si marimea cu care se compara. Din punct de vedere al masurabilitatii exista doua grupuri de marimi: direct masurabile si indirect masurabile.
Marimile direct masurabile (marimile fizice propriu zise) sunt acele marimi pentru care se pot defini operatiile de egalitate si adunare, care la randul lor permit efectuarea raportului a doua marimi de aceeasi natura, prin urmare si stabilirea procedeului de masurare. Alegand pentru astfel de marimi marimea unitate, se pot masura direct celelalte marimi prin procedeul stabilit. Exemplele cuprind majoritatea marimilor folosite in fizica: lungimea, masa, energia, unghiul, greutatea etc.
Marimile indirect masurabile sunt acelea pentru care se poate defini numai operatia de egalitate, intrucat adunarea nu are sens fizic. Exemple: temperatura, potentialul electrostatic, altitudinea, densitatea etc. Formarea raportului a doua marimi de aceeasi natura nefiind posibil, aceste marimi pot fi facute totusi masurabile indirect. Pentru aceasta se alege un corp cu proprietati potrivite pentru punerea in evidenta a marimii fizice de masurat si un reper conventional, observand pozitia corpului respectiv fata de reperul dat (de exemplu la masurarea temperaturii se urmareste meniscul alcoolului din tubul capilar al unui termometru).
Definirea egalitatii si adunarii permit trecerea
la definitia raportului a doua marimi de aceeasi natura. De exemplu, raportul a
doua lungimi ![]() si
si ![]() este egal, prin
definitie, cu de cate ori trebuie pusa la cap lungimea
este egal, prin
definitie, cu de cate ori trebuie pusa la cap lungimea ![]() pentru a reproduce o
lungime egala cu
pentru a reproduce o
lungime egala cu![]() , obtinandu-se un numar pentru raportul
, obtinandu-se un numar pentru raportul ![]() . Daca acest numar nu este intreg, se imparte lungimea
. Daca acest numar nu este intreg, se imparte lungimea ![]() intr-un numar din ce
in ce mai mic de parti egale pana cand se poate obtine din aceste fractiuni,
prin punerea lor una in continuarea alteia, o lungime egala cu
intr-un numar din ce
in ce mai mic de parti egale pana cand se poate obtine din aceste fractiuni,
prin punerea lor una in continuarea alteia, o lungime egala cu ![]() . Pentru a trece de la notiunea de raport la notiunea de masurare
este suficient sa alegem printre marimile de aceeasi natura (notate generic cu
. Pentru a trece de la notiunea de raport la notiunea de masurare
este suficient sa alegem printre marimile de aceeasi natura (notate generic cu ![]() ) o anumita marime unitate,
notata cu
) o anumita marime unitate,
notata cu ![]() . Raportul dintre marimea fizica
. Raportul dintre marimea fizica ![]() si unitatea
si unitatea ![]() se numeste valoarea
marimii
se numeste valoarea
marimii ![]() , notata cu simbolul
, notata cu simbolul ![]() :
:
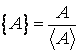
Alegand ca unitate o alta marime ![]() de aceeasi natura, valoarea
marimii
de aceeasi natura, valoarea
marimii ![]() va fi:
va fi:
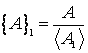 .
.
In consecinta, putem defini masurarea ca fiind compararea marimii de masurat cu o anumita marime unitate (raportul dintre valoarea marimii de masurat si unitatea aleasa).
Un criteriu de clasificare pentru marimile fizice poate fi caracterul pe care il prezinta acestea fata de simetria fenomenelor. Dupa acest criteriu se pot mentiona marimile scalare (masa, densitatea, energia etc.), vectorii (forta, viteza etc.), tensorii de ordinul doi (momentul cuplului de forte, inductia magnetica etc.) si pseudoscalarii (volumul, fluxul inductiei electrice etc.).
Anumite proprietati fizice cum ar fi forma, electronegativitatea, distributia spatiala, nu sunt masurabile. Desi admit o operatie de echivalenta, ele nu se pot ordona in cadrul clasei de echivalenta din care fac parte. Culoarea a fost multa vreme considerata o proprietate si nu o marime fizica, insa o data cu asocierea unei valori a marimii lungime de unda pentru fiecare culoare, in cadrul teoriei electromagnetice a luminii, culoarea a devenit o marime fizica.
Proprietatile fizice ale caror elemente fizice admit o operatie de ordonare, care caracterizeaza starile posibile ale unui corp sau ale unui sistem de corpuri limitat in timp si spatiu, reprezinta parametri fizici ai sistemului respectiv (de exemplu, presiunea si temperatura unui gaz aflat in diferite conditii). Marimile fizice se refera la proprietatile fizice ale tuturor corpurilor sau sistemelor de corpuri din natura, corespunzatoare claselor de echivalenta respective (masa, lungime, presiune etc.).
Prin masurare se atribuie valori individuale (numere), conform unor reguli stabilite, parametrilor sau marimilor fizice care caracterizeaza starile posibile ale sistemelor studiate. O anumita valoare a unui parametru fizic, in conditii date, reprezinta o cantitate fizica sau un element component al parametrului fizic considerat.
Orice marime fizica este caracterizata printr-o latura calitativa si o latura cantitativa. Marimile care exprima aceeasi proprietate calitativa, dar se deosebesc prin latura cantitativa, se numesc marimi de aceeasi natura. Marimile de aceeasi natura pot fi mai mari sau mai mici, mai intense sau mai slabe, ceea ce constituie latura cantitativa a marimii fizice respective. De exemplu, forta caracterizeaza interactiunea dintre doua sau mai multe corpuri si este calitativ diferita de acceleratie, care caracterizeaza modul de variatie a vitezei in timp.
Valoarea unui parametru fizic depinde nu numai de unitatea de masura in care se exprima numarul respectiv, ci si de calitatea procedeului de masurare. Stiinta care se ocupa de mijloacele si procedeele de masura pentru marimile fizice, de unitatile lor de masura si de totalitatea normelor privitoare la folosirea masurilor, a mijloacelor si metodelor de masura pentru toate marimile fizice, se numeste metrologie (de la metros=masurare si logos=a vorbi, a numara, ceea ce se traduce prin stiinta masurarilor), constituind o ramura importanta a fizicii. Perfectionarea tehnicilor de masurare si elaborarea de noi procedee de masura, pe baza acumularii de noi cunostinte in fizica si a dezvoltarii tehnicii, determina ca aceasta stiinta sa fie deschisa. Astfel in zilele noastre este posibila masurarea unor marimi fizice care cu zeci de ani in urma erau considerate nemasurabile (in domeniul fizicii atomice si nucleare, particulelor elementare, spectroscopiei etc.).
Alegerea unitatii de masura nu este impusa de nici o lege a fizicii, ci numai de considerente de ordin practic (exactitate, reproductibilitate, arie mare de acoperire, comoditate in folosire). De asemenea, alegerea unei unitati de masura pentru o marime fizica conduce la stabilirea unitatilor de masura pentru alte marimi fizice. De exemplu, unitatea de masura a vitezei depinde de unitatile de masura pentru spatiu si timp. Se impune rezervarea unui numar minim de marimi fizice independente intre ele, numite marimi fundamentale, astfel ca unitatile de masura pentru toate celelalte marimi fizice sa depinda numai de acestea. Unitatile de masura stabilite pentru marimile fizice fundamentale se numesc unitati fundamentale.
Marimile fizice ale caror unitati se exprima prin combinatii ale unitatilor fundamentale se numesc marimi derivate, iar unitatile lor se numesc unitati derivate. Impartirea marimilor fizice in cele doua categorii este de mare importanta practica, deoarece permite reducerea numarului de unitati pentru care trebuie confectionate masuri standardizate. Acestea reproduc o unitate de marime si se numesc etaloanele marimii respective.
1.6 Relatii intre marimi
Cele mai generale relatii intre marimi sunt legile. Acestea se descopera pe cale experimentala (legea lui Coulomb de la electrostatica, legea lui Newton la mecanica, legea lui Faraday a inductiei electromagnetice) sau pe cale pur teoretica (legea-ecuatia lui Schrodinger la mecanica cuantica, ecuatiile lui Lagrange la mecanica analitica etc.). Principiile sau postulatele se enunta pornind de la constatarea ca toate consecintele ce decurg din acestea sunt verificate experimental; asadar, lucrurile se intampla conform postulatelor, chiar daca nu se stie exact de ce se desfasoara in acest mod. Daca la un moment dat teoria se va completa pe baza unor noi ipoteze rezultate din experimente, este posibil ca unele postulate sa fie demonstrate, si astfel sa devina teoreme sau legi.
Exista si legi cu caracter mai limitat, denumite legi de material, in care intervin marimi caracteristice diferitelor materiale, ca de exemplu legile frecarii, legea difuziei la mecanica, legea lui Hooke la elasticitate, legea polarizatiei electrice de la electricitate. In cazul legii lui Hooke modulul de elasticitate poate depinde de diferiti parametri (presiune, temperatura etc.), furnizand pentru materialele cunoscute un numar mare de legi de material.
Teoremele reprezinta relatii intre marimi care se stabilesc pe cale deductiva din legile de material, folosind metode matematice, ca de exemplu operatori diferentiali, calculul algebric, calculul integral, De exemplu, teorema lui Coulomb de la electrostatica se poate deduce din legea fluxului electric a lui Gauss. Tendinta este ca in timp, prin gasirea unor legi mai generale cu ajutorul fizicii teoretice, numarul legilor sa scada, astfel ca unele dintre acestea sa devina teoreme. De exemplu, legea gazelor ideale a devenit o teorema de cand ea a fost dedusa in fizica statistica plecand de la legile mecanicii, cu utilizarea calculului probabilitatilor de la fizica statistica. De asemenea, legile lui Kirchoff au devenit teoremele lui Kirchoff de cand au fost deduse din legile de conservare pentru energie si sarcina electrica. Este de asemenea de remarcat ca in cadrul unui capitol al fizicii, chiar daca numarul de legi generale ramane constant, sistemul de legi generale se poate schimba. Astfel, la electrostatica legea generala a lui Coulomb poate fi inlocuita de legea lui Gauss, deoarece aceasta este mai generala decat fosta lege a lui Coulomb, care astfel devine teorema.
Relatiile de definitie determina unele marimi
fizice. De exemplu, se defineste densitatea de energie ca raportul dintre
energia ![]() dintr-o zona a spatiului si volumul
dintr-o zona a spatiului si volumul ![]() in care aceasta este
continuta:
in care aceasta este
continuta:
![]()
Avantajul utilizarii simbolului![]() (egal prin definitie) este faptul ca intr-o singura relatie
se poate scrie atat definitia unei marimi, cat si legea care da dependenta
marimii respective de alte marimi fizice, ca de exemplu legea lui Gauss pentru
fluxul campului electric:
(egal prin definitie) este faptul ca intr-o singura relatie
se poate scrie atat definitia unei marimi, cat si legea care da dependenta
marimii respective de alte marimi fizice, ca de exemplu legea lui Gauss pentru
fluxul campului electric:
![]()
Legile si teoremele fizice se exprima in general prin formule, insa exista si legi ce se exprima prin fraze: de exemplu legea a treia a dinamicii, sau prima lege a frecarii (forta de frecare dintre doua corpuri nu depinde de marimea suprafetei de contact dintre acele corpuri).
1.7 Marimi fundamentale si marimi derivate
Unele marimi ca timpul sau spatiul nu pot fi definite in functie de alte marimi deja determinate, neexistand relatii de definitie pentru aceste doua marimi. Acest fapt se reflecta asupra faptului ca numarul de relatii principale dintre marimile fizice este mai mic decat numarul marimilor fizice. Asadar, pentru a determina toate marimile cunoscute este nevoie sa alegem un numar anume de marimi fundamentale, iar celelalte marimi pe care le numim derivate sa fie definite toate in functie de marimile fundamentale.
Marimile fundamentale se definesc in mod direct, prin indicarea procedeului de masurare si stabilirea unitatii de masura. Cu toate acestea, procedeul de masurare a unei marimi fundamentale nu este complet arbitrar, el trebuind sa satisfaca conditia generala ca raportul valorilor a doua marimi fundamentale de aceeasi natura sa fie independent de unitatea de masura folosita (acest raport trebuie sa ramana constant cand se schimba unitatea de masura). Definitia lungimii ar fi marimea care se masoara punand cap la cap unitatea de lungime astfel incat numarul de suprapuneri ale lungimii unitate peste lungimea de masurat sa fie minim. Unitatea de lungime se alege in functie de o anumita lungime care se gaseste in natura, sau o lungime construita de om in anumite conditii si pastrata cu anumite precautii.
Unitatile de masura pentru marimile fundamentale pot fi alese arbitrar, independent unele fata de altele. Pentru marimile derivate insa unitatile nu pot fi alese independent, ele depinzand de cele ale marimilor fundamentale la fel cum depinde marimea derivata fata de marimile fundamentale. Din aceasta relatie de dependenta se obtine si procedeul de masurare.
Marimile fundamentale din fizica se introduc intr-o anumita ordine, prin legi in care apar doua marimi noi fata de celelalte marimi determinate in alte capitole ale fizicii. Primul capitol este considerat geometria, ale carei postulate sunt legi experimentale in fizica, si in care este nevoie de o singura marime fundamentala, lungimea. Prima relatie din cinematica, care defineste viteza:
![]()
introduce doua marimi noi, viteza si timpul. Alegand timpul drept marime
fundamentala putem determina viteza, astfel ca in cinematica este nevoie de
doua marimi fundamentale: lungimea ![]() si timpul
si timpul ![]() .
.
In dinamica, pe langa lungime si timp mai este
nevoie de o marime fundamentala, care poate fi masa ![]() sau forta
sau forta ![]() de regula se alege
masa.
de regula se alege
masa.
In electricitate si fotometrie sunt necesare patru
marimi fundamentale, primele trei fiind ![]() ,
, ![]() si
si ![]() , cea de-a patra fiind respectiv intensitatea curentului
electric
, cea de-a patra fiind respectiv intensitatea curentului
electric ![]() , respectiv intensitatea luminoasa
, respectiv intensitatea luminoasa ![]() . In termodinamica si caldura sunt necesare cinci marimi
fundamentale:
. In termodinamica si caldura sunt necesare cinci marimi
fundamentale: ![]() ,
, ![]() si
si ![]() , a patra si a cincea fiind temperatura
, a patra si a cincea fiind temperatura ![]() , respectiv cantitatea de substanta
, respectiv cantitatea de substanta ![]() .
.
Numarul unitatilor
fundamentale fiecare din capitol al fizicii este arbitrar, acesta fiind mai
mare sau mai mic in functie de numarul constantelor cu dimensiuni (constante
universale). De exemplu, daca in electricitate s-ar scrie relatia dintre
intensitatea curentului electric si variatia sarcinii electrice in timp prin
introducerea unei constante cu dimensiuni ![]() :
:
![]() ,
,
atunci electromagnetismul ar avea nevoie de cinci marimi fundamentale, deoarece ar trebui aleasa, pe langa marimile fundamentale deja mentionate, si sarcina electrica (sistemul Gauss).
Numarul marimilor fundamentale poate fi redus prin
anumite relatii de legatura intre lungime si timp care contin o constanta
universala, ca de exemplu ![]() , unde
, unde ![]() este viteza luminii in
vid. Luand viteza luminii egala cu unitatea, se poate determina timpul in
functie de lungime si astfel timpul devine o marime derivata, cu unitatea
definita ca timpul in care lumina parcurge unitatea de lungime in vid. In
aceasta situatie marimile dinamicii s-ar putea determina cu ajutorul unei
singure marimi fundamentale, lungimea. Insa din punct de vedere practic aceste
sisteme cu un numar redus de marimi fundamentale nu sunt utile.
este viteza luminii in
vid. Luand viteza luminii egala cu unitatea, se poate determina timpul in
functie de lungime si astfel timpul devine o marime derivata, cu unitatea
definita ca timpul in care lumina parcurge unitatea de lungime in vid. In
aceasta situatie marimile dinamicii s-ar putea determina cu ajutorul unei
singure marimi fundamentale, lungimea. Insa din punct de vedere practic aceste
sisteme cu un numar redus de marimi fundamentale nu sunt utile.
Pe langa notiunile de marime fundamentala si derivata se mai utilizeaza, atunci cand relatiile fizice sunt scrise sub o forma foarte generala, cu mai multe constante fizice, termenii de marime primitiva si marime secundara. Constantele fizice fiind si ele marimi fizice, numarul marimilor devine mult mai mare decat numarul relatiilor dintre ele, in consecinta ar trebui ales un numar mai mare de marimi care se definesc direct. Aceste marimi se mai numesc si marimi primitive, si se definesc in mod direct prin indicarea procedeului de masura si stabilirea unitatii de masura. Marimile secundare se definesc cu ajutorul marimilor primitive. In final, o parte dintre marimile primitive (in general cele pentru care se pot realiza etaloane) se aleg drept marimi fundamentale, celelalte marimi primitive si marimile secundare devenind marimi derivate, care se definesc numai in functie de marimile fundamentale.
1.8 Calculul cu marimi si calculul cu valori
Plecand de la relatia ce
defineste marimea fizica ![]() drept produsul
simbolic intre valoarea
drept produsul
simbolic intre valoarea ![]() si unitatea de masura
si unitatea de masura ![]()
![]() , (1.1)
, (1.1)
putem efectua pentru deducerea teoremelor din fizica operatii direct cu marimi, fie cu valorile acestora. Pentru a face deosebirea intre calculul cu marimi si cel cu valori, precizam cateva reguli privind principalele operatii utilizate.
Egalitatea se poate defini numai pentru marimi de aceeasi natura. De exemplu, din cauza naturii lor diferite, densitatea relativa a unui mediu nu poate fi egala cu permitivitatea sau cu permeabilitatea relativa, chiar daca aceste marimi adimensionale ar avea aceeasi valoare. Pentru fiecare tip de marimi stabilirea egalitatii cere cel putin un procedeu particular. Intr-un fel sunt egali doi curenti, in alt fel sunt egale doua densitati sau doua lungimi.
Adunarea se defineste de asemenea numai intre doua marimi de aceeasi natura. Acestea pot fi adunate daca in definitia lor nu intervine o constanta aditiva arbitrara (alegerea arbitrara a unei origini), asa cum se intampla cu temperatura fata de o temperatura de origine, potentialul electric fata de Pamant (considerat ca un conductor de potential nul) etc.. Nu are sens fizic adunarea marimilor de natura diferita, ca de exemplu energia cu momentul fortei, chiar daca acestea prezinta acelesi dimensiuni.
Suma a doua marimi fizice de aceeasi natura se defineste prin relatia:
![]() (1.2)
(1.2)
Adunarea valorilor a doua marimi de aceeasi natura
are insa un caracter mai restrictiv, astfel ca se pot aduna numai valori care reprezinta
rezultatul unor masuratori facute cu aceeasi unitate. De exemplu, prin adunarea lungimilor ![]() si
si ![]() obtinem lungimea
obtinem lungimea ![]() :
:
![]()
Folosind relatia dintre unitatea de lungime si submultiplii acesteia s-a obtinut pentru lungimea suma forma obisnuita, ca produs intre valoare si unitate:
![]()
Adunand valorile celor doua lungimi s-ar obtine ![]() ceea ce nu are sens fizic.
ceea ce nu are sens fizic.
Daca marimile ce reprezinta cei doi termeni ai
sumei sunt exprimate in aceeasi unitate de masura, de exemplu ![]() , atunci se poate da factor comun aceasta unitate in formula
(1.2):
, atunci se poate da factor comun aceasta unitate in formula
(1.2):
![]() . (1.3)
. (1.3)
Daca intamplator valorile a doua marimi ce se aduna sunt egale, aceasta valoare nu poate fi data ca factor comun decat in cazul cand marimile sunt exprimate in aceeasi unitate de masura.
Ridicarea la putere a unei marimi se face la
fel ca ridicarea la putere a unui produs obisnuit, cu precizarea ca puterea
factorului simbolic unitate
constituie o unitate derivata. De
exemplu, ridicand la puterea a treia o lungime ![]() , obtinem:
, obtinem:
![]() ,
,
unde metrul cub reprezinta o unitate derivata.
Inmultirea mai multor
marimi reprezinta
produsul acelor marimi, dupa regulile inmultirii obisnuite in algebra. Factorul
simbolic al produsului, care se obtine prin inmultirea factorilor simbolici ai
fiecarei marimi, reprezinta o unitate derivata. Inmultind de exemplu forta ![]() cu distanta
cu distanta ![]() , obtinem lucrul mecanic (energia)
, obtinem lucrul mecanic (energia) ![]() :
:
![]()
Astfel, energia are valoarea de 50, iar factorul ![]() reprezinta o unitate derivata. Atat marimile cat si unitatile
vor fi tratate ca factori algebrici. Din exemplul de mai sus se poate observa
ca o relatie care exprima produsul a doua marimi se poate desface in cazul
general intr-o relatie de valori si o alta intre unitati:
reprezinta o unitate derivata. Atat marimile cat si unitatile
vor fi tratate ca factori algebrici. Din exemplul de mai sus se poate observa
ca o relatie care exprima produsul a doua marimi se poate desface in cazul
general intr-o relatie de valori si o alta intre unitati:
![]() ,
(1.4)
,
(1.4)
cu ![]() ,
, ![]() ,
, ![]() , sau
, sau ![]() ,
, ![]() ,
, ![]() .
.
Astfel, relatia (1.4) se desface in relatiile
![]() si
si ![]() (1.5)
(1.5)
Singurele dificultati la desfacerea unei relatii intre marimi in doua relatii, una intre valori si alta intre unitati, apar cand relatia dintre marimi contine un coeficient numeric. De obicei acest coeficient numeric trece in relatia dintre valori, relatia dintre unitati ramanand fara coeficient numeric. In acest caz unitatile formate sunt coerente, nefiind legate prin coeficienti numerici. De exemplu formula ariei unui cerc, care se scrie ca relatie intre marimi:
![]()
se desface de obicei sub forma ![]() si
si ![]() .
.
In unele cazuri insa se foloseste coeficientul numeric ![]() in relatia dintre
unitati:
in relatia dintre
unitati:
![]() ;
;![]() ,
,
Astfel, noua unitate de arie va fi metrul circular:
![]() ,
,
definit ca aria unui cerc a carui raza este de un metru. Se poate observa usor ca metrul circular este o marime necoerenta.
1.9 Formule fizice. Coeficientul parazit
Asa cum s-a aratat, oricarei entitati (marimi)
fizice ![]() i se asociaza o
valoare numerica
i se asociaza o
valoare numerica ![]() si o unitate de masura
si o unitate de masura
![]() , astfel ca:
, astfel ca:
![]() ,
,
unde![]() este un numar adimensional
fiind raportul a doua marimi de aceeasi natura. Daca se masoara marimea
este un numar adimensional
fiind raportul a doua marimi de aceeasi natura. Daca se masoara marimea ![]() cu unitati diferite,
se obtin valori diferite:
cu unitati diferite,
se obtin valori diferite:
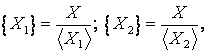
de unde
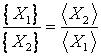 (1.6)
(1.6)
Relatia (1.6) constituie o teorema fundamentala a unitatilor de masura si stabileste ca raportul valorilor numerice ale unor entitati fizice este egal cu inversul raportului unitatilor de masura.
Intre o formula fizica si o formula matematica exista unele deosebiri. Formulele fizice cuprind marimi masurabile pentru care trebuie indicate valorile, cat si unitatile de masura, in timp ce in formulele matematice intra numai simbolurile marimilor respective. Sa luam drept un exemplu formula volumului, care din punct de vedere matematic se scrie:
![]() (1.7)
(1.7)
Din punct de vedere fizic insa formula (1.7) trebuie scrisa astfel:
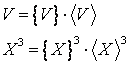
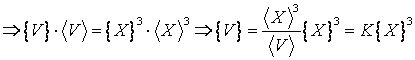 ,
,
unde
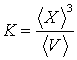 (1.8)
(1.8)
se numeste coeficient parazit al formulei fizice, iar valoarea sa depinde
de unitatile de masura ale marimilor care intra in formula (1.7). De exemplu, daca
![]() si
si ![]()
![]()
![]() .
.
Daca volumul se masoara in ![]() ,
, ![]() , si se spune ca s-a lucrat intr-un sistem coerent de unitati de masura. Eliminarea coeficientului
parazit conduce la o conditionare a unitatilor de masura pentru unitatile marimilor
derivate, pentru care trebuie alese numai acele unitati care rezulta din
unitatile marimilor fundamentale. Cand
, si se spune ca s-a lucrat intr-un sistem coerent de unitati de masura. Eliminarea coeficientului
parazit conduce la o conditionare a unitatilor de masura pentru unitatile marimilor
derivate, pentru care trebuie alese numai acele unitati care rezulta din
unitatile marimilor fundamentale. Cand ![]() (relatia de conditionare
pentru unitatea de volum), relatia fizica se va scrie
(relatia de conditionare
pentru unitatea de volum), relatia fizica se va scrie ![]() si coincide cu relatia
matematica
si coincide cu relatia
matematica ![]() .
.
Prezenta coeficientului parazit in formulele fizice conduce la complicarea formei acestora. Pentru eliminarea coeficientului parazit era nevoie de un sistem coerent de unitati de masura, care sa contina un numar restrans de unitati fundamentale, ca si unitati derivate care sa rezulte din unitatile fundamentale.
1.10 Ecuatii intre marimi si ecuatii intre valori numerice
In stiinta si in tehnica se utilizeaza doua tipuri de ecuatii:
- ecuatii intre marimi, in care marimea fizica (produsul intre valoarea numerica si unitate) este indicata printr-un simbol literal. Aceste ecuatii au avantajul ca sunt independente de alegerea unitatilor de masura;
- ecuatii intre valori numerice, unde valorile numerice ale marimilor fizice depind de alegerea unitatilor de masura pentru marimile corespunzatoare.
Sa consideram ecuatia vitezei in miscarea rectilinie si uniforma:
![]()
Daca folosim drept unitati de masura metrul pentru lungime, secunda pentru timp si metrul pe secunda pentru viteza, obtinem ecuatia intre valorile numerice:
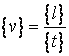
Daca insa folosim drept unitati de masura metrul pentru lungime, secunda
pentru timp si kilometrul pe ora pentru viteza, tinand cont ca ![]() si
si ![]() , atunci
, atunci ![]() , si obtinem ecuatia intre valorile numerice:
, si obtinem ecuatia intre valorile numerice:
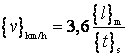
Este evident ca alegand alte unitati de masura vom obtine in loc de numarul 3,6 alt numar. Daca nu se precizeaza unitatile de masura intr-o ecuatie intre valori numerice, atunci ecuatia nu poate fi utilizata sub aceasta forma.
1.11 Dimensiunile marimilor. Sisteme de dimensiuni
S-a aratat ca procedeul de masurare a marimilor fundamentale nu este arbitrar, conditia generala impusa fiind ca raportul valorilor a doua marimi fundamentale de aceeasi natura sa fie independent de unitatea aleasa. Aceasta conditie generala se impune si la definitia sau determinarea marimilor derivate. Pentru ca raportul dintre valorile a doua marimi derivate de aceeasi natura sa fie independent de unitatea aleasa, relatiile prin care se definesc sau se determina marimile derivate in functie de marimile fundamentale nu sunt arbitrare.
S-a aratat de asemenea ca raportul valorilor unei aceleasi marimi se modifica cu schimbarea unitatilor, fiind egal cu inversul raportului dintre unitati.
Problema esentiala este de a determina in ce
conditii se respecta cerinta principala si generala referitoare la independenta
de unitatile de masura a raportului dintre valorile a doua marimi de aceeasi
natura. In acest scop vom considera doua marimi derivate de aceeasi natura notate
cu ![]() si
si ![]() , masurate fiecare cu doua unitati de masura,
, masurate fiecare cu doua unitati de masura, ![]() si
si ![]() :
:
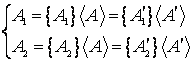 (1.9)
(1.9)
Vom stabili forma functiei prin care valoarea marimii derivate depinde de
valorile marimilor fundamentale (sa presupunem lungimea, timpul si masa in
demonstratia ce urmeaza), astfel incat raportul valorilor celor doua marimi ![]() , respectiv
, respectiv ![]() , sa fie independent de unitatea aleasa, adica sa fie
independent de unitatile alese pentru masurarea marimilor fundamentale. In
acest scop, presupunem pentru functie o forma de tipul:
, sa fie independent de unitatea aleasa, adica sa fie
independent de unitatile alese pentru masurarea marimilor fundamentale. In
acest scop, presupunem pentru functie o forma de tipul:
![]() , (1.10)
, (1.10)
care indica expresia valorii ![]() a marimii derivate
fata de unitatea
a marimii derivate
fata de unitatea ![]() in functie de valorile
in functie de valorile
![]() si
si ![]() ale lungimii-tip,
timpului-tip si respectiv masei-tip in anumite unitati, si functia:
ale lungimii-tip,
timpului-tip si respectiv masei-tip in anumite unitati, si functia:
![]() , (1.11)
, (1.11)
indicand expresia valorii ![]() a marimii derivate
fata de unitatea
a marimii derivate
fata de unitatea ![]() in functie de valorile
in functie de valorile
![]() si
si ![]() ale lungimii-tip, timpului-tip si respectiv masei-tip in
unitatile al caror sistem contine si unitatea
ale lungimii-tip, timpului-tip si respectiv masei-tip in
unitatile al caror sistem contine si unitatea ![]() .
.
Conditia generala cere ca raportul
valorilor marimilor derivate ![]() si
si ![]() sa nu depinda de
unitatile alese, conform relatiilor (1.9):
sa nu depinda de
unitatile alese, conform relatiilor (1.9):
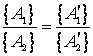 (1.12)
(1.12)
Tinand cont de relatiile (1.10) si (1.11), relatia (1.12) devine:
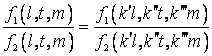 (1.13)
(1.13)
Egalitatea din expresia (1.13) este indeplinita daca functia din membrul al
doilea nu depinde de ![]() si
si ![]() ceea ce este posibil numai daca functia
ceea ce este posibil numai daca functia ![]() este de forma
produsului unor puteri:
este de forma
produsului unor puteri:
![]() , (1.14)
, (1.14)
unde ![]() si
si ![]() sunt numere arbitrare
intregi sau fractionare care pot avea valori pozitive, nule sau negative.
Factorul
sunt numere arbitrare
intregi sau fractionare care pot avea valori pozitive, nule sau negative.
Factorul ![]() este o constanta care
nu depinde de unitatile marimilor fundamentale. Produsele si puterile pot
reprezenta oricare dintre produsele sau puterile definite in calculul cu aceste
marimi. Numai pentru aceasta forma a functiei
este o constanta care
nu depinde de unitatile marimilor fundamentale. Produsele si puterile pot
reprezenta oricare dintre produsele sau puterile definite in calculul cu aceste
marimi. Numai pentru aceasta forma a functiei ![]() se poate simplifica
produsul
se poate simplifica
produsul ![]() intre numarator si
numitor. In acest caz, raportul dintre valorile celor doua marimi derivate
intre numarator si
numitor. In acest caz, raportul dintre valorile celor doua marimi derivate ![]() si
si ![]() nu depinde de unitatea
aleasa de masura pentru aceste marimi. Deoarece unitatea marimii derivate
depinde de unitatile marimilor fundamentale, rezulta ca acest raport ramane
constant chiar daca se schimba independent unitatile marimilor fundamentale.
Plecand de la aceste consideratii se ajunge la introducerea notiunii de dimensiune.
nu depinde de unitatea
aleasa de masura pentru aceste marimi. Deoarece unitatea marimii derivate
depinde de unitatile marimilor fundamentale, rezulta ca acest raport ramane
constant chiar daca se schimba independent unitatile marimilor fundamentale.
Plecand de la aceste consideratii se ajunge la introducerea notiunii de dimensiune.
Pornind de la formula (1.14)
se poate scrie expresia raportului a doua valori ale marimii ![]() fata de unitatile
fata de unitatile ![]() si
si ![]() :
:

Chiar in cazul schimbarii unitatilor fundamentale, raportul ![]() a doua valori ale
aceleasi marimi derivate este egal cu produsul rapoartelor
a doua valori ale
aceleasi marimi derivate este egal cu produsul rapoartelor
![]()
la puterile ![]() si
si ![]() :
:
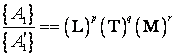 (1.15)
(1.15)
(valorile marimilor fundamentale in cele doua sisteme de unitati din care
fac parte respectiv unitatile![]() si
si![]() ). Produsul (1.15) se numeste si dimensiunea (sau ecuatia
dimensionala) marimii derivate
). Produsul (1.15) se numeste si dimensiunea (sau ecuatia
dimensionala) marimii derivate![]() , si se noteaza simbolic
, si se noteaza simbolic
![]() (1.16)
(1.16)
Relatia (1.16) se poate citi astfel: Marimea ![]() are dimensiunea
are dimensiunea ![]() in raport cu lungimea,
in raport cu lungimea,
![]() in raport cu timpul si
in raport cu timpul si
![]() in raport cu masa. In
cazul
in raport cu masa. In
cazul ![]() :
:
![]()
prin urmare marimea respectiva este o marime numerica, fara dimensiuni. Nedepinzand
de marimile fundamentale, nici unitatea sa nu va depinde de unitatile
fundamentale. De obicei unitatea marimilor fara dimensiuni se ia numarul
unitate. Ecuatia dimensionala pentru
o marime derivata presupune de fapt cunoasterea valorii coeficientilor![]() si
si![]() , iar pentru a o obtine se expliciteaza relatia de definitie
pana in membrul al doilea apar numai marimi fundamentale. De exemplu, puterea
, iar pentru a o obtine se expliciteaza relatia de definitie
pana in membrul al doilea apar numai marimi fundamentale. De exemplu, puterea ![]() se defineste astfel:
se defineste astfel:
![]() ,
,
iar ecuatia dimensionala este:
![]()
Teoremele folosite pentru stabilirea dimensiunilor marimilor derivate sunt urmatoarele:
1. Dimensiunile unei marimi ![]() egala cu produsul a
doua marimi
egala cu produsul a
doua marimi ![]() si
si ![]() sunt egale cu produsul
dimensiunilor celor doua marimi:
sunt egale cu produsul
dimensiunilor celor doua marimi:
![]()
Daca ![]() si
si ![]() , atunci
, atunci ![]() .
.
2. Dimensiunile unei marimi ![]() egala cu raportul
marimilor
egala cu raportul
marimilor ![]() si
si ![]() sunt egale cu raportul
dimensiunilor celor doua marimi:
sunt egale cu raportul
dimensiunilor celor doua marimi:
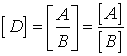 ,
,
sau ![]()
3. Dimensiunile unei marimi ![]() egala cu marimea
egala cu marimea ![]() ridicata la puterea
ridicata la puterea ![]() sunt egale cu puterea
a
sunt egale cu puterea
a ![]() -a a dimensiunilor marimii
-a a dimensiunilor marimii ![]() :
:
![]() ,
,
sau ![]()
Prima teorema se demonstreaza scriind fiecare marime ca produsul intre valoare si unitate, presupunand ca fiecare marime se masoara cu doua unitati:

Relatia care exprima marimea ![]() se poate scrie sub doua
forme,
se poate scrie sub doua
forme, ![]() sau
sau ![]() ; impartind membru cu membru obtinem:
; impartind membru cu membru obtinem:
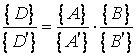
Tinand cont de relatia (1.15) si de relatia corespunzatoare pentru marimea ![]() :
:
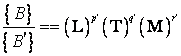 (1.17)
(1.17)
obtinem
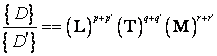 ,
,
adica relatia
![]()
In acelasi mod se demonstreaza, fara dificultate, celelalte teoreme.
Importanta ecuatiilor de dimensiuni consta in urmatoarele:
- permit verificarea omogenitatii formulelor fizice;
- cu aceste ecuatii se pot stabili ecuatiile unitatilor;
- intervin in problemele de schimbare a unitatilor.
Un sistem de dimensiuni se caracterizeaza prin grupul marimilor fundamentale din care se pot determina univoc toate celelalte marimi fizice. Desi sistemul de dimensiuni din fiecare capitol al fizicii este complet arbitrar in privinta naturii si numarului marimilor fundamentale, se pun doua conditii:
- formulele fizicii sa fie scrise cu un numar cat mai mic de constante universale, ceea ce ar conduce la un numar minim de marimi fundamentale;
- sa existe cat mai putine posibil marimi cu aceleasi dimensiuni, fapt ce ar conduce la un numar cat mai mare de marimi fundamentale.
Pentru sistemul ales in prezent, desi exista marimi cu aceeasi dimensiuni, numarul acestora este foarte mic. In mecanica de exemplu, dimensiunile momentului fortei coincid cu ale energiei, si ale viscozitatii cinematice cu ale modulului de difuzie. In electricitate coincid dimensiunile fluxului inductiei electrice cu ale sarcinii electrice, si ale inductiei electrice cu ale densitatii superficiale de sarcina electrica. Aceste egalitati dimensionale ridica insa problema daca marimile respective sunt sau nu de aceeasi natura.
Doua sisteme de dimensiuni pot diferi atat prin numarul marimilor fundamentale, cat si prin natura acestora. Din punctul de vedere al naturii marimilor fundamentale, se aleg acele marimi pentru care realizarea de etaloane, in scopul concretizarii unitatii fundamentale, este mai usoara (de exemplu, se prefera masa in locul fortei sau impulsului). Din punctul de vedere al dimensiunilor se alege acel sistem de dimensiuni in care ecuatiile de dimensiuni au forma cea mai simpla (exponentii marimilor fundamentale din ecuatia dimensiunilor sa fie cat mai mici, de exemplu egali cu 1 sau cel mult cu 2).
1.12 Marimi de aceeasi natura si marimi de natura diferita
Dupa cum s-a aratat, numarul
marimilor cu aceleasi dimensiuni dintr-un sistem de dimensiuni este cu atat mai
mare cu cat numarul marimilor fundamentale este mai mic. Doua marimi cu
aceleasi dimensiuni intr-un sistem de dimensiuni pot avea dimensiuni diferite in
alt sistem de dimensiuni. De exemplu, in sistemul ![]() modulul de difuzie si
viscozitatea cinematica au aceleasi dimensiuni
modulul de difuzie si
viscozitatea cinematica au aceleasi dimensiuni ![]() . In sistemul de dimensiuni
. In sistemul de dimensiuni ![]() modulul de difuzie are
dimensiunile
modulul de difuzie are
dimensiunile ![]() , iar viscozitatea cinematica
, iar viscozitatea cinematica ![]() . Intrucat in sisteme
diferite de dimensiuni exista marimi diferite care au aceleasi dimensiuni, apare
firesc intrebarea daca marimile cu aceleasi dimensiuni sunt in realitate de
aceeasi natura, sau se poate intampla ca marimi cu aceleasi dimensiuni sa fie
de natura diferita?
. Intrucat in sisteme
diferite de dimensiuni exista marimi diferite care au aceleasi dimensiuni, apare
firesc intrebarea daca marimile cu aceleasi dimensiuni sunt in realitate de
aceeasi natura, sau se poate intampla ca marimi cu aceleasi dimensiuni sa fie
de natura diferita?
Asa cum s-a aratat, in procesul masurarii comparam o marime cu o alta marime de aceeasi natura numita unitate. Evident ca toate marimile de aceeasi natura se vor masuara cu aceeasi unitate si in acelasi mod, adica folosind acelasi procedeu de masurare. Astfel, trebuie sa adaugam la conditia ca doua marimi sa fie de aceeasi natura si pe aceea referitoare la masurarea cu acelasi procedeu.
Lucrul mecanic si momentul unei forte sunt un
exemplu de marimi cu aceleasi dimensiuni (in sistemele ![]() si
si ![]() ), insa de natura diferita. Procedeele de masura fiind
diferite, cele doua marimi se vor masura cu unitati diferite. Un alt exemplu
este cazul marimilor fara dimensiuni (numerele pure, unghiul plan, unghiul solid,
panta, concentratia procentuala, densitatea relativa etc.). Aceste marimi sunt
de natura diferita, deoarece fiecare dintre ele are un anumit procedeu de
masurare, iar aceste procedee sunt diferite cand trecem de la o marime la alta.
In consecinta, unitatile pentru aceste marimi vor fi diferite: pentru numerele
pure unitatea va fi cifra unu (simbol 1), pentru unghiul plan - radianul,
pentru unghiul solid - steradianul, pentru panta - procentul s.a.m.d.
), insa de natura diferita. Procedeele de masura fiind
diferite, cele doua marimi se vor masura cu unitati diferite. Un alt exemplu
este cazul marimilor fara dimensiuni (numerele pure, unghiul plan, unghiul solid,
panta, concentratia procentuala, densitatea relativa etc.). Aceste marimi sunt
de natura diferita, deoarece fiecare dintre ele are un anumit procedeu de
masurare, iar aceste procedee sunt diferite cand trecem de la o marime la alta.
In consecinta, unitatile pentru aceste marimi vor fi diferite: pentru numerele
pure unitatea va fi cifra unu (simbol 1), pentru unghiul plan - radianul,
pentru unghiul solid - steradianul, pentru panta - procentul s.a.m.d.
O alta problema importanta la stabilirea unitatilor de masura este daca din relatiile fizice se pot delimita sau nu marimile de aceeasi natura. Acest lucru este important la stabilirea unitatilor, deoarece pentru doua marimi de aceeasi natura se foloseste aceeasi unitate de masura. Marimile de aceeasi natura pot fi legate prin anumite relatii de egalitate, ca de exemplu teorema energiei cinetice:
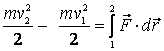
Marimile din aceasta formula (energia cinetica si lucrul mecanic) au acelasi procedeu de masurare, deci sunt de aceeasi natura si se masoara cu aceeasi unitate de masura. Insa intre marimi de natura diferita, desi cu aceleasi dimensiuni (lucrul mecanic si momentul fortei) nu exista o relatie de egalitate.
1.13 Omogenitatea relatiilor fizice
Relatiile fizice din orice capitol al fizicii trebuie sa fie valabile independent de sistemul de unitati adoptat. Asadar, schimbarea unitatilor de masura nu trebuie sa modifice egalitatea dintre cei doi membri ai unei relatii. Aceasta presupune ca toti membri care intra intr-o relatie fizica sa fie de aceeasi natura. In calculul dimensional acest fapt se rezuma la urmatoarea afirmatie: o anumita relatie este omogena daca toti termenii sai au aceleasi dimensiuni (si deci aceeasi natura). De exemplu, in teorema variatiei impulsului:
![]()
se poate observa usor ca fiecare termen are dimensiunile ![]() .
.
Derivata 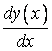 are aceleasi
dimensiuni cu raportul cresterilor finite
are aceleasi
dimensiuni cu raportul cresterilor finite ![]() , dupa cum si integrala
, dupa cum si integrala ![]() are aceleasi
dimensiuni cu produsul
are aceleasi
dimensiuni cu produsul ![]() .
.
Daca doua marimi sunt identice:
![]() ,
,
conditia de omogenitate a formulelor fizice
impune ca ![]() si
si ![]() sa aiba aceleasi
dimensiuni. Daca
sa aiba aceleasi
dimensiuni. Daca ![]() si
si ![]() , in relatia dimensionala:
, in relatia dimensionala:
![]()
trebuie indeplinite conditiile:
![]()
Numai in acest caz legile fizicii raman invariante fata de schimbarea unitatilor de masura ale marimilor fizice fundamentale.
Tinand seama de conditia de omogenitate a formulelor fizice, se poate verifica daca o formula fizica este corecta, sau se pot stabili anumite formule fizice daca stim de cine depinde marimea pentru care stabilim formula respectiva.
Exemplul 1
Sa presupunem ca formula perioadei ![]() a unui pendul
matematic ar fi:
a unui pendul
matematic ar fi:
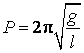
![]()
Ecuatia dimensionala este in acest caz
![]()
Dimensiunile marimilor care apar in formula sunt:
![]() ;
; ![]() ;
; ![]() .
.
Din relatiile de mai sus obtinem:
![]()
ceea ce este imposibil, de unde rezulta ca formula perioadei este incorecta.
Stabilirea formulei corecte se face prin analiza
dimensionala cunoscand ca perioada pendulului depinde de lungimea sa ![]() si de acceleratia
gravitationala
si de acceleratia
gravitationala ![]() :
:
![]() ,
,
Ecuatia dimensionala a perioadei va fi:
![]() ,
,
Din conditia de omogenitate obtinem sistemul de ecuatii si solutia acestuia:
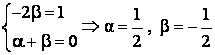 ,
,
astfel formula fizica se va scrie, pana la un factor adimensional:
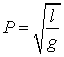
Valoarea
factorului adimensional se stabileste, in general, pe baza unor calcule
teoretice si in cazul de fata are valoarea ![]() , astfel ca formula riguroasa este
, astfel ca formula riguroasa este
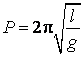 .
.
1.14 Constante fizice
Constantele fizice sunt de doua feluri:
- constante de material (tensiunea superficiala, modulul lui Young, caldura specifca etc.)
- constante universale (viteza luminii in vid, constanta gazelor ideale, constanta gravitationala, constanta structurii fine, constanta lui Planck, anumite constante numerice etc.).
Constantele universale sunt
de doua categorii: constante numerice
sau coeficienti numerici (de exemplu ![]() care apare in formula
perioadei pendulului) si constante
dimensionale, a caror valoare depinde de unitatile alese pentru masurarea
marimilor respective (constanta atractiei universale
care apare in formula
perioadei pendulului) si constante
dimensionale, a caror valoare depinde de unitatile alese pentru masurarea
marimilor respective (constanta atractiei universale ![]() ). Trebuie precizat ca daca intr-o formula se
introduce valoarea unei constante universale cu dimensiuni, formula nu mai
poate fi interpretata ca o relatie intre marimi, ci ca o relatie intre valori,
si in acest caz trebuie indicate intre paranteze unitatile folosite.
). Trebuie precizat ca daca intr-o formula se
introduce valoarea unei constante universale cu dimensiuni, formula nu mai
poate fi interpretata ca o relatie intre marimi, ci ca o relatie intre valori,
si in acest caz trebuie indicate intre paranteze unitatile folosite.
1.15 Dimensiunea unei marimi fizice
Orice marime fizica ![]() se poate exprima in
functie de alte marimi printr-o ecuatie. Aceasta expresie poate sa contina o suma de termeni, fiecare
dintre acesti termeni fiind exprimat prin produsul puterilor marimilor
fundamentale
se poate exprima in
functie de alte marimi printr-o ecuatie. Aceasta expresie poate sa contina o suma de termeni, fiecare
dintre acesti termeni fiind exprimat prin produsul puterilor marimilor
fundamentale![]() care apartin unui set ales. Uneori acest produs este
multiplicat cu un factor numeric, avand forma
care apartin unui set ales. Uneori acest produs este
multiplicat cu un factor numeric, avand forma ![]() , unde ansamblul exponentilor
, unde ansamblul exponentilor ![]() este acelasi pentru
fiecare termen. Dimensiunea marimii
este acelasi pentru
fiecare termen. Dimensiunea marimii ![]() va fi astfel exprimata
prin produsul dimensiunilor
va fi astfel exprimata
prin produsul dimensiunilor
![]() ,
,
unde ![]() reprezinta
dimensiunile marimilor fundamentale
reprezinta
dimensiunile marimilor fundamentale ![]() , iar
, iar ![]() se numesc exponenti
dimensionali. O marime cu exponentii dimensionali egali cu zero se numeste marime fara dimensiune, produsul sau de
dimensiuni sau dimensiunea sa fiind 1, iar marimea se exprima printr-un numar.
se numesc exponenti
dimensionali. O marime cu exponentii dimensionali egali cu zero se numeste marime fara dimensiune, produsul sau de
dimensiuni sau dimensiunea sa fiind 1, iar marimea se exprima printr-un numar.
Exemplul 2.
Exprimand dimensiunile marimilor fundamentale lungime, masa, timp, temperatura termodinamica, cantitate de substanta, curent electric si intensitate luminoasa prin simbolurile indicate mai jos:
![]() ,
,
se pot exprima dimensiunile oricarei marimi fizice prin simbolurile respective si exponentii dimensionali corespunzatori unei anumite marimi (tabelul 1).
Tabelul 1. Dimensiunile unor marimi fizice
|
Marimea |
Dimensiunea |
Marimea |
Dimensiunea |
|
Viteza |
|
Rezistenta electrica |
|
|
Viteza unghiulara |
|
Inductanta |
|
|
Forta |
|
Permeabilitate |
|
|
Energie |
|
Capacitate electrica |
|
|
Potential electric |
|
Densitate relativa | |
|
Permitivitate |
|
Inductie magnetica |
|
|
Flux magnetic |
|
Capacitate calorica |
|
|
Iluminare |
|
Caldura specifica |
|
|
Constanta Faraday |
|
Randament energetic |
1.16 Analiza dimensionala a formulelor fizice
Dupa cum se stie, Sistemul International cuprinde in prezent 7 unitati fundamentale si doua unitati suplimentare. Intr-un sistem coerent, unitatile marimilor derivate trebuie sa se exprime numai prin unitati fundamentale sau suplimentare. Este clar ca o unitate derivata se poate exprima si prin mai putin de 7 unitati fundamentale, de exemplu in mecanica, unde marimile derivate se pot exprima prin numai trei marimi fundamentale: lungime, timp si masa.
Referitor la legea a doua a dinamicii, forma matematica a acesteia este:
![]()
Relatia dimensionala se va scrie:
![]() ,
,
unde ![]() si
si ![]() , astfel ca
, astfel ca
![]() .
.
![]() reprezinta legea fizica, iar
reprezinta legea fizica, iar ![]() reprezinta relatia dimensionala intre marimile fizice
corespunzatoare.
reprezinta relatia dimensionala intre marimile fizice
corespunzatoare.
Dupa cum s-a aratat in sectiunea 1.9, daca inlocuim marimile din formula fizica cu valorile acestor marimi, forma formulei ce exprima relatia intre marimi nu se schimba (indiferent de unitatile de masura folosite), numai daca se admite ca unitatile de masura pentru marimile derivate se pot scrie in functie de unitatile de masura ale marimilor fundamentale printr-o expresie de forma:
![]() .
.
Altfel spus, orice marime ![]() trebuie exprimata dimensional
sub forma unui monom algebric format din puteri ale simbolurilor marimilor
fundamentale, exponentul fiecarei puteri fiind egal cu indicele puterii la care
acea marime fundamentala intra in definitia marimii derivate (
trebuie exprimata dimensional
sub forma unui monom algebric format din puteri ale simbolurilor marimilor
fundamentale, exponentul fiecarei puteri fiind egal cu indicele puterii la care
acea marime fundamentala intra in definitia marimii derivate (![]() . se mai numesc si dimensiunile
marimii derivate in raport cu marimea fundamentala corespunzatoare:
. se mai numesc si dimensiunile
marimii derivate in raport cu marimea fundamentala corespunzatoare:![]() ). In exemplul 3 se arata cum se determina dimensiunile
pentru unele dintre aceste marimi.
). In exemplul 3 se arata cum se determina dimensiunile
pentru unele dintre aceste marimi.
Exemplul 3.
Sa
deducem formula vitezei luminii in vid cunoscand ca ea depinde de
permitivitatea electrica ![]() si de permeabilitatea
magnetica
si de permeabilitatea
magnetica ![]() a vidului.
a vidului.
![]()
Pentru a stabili dimensiunile marimilor ![]() si
si ![]() , se procedeaza astfel:
, se procedeaza astfel:
- din formula lucrului mecanic ![]() efectuat asupra unei
sarcini electrice
efectuat asupra unei
sarcini electrice ![]() care se deplaseaza sub
diferenta de potential
care se deplaseaza sub
diferenta de potential ![]() :
:
![]() ,
,
rezulta
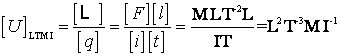 ,
,
de unde rezulta si unitatea pentru tensiune, voltul, exprimat in unitatile celor 4 marimi fundamentale folosite din sistemul SI:
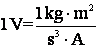 .
.
Din legea inductiei magnetice
![]()
rezulta
![]()
Din relatia de definitie a fluxului vectorului inductie a campului magnetic:
![]()
rezulta
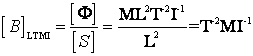
Din relatia de definitie a inductiei campului magnetic in vid:
![]()
rezulta
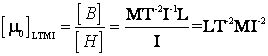
Din formula de definitie a capacitatii electrice ![]() :
:
![]()
rezulta
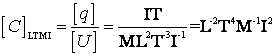 .
.
Din formula capacitatii unui condensator (de exemplu condensatorul plan):
![]()
rezulta
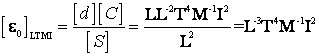
Ecuatia dimensionala a vitezei luminii va fi:
![]() .
.
Din conditia de omogenitate obtinem sistemul de ecuatii si solutia acestuia
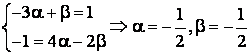
astfel formula fizica se va scrie, pana la un factor adimensional:
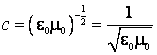
Se observa ca in aceasta formula factorul adimensional este egal cu unitatea.
Exemplul 4
Sa se adapteze relatia care
exprima lungimea de unda asociata unei particule elementare nerelativiste de masa
![]() , sarcina
, sarcina ![]() , accelerata la tensiunea
, accelerata la tensiunea ![]() , in functie de unitatile: nanometru (
, in functie de unitatile: nanometru (![]() ) pentru lungimea de unda; masa electronului (
) pentru lungimea de unda; masa electronului (![]() ) pentru masa
) pentru masa ![]() a particulei; sarcina
electronului (
a particulei; sarcina
electronului (![]() ) pentru sarcina
) pentru sarcina ![]() a particulei; voltul (
a particulei; voltul (![]() ) pentru tensiunea de accelerare
) pentru tensiunea de accelerare ![]() .
.
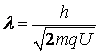 ,
,
unde![]() reprezinta constanta lui Planck. Relatia intre valori
corespunzatoare sistemului SI este:
reprezinta constanta lui Planck. Relatia intre valori
corespunzatoare sistemului SI este:
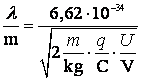
Transformand metrul in ![]() , kilogramul in mase electronice si coulombul in sarcini
electronice din relatiile cunoscute:
, kilogramul in mase electronice si coulombul in sarcini
electronice din relatiile cunoscute:
![]()
obtinem:
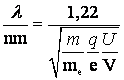 (1.18)
(1.18)
Din formula (1.18) rezulta ca pentru un electron accelerat la o tensiune de
1V, lungimea de unda asociata va avea valoarea ![]()
1.17 Unitati fundamentale si unitati derivate
Unitatile fundamentale se aleg pentru masurarea marimilor fundamentale, independent unele fata de altele, alegerea fiind conventionala.
Unitatile derivate sunt cele cu care se masoara marimile derivate. Aceste unitati nu sunt independente nici intre ele, nici fata de unitatile fundamentale. Regulile dupa care se formeaza unitatile derivate stabilesc mai multe aspecte care caracterizeaza o unitate derivata: ecuatia unitatii, denumirea, definitia si formula de transformare in alte unitati.
Plecand de la relatia de definitie a marimii derivate se stabilesc, in aceasta ordine:
a) ecuatia dimensiunilor marimii derivate din relatia prin care se determina aceasta marime;
b) ecuatia unitatii, prin inlocuirea marimilor fundamentale din ecuatia dimensiunilor cu unitatile fundamentale corespunzatoare. Pentru ca in ecuatia dimensiunilor nu apar coeficienti numerici, acestia nu vor apare nici in ecuatia unitatii;
c) denumirea unitatii se face cu ajutorul ecuatiei unitatii sau direct din relatia de definitie;
d) definitia, in care unitatea marimii respective se obtine in cazul in care toate celelalte marimi vor fi egale fiecare cu unitatea corespunzatoare fiecareia;
e) formula de transformare, care se obtine din ecuatia unitatii inlocuind unitatile fundamentale cu formulele lor de transformare.
Drept exemplu, sa stabilim
unitatea pentru energie din relatia ![]() , care contine coeficientul numeric
, care contine coeficientul numeric ![]() , avand numele special Joule si simbolul J.
, avand numele special Joule si simbolul J.
a)![]() b)
b) ![]() c)
c)![]() d)
d)![]() daca
daca ![]() si
si ![]() . Definitie: Joule-ul
este energia cinetica a unui corp cu masa de doua kilograme, care se deplaseaza
cu o viteza de un metru pe secunda.
. Definitie: Joule-ul
este energia cinetica a unui corp cu masa de doua kilograme, care se deplaseaza
cu o viteza de un metru pe secunda.
e) ![]() .
.
Unitatile derivate stabilite prin procedeul de mai sus se mai numesc coerente. Coerenta este dimensionala, deoarece la baza definitiei acestor unitati sta ecuatia dimensiunilor marimii. In consecinta, indiferent de relatiile care contin marimea respectiva (in cazul de sus energia) se obtine aceeasi ecuatie a unitatii marimii.
Doua unitati sunt identice numai
daca atat ecuatia unitatii, cat si definitia sunt aceleasi. De exemplu, desi au
aceeasi ecuatie, unitatea pentru momentul fortei si pentru lucrul mecanic nu au
aceeasi definitie. Desi marimile au aceleasi dimensiuni, ele sunt de natura
diferita, in consecinta unitatile celor doua marimi au denumiri diferite: ![]() Diferentierea
procedeelor de masurare atrage dupa sine diferentierea definitiilor unitatilor.
Diferentierea
procedeelor de masurare atrage dupa sine diferentierea definitiilor unitatilor.
1.18 Sisteme de unitati
Un sistem de unitati trebuie
sa posede un grup de unitati fundamentale. Unui sistem de dimensiuni ii pot
corespunde mai multe sisteme de unitati, ca de exemplu sistemului de dimensiuni
![]() ii corespund sistemele
de unitati
ii corespund sistemele
de unitati ![]() (metru-kilogram-secunda)
si
(metru-kilogram-secunda)
si ![]() (centimetru-gram-secunda).
(centimetru-gram-secunda).
Pentru folosirea practica a sistemelor de unitati
este nevoie ca unitatile fundamentale sa fie concretizate si pastrate in conditii
speciale, ceea ce se realizeaza sub forma etaloanelor.
Nu se realizeaza insa etaloane pentru unitatile fundamentale ale tuturor
sistemelor de unitati. Unitatile fundamentale ale altor sisteme de unitati
decat sistemul principal se definesc prin anumite relatii in functie de
unitatile sistemului principal. Ca exemplu prezentam cazul sistemului ![]() unde centimetrul si gramul difera de metru si kilogram. Nu se
realizeaza alt etalon pentru centimetru sau gram, ci se definesc in functie de
metru si kilogram astfel:
unde centimetrul si gramul difera de metru si kilogram. Nu se
realizeaza alt etalon pentru centimetru sau gram, ci se definesc in functie de
metru si kilogram astfel:
![]()
Un sistem de unitati trebuie sa indeplineasca anumite conditii:
- sa fie practic, adica la masurarea marimilor uzuale sa nu fie nevoie de valori foarte mari sau foarte mici;
- sa fie general, care sa se aplice in toate capitolele fizicii;
- sa fie coerent, in care unitatile derivate se formeaza dupa principiul coerentei dimensionale; intre aceste unitati nu exista coeficienti numerici;
- unitatile fundamentale sa fie independente intre ele din punct de vedere dimensional. Din acest punct de vedere chiar si Sistemul International are neajunsuri, deoarece in definitia amperului se foloseste metrul si kilogramul.
1.19 Etaloane si masuri
In paragraful 1.15 s-a aratat ca pentru folosirea unitatilor este nevoie de concretizarea acestora, prin relatiile de definitie sau de determinare a marimii, conform unor operatii precizate. Intrucat pentru marimile fundamentale concretizarea nu se poate obtine in acest mod, se folosesc asa numitele etaloane.
Etaloanele trebuie sa satisfaca o serie de cerinte, printre care:
- sa poata fi reconstituite in orice moment;
- sa prezinte variatii minime fata de influenta factorilor externi (presiune, temperatura, umiditate etc;
- materialele din care sunt confectionate sa nu sufere modificari de structura fizico-chimica in timp;
- sa fie usor de folosit in tehnica de masurare.
Trebuie precizat ca nu este nevoie ca pentru toate unitatile fundamentale din diferite sisteme de unitati sa existe cate un etalon. Cu toate acestea, numarul etaloanelor este egal cu numarul unitatilor fundamentale.
Metrologia se ocupa cu realizarea si conservarea etaloanelor. Etaloanele sunt de mai multe ordine: prototip, etalon de primul ordin, de ordinul doi, de ordinul trei etc. Etaloanele prototip de lungime si masa (metrul si kilogramul) sunt depozitate in camerele speciale ale pavilionului Breteuil de la Sèvres -Franta. Cu acestea sunt inchise etaloane de prim ordin. Dupa acestea se realizeaza copii, care constituie etaloane de ordinul doi, care se distribuie diferitelor tari. In aceste tari se construiesc etaloane de ordinul trei, folosite de institutele meteorologice si institutele de cercetari. Dupa aceste etaloane de ordinul trei se realizeaza masurile, care sunt folosite in practica zilnica. Exista masuri de lungime - rigle, rulete, de mase - cutia cu greutati, ca si masuri ale unor unitati derivate - de exemplu masurile de capacitate.
Tendinta actuala este ca in locul etaloanelor artificiale sa se foloseasca etaloane naturale. Astfel, pentru etalonul de lungime s-a cautat lungimea de unda a unei radiatii electromagnetice emise in anumite conditii, apoi lungimea drumului parcurs de lumina in vid, intr-un interval precizat de timp.
1.20 Sisteme coerente de unitati
Unitatile pot fi alese arbitrar, insa o astfel de alegere a unei unitati pentru fiecare marime ar conduce la introducerea de noi factori numerici in ecuatiile intre valorile numerice. Este totusi posibila si chiar logica alegerea unui sistem de unitati astfel ca ecuatiile intre valori numerice (cu factorii numerici inclusi) sa aiba aceeasi forma cu ecuatiile corespunzatoare intre marimi. Un sistem de unitati definit in acest mod se numeste coerent in raport cu sistemul de marimi si de ecuatii considerat. Sistemul International de Unitati SI este un astfel de sistem. Acest sistem este dat in ISO 31-1, ISO 31-10, ISO 31-12 si ISO 31-13. Unitatile necoerente sunt legate de cele coerente prin relatii cu coeficienti numerici, ca de exemplu caloria in functie de joule:
![]()
Pentru un sistem anumit de marimi si ecuatii se obtine un sistem coerent de unitati definind mai intai unitatile marimilor fundamentale, adica unitatile fundamentale. Pentru fiecare marime derivata, definitia unitatii derivate corespunzatoare in functie de unitatile fundamentale se da printr-o expresie algebrica obtinuta prin inlocuirea in produsul de dimensiuni a simbolurilor dimensiunilor fundamentale cu simbolurile unitatilor fundamentale. In cazul particular al unei marimi cu dimensiunea unu, unitatea este 1. Intr-un astfel de sistem coerent de unitati, nici un factor numeric diferit de numarul 1 nu figureaza in expresiile unitatilor derivate (date in functie de unitatile fundamentale) - a se vedea exemple in tabelul 2.
Tabelul 2. Unitati derivate intr-un sistem coerent de unitati
|
Marimea |
Ecuatia |
Dimensiunea |
Simbolul unitatii derivate |
|
Viteza |
|
|
|
|
Forta |
|
|
|
|
Energie cinetica |
|
|
|
|
Energie potentiala |
|
|
|
|
Energie mecanica |
|
|
|
|
Randament energetic |
| ||
|
Caldura molara |
|
|
|
|
Fluxul magnetic |
|
|
|
Denumirea Sistem International de Unitati, prescurtat SI, a fost adoptata la a 11-a Conferinta Generala de Masuri si Greutati, in 1960. Romania a aderat la acest sistem prin hotararea Consiliului de Ministri nr.550 din 31 august 1961.
SI cuprinde patru categorii de unitati: 1 - fundamentale; 2 - derivate (grupele a, b si c); 3 - suplimentare; 4 - unitati derivate ce se exprima prin unitati suplimentare. Acestea formeaza impreuna sistemul coerent de unitati SI.
In 1960 CGPM (Conférence Générale des Poids et Mesures) a clasat unitatile pentru unghiul plan (radianul) si unghiul solid (steradianul) in categoria unitatilor suplimentare. In 1980 Comitetul International de Masuri si Greutati a hotarat sa considere clasa unitatilor suplimentare in SI ca o clasa de unitati derivate fara dimensiune. CGPM a lasat libertatea fiecaruia de a le utiliza sau nu in expresiile unitatilor SI derivate. Desi in aceaste conditii unitatea coerenta pentru unghiul plan si pentru unghiul solid este numarul 1, in cele mai multe aplicatii se utilizezeaza totusi denumirile speciale radian si steradian in locul numarului 1. In continuare vom considera unitatile suplimentare in cadrul unitatilor derivate cu denumiri speciale, astfel vor fi numai doua categorii de unitati - fundamentale si derivate.
1. Unitatile fundamentale sunt: lungimea (unitatea metru, simbol m), masa (kilogram, kg), timpul (secunda, s), curentul electric (amper, A), temperatura termodinamica (kelvin, K), cantitatea de substanta (mol, mol), intensitatea luminoasa (candela, cd).
Definitiile unitatilor fundamentale
Metrul reprezinta lungimea drumului parcurs de
lumina in vid, intr-un interval de timp de ![]() dintr-o secunda.
dintr-o secunda.
Prototipul kilogramului ramane cel confirmat de prima Conferinta Generala de Masuri si Greutati, de la Paris din 1889. Este confectionat din platina iridiata.
Secunda reprezenta durata a ![]() perioade ale radiatiei
corespunzatoare tranzitiei intre cele doua niveluri hiperfine ale starii
fundamentale a atomului de cesiu 133.
perioade ale radiatiei
corespunzatoare tranzitiei intre cele doua niveluri hiperfine ale starii
fundamentale a atomului de cesiu 133.
Kelvinul reprezinta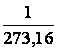 din temperatura termodinamica a punctului triplu al apei.
din temperatura termodinamica a punctului triplu al apei.
Molul reprezinta cantitatea de substanta dintr-un
sistem ce contine atatea entitati elementare (atomi, molecule, grupari de
molecule etc.) cati atomi contine o masa de ![]() de carbon 12, adica un numar de atomi egal cu numarul lui
Avogadro
de carbon 12, adica un numar de atomi egal cu numarul lui
Avogadro ![]() .
.
Amperul reprezinta intensitatea curentului
electric constant care, mentinut in doua conductoare paralele, rectilinii, de
lungime infinita, de sectiunea circulara neglijabila, asezate in vid la o
distanta de ![]() unul de celalalt, ar produce intre cele doua conductoare o
forta de
unul de celalalt, ar produce intre cele doua conductoare o
forta de ![]() pe unitatea de
lungime.
pe unitatea de
lungime.
Candela este intensitatea luminoasa, intr-o
directie data, a unei surse care emite o radiatie monocromatica cu frecventa de
![]() si a carei intensitate
radianta in acea directie este
si a carei intensitate
radianta in acea directie este ![]() dintr-un watt pe steradian.
dintr-un watt pe steradian.
Aceste unitati fundamentale, ca si etaloanele lor, nu sunt stabilite o data pentru totdeauna prin definitiile enuntate mai sus. Este posibil ca in urma cercetarilor din domeniile de varf ale fizicii (corp solid, fizica nucleara etc.) sa se impuna elaborarea altor unitati fundamentale.
2. Unitati derivate
Expresiile unitatilor derivate coerente in functie de unitatile fundamentale se pot obtine din expresiile produselor de dimensiuni si utilizand urmatoarele substituiri formale:
![]()
Se admite folosirea unor anumite combinatii sau a anumitor denumiri speciale pentru a deosebi marimile care au aceeasi dimensiune. Se pot distinge trei grupe de unitati derivate, notate in continuare cu a), b) si c)
a) unitati derivate exprimate prin unitatile
fundamentale: aria ![]() , volumul
, volumul ![]() , viteza
, viteza ![]() , acceleratia
, acceleratia ![]() , numarul de unda
, numarul de unda ![]() , densitatea
, densitatea ![]() , densitatea de curent
, densitatea de curent ![]() , intensitatea campului magnetic
, intensitatea campului magnetic ![]() , concentratia cantitatii de substanta
, concentratia cantitatii de substanta ![]() .
.
b) Unitati derivate cu denumiri speciale (tabelul 3)
Tabelul 3. Unitati SI derivate cu denumiri speciale, incluzand si unitatile SI suplimentare
|
Marimea derivata |
Unitatea SI derivata |
||
|
Denumire speciala |
Simbol |
Expresie in functie de unitati SI fundamentale si/sau SI derivate |
|
|
unghi plan |
radian |
|
|
|
unghi solid |
steradian |
|
|
|
frecventa |
hertz |
|
|
|
forta |
newton |
N |
|
|
presiune, tensiune mecanica |
pascal |
Pa |
|
|
enrgie, lucru mecanic, cantitate de caldura |
joule |
J |
|
|
putere, flux radiant |
watt |
W |
|
|
sarcina electrica, cantitate de electricitate |
coulomb |
C |
|
|
potential electric, diferenta de potential, tensiune electrica, tensiune electromotoare |
volt |
V |
|
|
capacitate electrica |
farad |
F |
|
|
rezistenta electrica |
ohm |
|
|
|
conductanta electrica |
siemens |
S |
|
|
flux al inductiei magnetice |
weber |
Wb |
|
|
inductie magnetica |
tesla |
T |
|
|
inductanta |
henry |
H |
|
|
temperatura Celsius |
grad Celsius |
°C |
|
|
flux luminos |
lumen |
lm |
|
|
iluminare |
lux |
lx |
|
Dintre unitatile S.I. derivate care contin si unitati suplimentare, pe
langa cele cu denumiri speciale (lumen si lux), enumeram viteza unghiulara ![]() , acceleratia unghiulara
, acceleratia unghiulara ![]() , intensitatea energetica
, intensitatea energetica![]() , luminanta energetica
, luminanta energetica ![]() .
.
Definitia unitatilor suplimentare S.I.
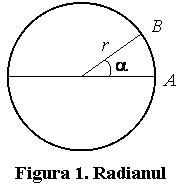 Unghiul plan (simbol
Unghiul plan (simbol ![]() ) este unghiul dintre doua semidrepte care pornesc din
acelasi punct. Se defineste ca raportul dintre lungimea arcului subintins pe un
cerc (cu centrul in punctul considerat) si lungimea razei cercului, prin
formula:
) este unghiul dintre doua semidrepte care pornesc din
acelasi punct. Se defineste ca raportul dintre lungimea arcului subintins pe un
cerc (cu centrul in punctul considerat) si lungimea razei cercului, prin
formula:
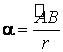 , (1.19)
, (1.19)
unde ![]() este arcul subantins
de laturile unghiului la centru, iar
este arcul subantins
de laturile unghiului la centru, iar ![]() este raza cercului
(fig.1).
este raza cercului
(fig.1).
Unitatea
de unghi plan este radianul, care reprezinta unghiul
plan cuprins intre doua raze ce delimiteaza pe circumferinta unui cerc
un arc de lungime egala cu cea a razei![]() . Unghiul plan maxim exprimat in radiani corespunde unui arc
de lungime
. Unghiul plan maxim exprimat in radiani corespunde unui arc
de lungime ![]() , si are valoarea
, si are valoarea ![]()
Unghiul solid (simbol![]() ) este unghiul solid al unui con. Se defineste ca raportul
intre aria delimitata pe suprafata unei sfere (avand centrul in varful conului)
si patratul razei sferei, prin formula:
) este unghiul solid al unui con. Se defineste ca raportul
intre aria delimitata pe suprafata unei sfere (avand centrul in varful conului)
si patratul razei sferei, prin formula:
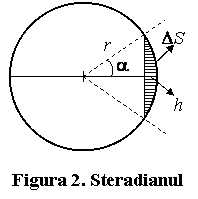
![]() (1.20)
(1.20)
unde ![]() este suprafata
intersectata pe o sfera de raza
este suprafata
intersectata pe o sfera de raza ![]() de un con cu unghiul
la varf
de un con cu unghiul
la varf ![]() , avand varful in
centrul sferei (fig.2). Unitatea de unghi
solid este steradianul. Un steradian reprezinta unghiul solid care, avand varful in centrul unei sfere,
delimiteaza pe suprafata acestei sfere o arie egala cu cea a unui patrat a
carui latura este egala cu raza sferei
, avand varful in
centrul sferei (fig.2). Unitatea de unghi
solid este steradianul. Un steradian reprezinta unghiul solid care, avand varful in centrul unei sfere,
delimiteaza pe suprafata acestei sfere o arie egala cu cea a unui patrat a
carui latura este egala cu raza sferei ![]() . De la geometrie se stie ca aria segmentului de sfera
. De la geometrie se stie ca aria segmentului de sfera ![]() este data de formula
este data de formula ![]() , unde
, unde ![]() reprezinta inaltimea
calotei sferice, astfel ca
reprezinta inaltimea
calotei sferice, astfel ca
![]() .
.
Conform definitiei, formula unghiului solid ![]() va fi:
va fi:
![]() , (1.21)
, (1.21)
de unde prin diferentiere obtinem:
![]() . (1.22)
. (1.22)
Formula (1.21) indica relatia dintre unghiul solid ![]() si unghiul plan
si unghiul plan ![]() .
.
c) Unitati derivate care se exprima folosind denumiri speciale (tabelul 4)
Tabelul 4. Unitati SI derivate cu folosirea denumirilor speciale
|
Marimea derivata |
Unitatea SI derivata |
||
|
Denumirea unitatii in SI |
Simbol |
Expresia in unitati SI fundamentale |
|
|
momentul fortei |
metru- newton |
|
|
|
densitate de flux termic, iluminare energetica |
watt pe metru patrat |
|
|
|
capacitate termica |
joule pe kelvin |
|
|
|
capacitate termica masica |
joule pe kilogram kelvin |
|
|
|
energie masica |
joule pe kilogram |
|
|
|
energie volumica |
joule pe metru cub |
|
|
|
intensitate a campului electric |
volt pe metru |
|
|
|
sarcina electrica volumica |
coulomb pe metru cub |
|
|
|
permitivitate |
farad pe metru |
|
|
|
permeabilitate |
henry pe metru |
|
|
|
energie molara |
joule pe mol |
|
|
|
capacitate termica molara |
joule pe mol kelvin |
|
|
Din tabelul 4 se poate observa avantajul utilizarii de simboluri sau
denumiri speciale in expresiile unitatilor compuse. Astfel, utilizand unitatea
derivata volt (![]() ), simbolul unitatii SI pentru permitivitate se poate scrie sub
forma mai simpla
), simbolul unitatii SI pentru permitivitate se poate scrie sub
forma mai simpla ![]() . Utilizand unitatea derivata joule (
. Utilizand unitatea derivata joule (![]() ), simbolul unitatii SI pentru entropia molara se poate scrie sub forma simpla
), simbolul unitatii SI pentru entropia molara se poate scrie sub forma simpla ![]() ;
;
Unitatea unu
Unitatea coerenta a oricarei marimi cu dimensiune unu este unitatea unu, simbol 1. In general, acest numar nu se scrie in mod explicit cand se exprima valoarea unei asemenea marimi (cu exceptia unor marimi cu denumiri speciale, cand, in functie de context, pot fi sau nu utilizate). Exemple:
indicele de refractie ![]() , unghi plan
, unghi plan ![]() unghi solid
unghi solid ![]() .
.
Simbolurile marimilor
Sunt constituite dintr-o singura litera a alfabetului latin sau grec, uneori cu indice interior sau alte semne distinctive. Se tiparesc cu caractere italice, indiferent de caracterele folosite in text. Indicii inferiori care reprezinta simbolul unei marimi fizice se tipareste tot cu caracter italic, ca si marimea. Ceilalti indici inferiori se tiparesc cu caractere romane drepte.
Exemplul 5
|
Indici italici |
|
|
|
|
Indici drepti |
|
|
|
Simbolurile marimilor trebuie tiparite cu litere mici, in afara acelor marimi pentru care denumirea deriva de la un nume propriu ca de exemplu:
m (metru); s (secunda); A (amper); Wb (weber)
1.21 Unitatile speciale
Se introduc pentru situatii speciale intalnite in anumite fenomene.
Exemplul 6
Torrul se foloseste ca unitate de presiune deoarece presiunile joase se masoara cu manometrul cu mercur. Expresia torrului este:
![]()
Ora se foloseste curent pentru masurarea timpului in activitatile umane zilnice:
![]()
Tabelul 5. Prefixe pentru multiplii si submultiplii zecimali ai unitatilor SI
|
Factorul |
Prefixul |
Factorul |
Prefixul |
||
|
Denumire |
Simbol |
Denumire |
Simbol |
||
|
|
yotta |
Y |
|
yocto |
y |
|
|
zetta |
Z |
|
zepto |
z |
|
|
exa |
E |
|
atto |
a |
|
|
peta |
P |
|
femto |
f |
|
|
tera |
T |
|
pico |
p |
|
|
giga |
G |
|
nano |
n |
|
|
mega |
M |
|
micro | |
|
|
kilo |
k |
|
mili |
m |
|
|
hecto |
h |
|
centi |
c |
|
|
deca |
da |
|
deci |
d |
Bibliografie
1. Mircea Oncescu. Marimi si Unitati in Fizica, vol.I. Editura Tehnica, Bucuresti, 1955
2. Traian I. Cretu, Corneliu Ghizdeanu. Metode de masurare si prelucrare a datelor experimentale - pentru uzul studentilor. Institutul Politehnic Bucuresti, 1980
3. Traian I. Cretu. Fizica Generala Vol.I. Editura Tehnica, Bucuresti, 1986
Jerome V. Scholle. Metrology. Addison Wesley Longman Inc., 1993
5. Institutul Roman de Standardizare. Unitati de Masura. Colectie de standarde. Editura Tehnica, Bucuresti, 1997
Arjana
Davidescu. Metrologie generala, Ed. Politehnica,
7. Preben Horwath, Fiona Redgrave. Metrology - in short, 2nd edition, MKom Aps, Denmark, 2003
8. Jay L. Bucher (editor), The Metrology Handbook, Measurement Quality Division, ASQ, 2004
|