ALTE DOCUMENTE |
Pachete de unde. Viteza de faza. Viteza de grup.
Undele
electromagnetice de forma (7.6) si (7.7), in care pulsatia ![]() a undei este egala cu pulsatia oscilatorului,
se numesc unde electromagnetice
monocromatice, si se pot obtine numai in ipoteza ca miscarea oscilatorului
se petrece pe timp nelimitat. In realitate insa, un oscilator scos din starea
de echilibru nu poate oscila decat un interval de timp finit, din cauza
faptului ca in procesul de oscilatie oscilatorul pierde in mod continuu energie
prin radiatie.
a undei este egala cu pulsatia oscilatorului,
se numesc unde electromagnetice
monocromatice, si se pot obtine numai in ipoteza ca miscarea oscilatorului
se petrece pe timp nelimitat. In realitate insa, un oscilator scos din starea
de echilibru nu poate oscila decat un interval de timp finit, din cauza
faptului ca in procesul de oscilatie oscilatorul pierde in mod continuu energie
prin radiatie.
Se poate
trage concluzia ca un oscilator constituie o sursa de unde electromagnetice,
intr-un interval de timp ![]() . In fig.3 este reprezentata grafic in functie de timp intensitatea
campului electric, intr-un punct din spatiu, pentru un oscilator care emite
unde electromagnetice: 626j93g
. In fig.3 este reprezentata grafic in functie de timp intensitatea
campului electric, intr-un punct din spatiu, pentru un oscilator care emite
unde electromagnetice: 626j93g


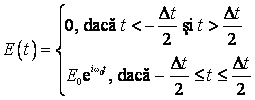 (7.23)
(7.23)
Este
simplu de aratat ca in acest caz unda electromagnetica nu este monocromatica,
intrucat ea contine unde electromagnetice monocromatice de pulsatii ![]() , situate
intr-un domeniu mai mult sau mai putin restrans in jurul valorii
, situate
intr-un domeniu mai mult sau mai putin restrans in jurul valorii ![]() . Confrom
teoriei privind dezvoltarea in integrale Fourier, intensitatea campului
electric in unda monocromatica de pulsatie
. Confrom
teoriei privind dezvoltarea in integrale Fourier, intensitatea campului
electric in unda monocromatica de pulsatie ![]() este data de relatia:
este data de relatia:
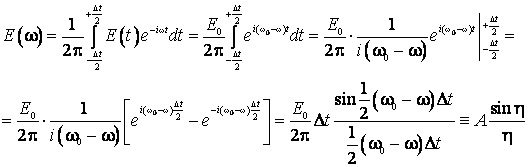 (7.24)
(7.24)
unde s-au introdus urmatoarele notatii:
![]() (7.25)
(7.25)
Intensitatea undei fiind proportionala cu patratul amplitudinii, se poate scrie:
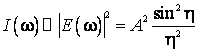 (7.26)
(7.26)
Dupa cum se stie, functia
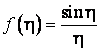 (7.27)
(7.27)
Prezinta un maxim principal pentru ![]() ; pentru
; pentru ![]() unde
unde ![]() , are
valoarea zero, iar conditia de maxim secundar se obtine din relatia:
, are
valoarea zero, iar conditia de maxim secundar se obtine din relatia:
![]() (7.28)
(7.28)
Solutiile ecuatiei (7.28), precum si valorile maximelor corespunzatoare sunt indicate in Tabelul 1.
Tabelul 1. Valorile maxime ale functiei 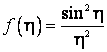
|
|
|
|
|
4,47 |
|
|
|
Forma intensitatii ![]() este aratata in fig.4. Se observa ca functia
este aratata in fig.4. Se observa ca functia ![]() prezinta un maxim principal pentru
prezinta un maxim principal pentru ![]() . Neglijand
maximele secundare, erorile comise sunt sub 5%, astfel ca putem considera
intreaga intensitate a unei cuprinsa in intervalul de frecvente
. Neglijand
maximele secundare, erorile comise sunt sub 5%, astfel ca putem considera
intreaga intensitate a unei cuprinsa in intervalul de frecvente ![]() , unde
, unde ![]() , sau
, sau ![]() . Daca luam
in considerare si maximele secundare, atunci relatia intre
. Daca luam
in considerare si maximele secundare, atunci relatia intre ![]() si
si ![]() se va scrie
se va scrie ![]() , de unde
se observa ca daca durata
, de unde
se observa ca daca durata ![]() a radiatiilor cuasimonocromatice este mai
mare, intervalul spectral
a radiatiilor cuasimonocromatice este mai
mare, intervalul spectral ![]() este mai mic.
este mai mic.


Daca se tine cont si de maximele secundare, conditia anterioara devine:
![]() (7.29)
(7.29)
astfel ca largimea domeniului spectral este invers proportionala cu intervalul de timp in care are loc oscilatia armonica a sursei de unde.
In cazul ![]() , ceea ce
inseamna ca numai oscilatiile armonice nelimitate in timp pot genera unde
electromagnetice monocromatice. Cu cat intervalul de timp
, ceea ce
inseamna ca numai oscilatiile armonice nelimitate in timp pot genera unde
electromagnetice monocromatice. Cu cat intervalul de timp ![]() in care se desfasoara oscilatia este mai mic,
cu atat domeniul pulsatiilor
in care se desfasoara oscilatia este mai mic,
cu atat domeniul pulsatiilor ![]() este mai mare.
este mai mare.
S-a aratat
ca datorita fenomenului de dispersie, viteza de propagare a fazei undei
electromagnetice depinde de pulsatia ![]() . Vom
studia o unda rezultata in urma propagarii unei perturbatii de durata finita, a
carei pulsatie este cuprinsa in intervalul
. Vom
studia o unda rezultata in urma propagarii unei perturbatii de durata finita, a
carei pulsatie este cuprinsa in intervalul
![]() (7.30)
(7.30)
iar modulul vectorului de unda este cuprin in intervalul:
![]() (7.31)
(7.31)
Pentru ![]() se poate dezvolta in serie functia
se poate dezvolta in serie functia ![]() , din care
se opreste numai termenul de ordinul intai:
, din care
se opreste numai termenul de ordinul intai:
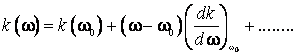 (7.32)
(7.32)
Unda rezultata va fi o suprapunere de unde armonice plane, de forma:
![]() (7.33)
(7.33)
cu pulsatiile cuprinse in intervalul (7.30), si respectiv cu modulul vectorului de unda cuprins in intervalul de valori (7.31):
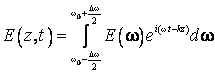 (7.34)
(7.34)
Pentru un domeniu de pulsatii suficient de ingust in jurul
pulsatiei ![]() , se poate
considera ca
, se poate
considera ca ![]() este constant si este egal cu
este constant si este egal cu ![]() :
:
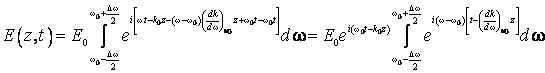 (7.35)
(7.35)
Expresia (7.35) se simplifica daca se introduc notatiile:
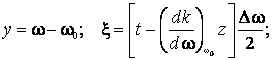 (7.36)
(7.36)
Cu aceste notatii, intensitatea campului electric al undei se va scrie:
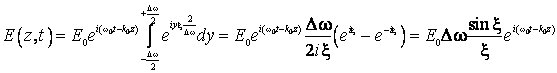
Se ajunge astfel la concluzia ca, prin suprapunerea undelor
armonice dintr-un domeniu ingust de pulsatii, se obtine o unda armonica plana
modulata in amplitudine cu factorul ![]() . Aceasta
conduce la faptul ca, la un moment dat, amplitudinea undei este diferita de
zero numai intr-un domeniu restrans din spatiu. Asadar, suprapunerea undelor cu pulsatii apropiate, cuprinse intr-un
domeniu restrans in jurul pulsatiei
. Aceasta
conduce la faptul ca, la un moment dat, amplitudinea undei este diferita de
zero numai intr-un domeniu restrans din spatiu. Asadar, suprapunerea undelor cu pulsatii apropiate, cuprinse intr-un
domeniu restrans in jurul pulsatiei ![]() , conduce
la formarea pachetelor de unda sau a trenurilor de unda.
, conduce
la formarea pachetelor de unda sau a trenurilor de unda.
Pentru pachetele de unda se face distinctie intre viteza de
faza ![]() si viteza de grup
si viteza de grup ![]() , care
reprezinta viteza de propagare a suprafetei de egala amplitudine.
, care
reprezinta viteza de propagare a suprafetei de egala amplitudine.
Ecuatia suprafetei de faza este:
![]() (7.38)
(7.38)
de unde:
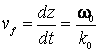
In general, pentru o frecventa oarecare se poate scrie:
![]() (7.39)
(7.39)
Ecuatia suprafetei de egala amplitudine este:
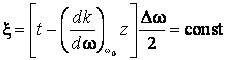
de unde:
![]() (7.40)
(7.40)
Mediul
este nedispersiv daca viteza de faza ![]() nu depinde de pulsatia
nu depinde de pulsatia ![]() .
.
Din (7.39) si (7.40) se obtine:
![]() (7.41)
(7.41)
Avand in vedere relatiile ![]() , se
obtine:
, se
obtine:
![]() (7.42)
(7.42)
Expresie cunoscuta sub denumirea de formula lui Rayleigh.
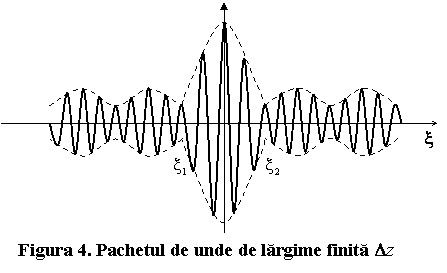

Pachetul
de unde (fig.4) are o largime ![]() , care este
functie de largimea benzii de pulsatie
, care este
functie de largimea benzii de pulsatie ![]() .
.
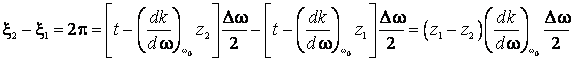
sau
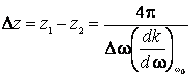 (7.43)
(7.43)
In
concluzie, pachetul de unde este cu atat mai larg, cu cat ![]() este mai mic. Daca unda este monocromatica,
este mai mic. Daca unda este monocromatica, ![]() , si
, si ![]() , adica
unda armonica plana se intinde in intregul spatiu, de la
, adica
unda armonica plana se intinde in intregul spatiu, de la ![]() la
la ![]() .
.
Intr-un
interval de timp ![]() pachetul de unde se deplaseaza pe o distanta
pachetul de unde se deplaseaza pe o distanta ![]() :
:
![]() , sau
, sau ![]() (7.44)
(7.44)
Pe baza formulei (7.29) este adevarata relatia:
![]() (7.45)
(7.45)
sau, in general, se obtine:
![]() (7.46)
(7.46)
Formulele (7.29) si (7.46) reprezinta, de fapt, relatii de nedeterminare.
Exemplul 1
Sa se demonstreze ca intre viteza de faza si viteza de grup exista relatia:
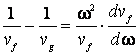
Rezolvare
Folosind formulele (7.39). (7.40) si (7.42), se poate scrie:
![]() (7.47)
(7.47)
deoarece ![]() si
si ![]() . In
continuare, se poate scrie:
. In
continuare, se poate scrie:
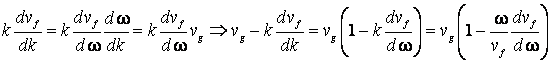 (7.48)
(7.48)
Din (7.47) si (7.48) rezulta:
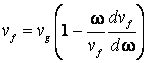
de unde rezulta relatia care trebuia demonstrata.
|