Potentialul electric

Campul electric poate fi caracterizat nu numai de marimea vectoriala , ci si de o marime scalara , numita potential electric.

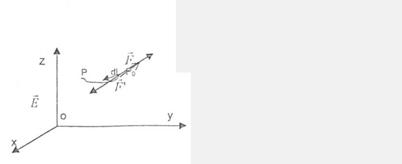
Pentru a defini potentialul campului electric, sa consideram o sarcina de proba q₀ intr-un camp electrostatic oarecare (fig.10.1). In fiecare punct al campului asupra sarcinii q₀ actioneaza forta . Pentru a deplasa 858b16i aceasta sarcina fara acceleratie in campul electric, asupra ei trebuie sa se actioneze o forta de egala si de sens opus fortei , potrivit cu legea de conservare aimpulsului studiata anterior. La deplasarea sarcinii q₀ intre punctele P₀ si P se efectueaza lucrul mecanic:

W =   (10.1)

Fig.10.1. Pentru deducerea expresiei potentialului electric

Lucrul mecanic efectuat la deplasarea fara acceleratie a unitatii de sarcina in campul electric din punctul P₀ in punctul P este dat de relatia:

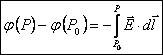(10.2)

Marimea definita de (10.2) poarta numele de potential electric al punctului P.

Potentialul electric se masoara in Volti.

Aceasta relatie permite calcularea diferentei de potential intre punctele P si P₀. Pentru a putea calcula potentialul in orice punct:

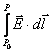= - + (10.2`)

trebuie sa se aleaga o valoare pentru potentialul punctului de referinta P₀. Prin conventie, potentialul punctelor situate la infinit se considera zero. Daca punctul P₀ este indepartat la infinit atunci si din relatia (10.2`) rezulta ca:

(10.3)

Potentialul unei sarcini punctiforme q la distanta r de sarcina se calculeaza cu ajutorul formulei (10.3):

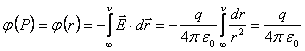(10.5)

Campul electrostatic este un camp conservativ

Campul electrostatic este generat de sarcini punctiforme sau distributii de sarcina in repaus si constante in timp.

10.2.Campul si potentialul electric al unui conductor incarcat cu sarcina

Din punct de vedere al proprietatilor electrice materialele se impart in: - - conductori

semiconductori si

izolatori.

Delimitarea intre aceste trei grupe nu este insa neta, deoarece marirea temperaturii peste anumite valori poate modifica proprietatile electrice in asa masura incat un izolator poate deveni semiconductor sau chiar conductor.

In cazul metalelor purtatorii de sarcina sunt electronii liberi proveniti din electronii de valenta care parasesc atomii si se misca dezordonat prin reteaua cristalina.

Consideram un conductor metalic incarcat electric pozitiv, adica cu un deficit de electroni fata de sarcinile existente in corp in conditii de neutralitate electrica. Presupunem ca sarcina pozitiva este in

Existenta miscarii dezordonate a electronilor liberi nu influenteaza starea de echilibru electrostatic. Un camp electric, oricat de slab ar fi, ar duce la aparitia unei miscari ordonate a electronilor liberi. Daca in conductor nu au loc deplasari ordonate de sarcina electrica putem afirma ca intensitatea campului electric in interiorul sau este nula:

(10.15)

Intrucat campul electric este dat de derivate potentialului, rezulta ca:

= const. (10.16)

in toate punctele din interiorul conductorului. Cu alte cuvinte volumul conductorului incarcat electric este o regiune echipotentiala.

Aplicand legea lui Gauss pentru o suprafata inchisa din interiorul conductorului incarcat cu sarcina +q (Fig.10.4.) rezulta, tinand seama de relatia (10.15):

(10.17)

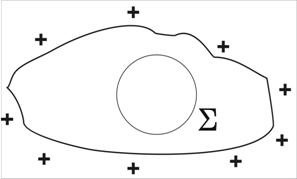
Fig.10.4. Sarcina electrica este repartizata numai la suprafata conductorului

deci in interiorul suprafetei nu exista sarcina electrica.

Alegand suprafata gaussiana chiar suprafata conductorului, putem afirma ca sarcina electrica cu care este incarcat conductorul nu se afla in interiorul sau ci repartizata in regiunea pe suprafata. Orice punct de pe suprafata are o densitate de sarcina superficiala

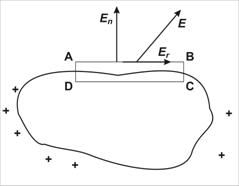
Fig.10.5. Directia campului electrostatic este normala la suprafata conductorului

10.3.Capacitatea electrica

La incarcarea unui conductor cu sarcina de diferite valori se constata ca potentialul electric al conductorului se modifica, dar raportul ramane constant. Marimea:

C = (10.19)

poarta numele de capacitate electrica a conductorului.

Capacitatea electrica se masoara in farazi (F).

Avand mai multi conductori de capacitati diferite incarcati la acelasi potential, pe conductorul cu capacitatea cea mai mare se afla inmagazinata sarcina electrica cea mai mare.

Sarcina electrica poate fi inmagazinata de un singur conductor izolat cat si de ansambluri de conductoare.

Sa analizam cazul condensatorului plan, care este alcatuit din doua placi conductoare plane si paralele, de arie S, asezate la distanta d si incarcate cu sarcini egale si de semne contrare (Fig.10.6). Exceptand regiunea de margine a domeniului dintre placi, campul electric in interior este uniform si valoarea lui se poate calcula cu relatia (10.18):

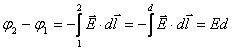(10.20)

Dar intensitatea campului intre placi poate fi exprimata prin relatia (10.17), astfel ca putem scrie:

sau

C = (10.21)

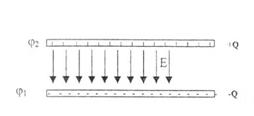
Fig.10.6. Condensatorul plan

Relatia (10.21) exprima capacitatea electrica a condensatorului plan.

Daca cele doua conductoare au forma cilindrica sau sferica condensatorul se numeste respectiv cilindric sau sferic.

INTREBARI

1.Potentialul unui punct plasat la infinit este considerat nul. S-ar putea considera si o alta valoare? De ce?

a) Se poate considera orice valoare, este vorba de o conventie. Atribuirea valorii zero simplifica operatiile matematice si interpretarea fizica.

b)Nu se poate considera o alta valoare, pentru ca s-ar modifica valorile potentialului.

c) Se poate considera orice valoare, deducerea expresiei potentialului electric se face , de fapt, pentru o diferenta de potential.

d) Fiind vorba de o conventie se poate lua orice valoare, fara a se modifica potentialul.

e) Nu se poate considera alta valoare pentru ca se modifica definitia potentialului.

2. Daca in loc ca potentialului unui punct situat la infinit sa i se atribuie valoarea zero i se atribuie o valoare mai mare cu p%, ce modificari sufera valoarea potentialului intr-un punct oarecare?

a) nu se modifica,

b) creste cu p%,

c) scade cu p%,

d) se multiplica de p% ori,

e) se micsoreaza de p% ori.

3. Campul electrostatic este un camp conservativ. Dece?

a) pentru ca este generat de sarcini punctiforme,

b) pentru ca este generat de distributii de sarcina in repaus si constante in timp,

c) pentru ca lucrul mecanic efectuat la deplasarea unor sarcini nu depinde de drumul urmat,

d) pentru ca lucrul mecanic efectuat la deplasarea unor sarcini nu depinde de drumul urmat,

e) pentru ca lucrul mecanic efectuat la deplasarea unor sarcini depinde numai de pozitiile intre care se deplaseaza sarcinile.

4. Care este valoarea campului electric si a potentialului electric in interiorul unui conductor incarcat?

a) campul electric este nul, potentialul are aceeasi valoare cu potentialul de la suprafata conductorului,

b) campul electric si potentialul au aceeasi valoare cu cele de la suprafata conductorului,

c) valorile acestora depind de cantitatea de sarcina de pe conductor,

d) valorile acestora depind de cantitatea de sarcina din conductor,

e) valorile acestora depind de cantitatea totala de sarcina de pe si din conductor.

5.Capacitatea electrica se poate defini prin relatia:

a) C = q/φ, unde cu q este notata valoarea unei sarcini electrice iar cu φ potentialul,

b) C = q .φ, unde cu q este notata valoarea unei sarcini electrice iar φ este potentialul

c) C = q - , unde cu q este notata valoarea unei sarcini electrice iar este potentialul,

d) C = /q, unde cu este notata valoarea unei sarcini electrice iar cu q potentialul,

e) C = - q, unde cu este notata valoarea unei sarcini electrice iar cu q potentialul.