Principiul relativitatii in mecanica clasica. Transformarile lui Galilei. Clasificarea sistemelor de referinta

Principiul relativitatii in mecanica clasica. Transformarile lui Galilei. Clasificarea sistemelor de referinta

Sa prezentam pentru inceput procedeul clasic de transformare a rezultatelor masuratorilor marimilor spatiu si timp la trecerea de la un la alt . Se va arata ca acest procedeu este valabil cu buna aproximatie si in TRR in conditii terestre, unde vitezele de deplasare sunt mult mai mici decat vitez 545j96f a luminii in vid .

Consideram un sistem de coordonate cartezian aflat in repaus, si alt sistem de coordonate care se deplaseaza rectiliniu si uniform de-a lungul axei cu viteza constanta fata de (fig.1). Presupunem ca in timpul deplasarii axele de coordonate ale sis­temelor si raman para­lele intre ele, iar la mo­mentul originile lor si coincid. Admitem de asemenea ca un ceas in repaus fata de indica in­tervalul de timp , iar ceasul aflat in repaus fata de indica in­tervalul de timp . Fata de observatorul aflat in repaus in raport cu distanta va fi egala cu , si astfel in raport cu avem:

Fata de observatorul aflat in repaus in raport cu distanta va fi egala cu . Prin urmare, in raport cu acesta se poate scrie relatia:

(4.2)

Din (3.1) si (3.2) se obtine:

(4.3)

Ajungem astfel la concluzia ca timpul este absolut, indepen­dent de starea de miscare a sistemului de referinta, adica cele doua ceasuri legate rigid de sisteme de referinta diferite, aflate in mis­care unul in raport cu celalalt, indica acelasi interval de timp. Din cele relatate nu rezulta ca am demonstrat relatia (4.3), deoarece am folosit in mod implicit ipoteza clasica, ad­misa fara demonstratie, ca distanta intre doua puncte este o marime absoluta, independenta fata de sistemul de referinta. Postuland caracterul absolut al timpu­lui prin egalitatea (4.3), se ajunge la natura absoluta a lungimilor. Valabilitatea carac­terului absolut al timpului, respectiv al spatiului, poate fi pro­bata numai in masura concordantei cu datele experimentale.

Relatiile (4.1) si (4.2) reprezinta transformarile lui Galilei, care se scriu pentru componentele vectorilor , si sub forma :

(4.4)

respectiv

(4.5)

Ultimele expresii pot fi scrise si sub forma matriciala, in acest scop fiind comod sa utilizam notatiile , si respectiv :

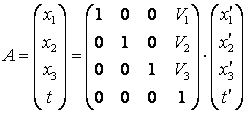(4.6)

si

(4.7)

Se verifica simplu ca produsul matricelor de transformare si este matricea unitate.

Subliniem faptul ca relatia (4.3) este o consecinta a unei ipoteze fundamentale a fizicii clasice, si anume ipoteza propagarii instanta­nee cu viteza infinita a interactiilor. Existenta unei viteze in­finite de propagare a interactiilor permite sincronizarea tuturor ceasurilor, legate de orice sistem de referinta. De asemenea, din (4.3) rezulta caracterul absolut al notiunii de simultaneitate, adica doua evenimente simultane in raport cu un sistem de referinta sunt simultane in raport cu orice alt sistem de referinta.

Consideram viteza punctului material fata de sistemul de referinta :

(4.8)

si

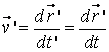(4.9)

viteza aceluiasi punct material in raport cu .

Derivand in raport cu timpul relatia (4.1) obtinem:

(4.10)

respectiv

(4.11)

Formula (4.10) sau (4.11) reprezinta legea de compunere a vitezelor in mecanica clasica.

Derivand (4.11) obtinem:

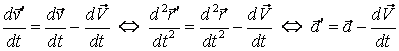(4.12)

Din (4.12) observam ca este posibila clasificarea sistemelor de referinta in doua categorii: cele in care se respecta principiul inertiei (sau inertiale) si cele in care nu se respecta principiul inertiei (neinertiale).

a) In cazul = constant, , si , de unde rezulta . Se observa usor ca daca principiul inertiei se respecta fata de sistemul , principiul se respecta si fata de :

(4.13)

(4.14)

De aici se pot trage urmatoarele concluzii:

- daca exista un singur sistem de referinta inertial , atunci pot exista o infinitate de asemenea sisteme, fiecare dintre ele deplasandu-se fata de sistemul initial cu o viteza diferita;

- din (4.13) si (4.14) se poate afirma ca toate sunt echivalente intre ele, deoarece legea intai a dinamicii, cat si legea a doua a dinamicii au aceeasi forma fata de orice .

b) Cazul , in care principiul intai al dinamicii nu se mai respecta, si aceste sisteme de referinta se numesc neinertiale :

(4.15)

Daca . Se observa de asemenea din (4.15) ca intr-un legea a doua isi schimba forma fata de forma intr-un . In concluzie, orice sistem de referinta care se deplaseaza accelerat fata de un sistem de referinta inertial este un .

Se poate arata din (3.1) ca distanta dintre doua puncte oarecare din spatiu este invarianta fata de transformarile Galilei, iar din (4.10)-(4.11) se poate arata ca si vitezele relative a doua corpuri oarecare sunt invariante. De aici rezulta invarianta fortelor ce depind de distanta sau de vitezele relative, ca de exemplu forta atractiei universale ce depinde de distanta dintre centrele a doua corpuri de mase si , sau fortele de frecare ce depind de viteza relativa a corpurilor aflate in contact. In mecanica fortele depind de obicei numai de dis­tantele relative dintre corpuri si respectiv de vitezele lor rela­tive, si astfel acestea sunt identice in raport cu sistemele de refe­rinta si respectiv :

(4.16)

Prin derivarea de doua ori in raport cu timpul a formulelor (4.4) si (4.5) rezulta ca si acceleratiile corpurilor sint aceleasi in raport cu cele doua sisteme de referinta:

(4.17)

Am aratat astfel ca fortele si acceleratiile sint invariante fata de trans­formarile Galilei. Aceasta reflecta faptul ca miscarea oricarui punct material are loc identic fata de referentialele si , in cazul unor conditii initiale identice. Ajungem astfel la concluzia care reprezinta principiul relativitatii in mecanica Newtoniana:

'Miscarea rectilinie si uniforma a sistemelor de referinta inertiale nu influenteaza desfasurarea proceselor mecanice in aceste sisteme'. Principiul relativitatii lui Galilei subliniaza deci echivalenta tuturor in mecanica Newtoniana. De cele mai multe ori se considera cazul simplificat cind sistemul de referin­ta se deplaseaza in lungul axei in raport cu . In con­ditiile , transformarile lui Galilei (4.4) si (4.5) iau forma:

(4.18)

respectiv

(4.19)