Producerea, propagarea si proprietatile undelor electromagnetice
In teoria electromagnetismului
clasic, elaborata de Maxwell, se arata ca daca o particula incarcata cu sarcina
electrica 
, aflata in
vid, se deplaseaza accelerat cu acceleratia 
, atunci
din punctul in care se afla particula la un moment 
se propaga o unda electromagnetica sferica, in
ca 828g68i re vectorii 
si 
depind de timp si de distanta fata de sursa
de unde (fig.1).
Intr-un punct oarecare din spatiu M, intensitatea campului electric este suma a doua componente:
- intensitatea campului electric coulombian:
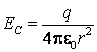(7.1)
- intensitatea campului electric datorat acceleratiei purtatorului de sarcina:
(7.2)
Vectorii 
si sunt perpendiculari intre ei. este paralel cu raza vectoare 
, iar perpendicular pe 
si cuprins in planul format de vectorii si (fig.2).
Datorita scaderii mai
rapide a modulului vectorului cu distanta 
decat modulul vectorului , se poate
determina o distanta 
astfel incat pentru 
sa fie indeplinita conditia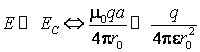 
, de unde
se obtine:
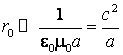(7.3)
Regiunea din spatiu aflata la o distanta fata de particula cu sarcina se numeste zona
de unda, si in aceasta zona se poate neglija componenta campului
coulombian. In punctul M intensitatea campului magnetic generat de particula ce
poarta sarcina electrica este data de formula:
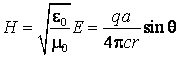(7.4)
Considerand o miscare oscilatorie armonica efectuata pe axa Oz de particula generatoare de camp, elongatia si acceleratia miscarii sunt date de expresiile:
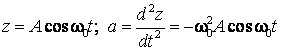(7.5)
Inlocuind
acceleratia din (7.5) in (7.2) si (7.4) si tinand cont de faptul ca perturbatiile
electromagnetice se propaga in vid cu viteza finita 
, vom lua in
(7.4) si (7.5) intensitatile campului electric si magnetic ale undei in punctul
M la un moment , in
functie de acceleratia particulei la momentul 
:
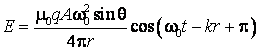(7.6)
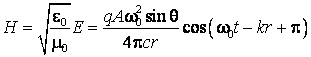(7.7)
Diferenta de faza 
apare datorita semnului negativ al
acceleratiei.
Ajungem
astfel la concluzia ca un purtator de sarcina electrica care efectueaza o
miscare oscilatorie constituie o sursa de unde electromagnetice sferice.
Expresiile (7.6) si (7.7) reprezinta ecuatiile unei unde electromagnetice,
fiind analoage cu ecuatia undei elastice sferice. Din (7.6) si (7.7) rezulta ca
in spatiul liber, lipsit de surse de unde electromagnetice (densitatile de
sarcina electrica si de curent nule), vectorii si ce se propaga prin spatiu satisfac o ecuatie
difererentiala asemanatoare ca forma cu ecuatia undelor elastice:
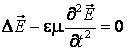(7.8)
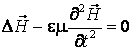(7.9)
Ecuatiile (7.8) si (7.9) sunt valabile pentru medii dielectrice, in care absorbtia undelor electromagnetice este slaba. Prin analogie cu ecuatia undelor mecanice, viteza de propagare a campului electric si magnetic al unei unde electromagnetice este data de relatia:
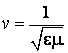(7.10)
De aici tragem concluzia ca atat campul electric, cat si cel magnetic nu sunt localizate in spatiu, propagandu-se cu aceeasi viteza sub forma unor unde. La fel ca la undele mecanice, viteza data de (7.10) este viteza de faza. Propagarea simultana a celor doua campuri prin spatiu reprezinta o unda electromagnetica.
Pentru
medii dielectrice cu permitivitatea 
si permeabilitatea 
viteza de faza a unei unde electromagnetice
are expresia:
(7.10')
In vid, valoarea vitezei de faza pentru o unda electromagnetica este:
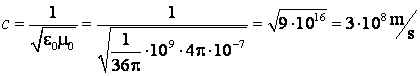
Viteza de propagare a undelor electromagnetice intr-un mediu oarecare se poate scrie sub forma:
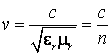(7.11)
unde
este indicele de refractie al mediului fata de
vid. Pentru medii
dielectrice 
si 
.
Egalitatea
(7.12)
se verifica experimental numai la frecvente joase, cand
masuratorile pentru valoarea lui 
se pot face cu metode electrice obisnuite.
Relatia (7.12) nu se mai verifica insa la frecvente inalte, ca de exemplu in
domeniul undele optice. De exemplu, in cazul apei 
, in timp
ce 
. Aceasta neconcordanta
se datoreaza fenomenului de dispersie,
care inseamna dependenta de frecventa a indicelui de refractie, si deci a
permitivitatii relative, la frecvente inalte ale undelor electromagnetice.
Una dintre
solutiile importante ale ecuatiilor diferentiale (7.8) si (7.9) o constituie
unda electromagnetica plana. Daca se alege axa Oz pe directia de propagare a
undei electromagnetice plane, vectorii si vor depinde numai de variabilele 
si sub forma reala:
(7.13)
(7.14)
sau sub forma complexa
(7.15)
(7.16)
In cazul in care unda electromagnetica plana se propaga pe o directie oarecare, ultimele relatii se scriu, conform cu (7.13) si (7.14):
(7.17)
(7.18)
Proprietatile generale ale undelor electromagnetice sunt:
1) Transversalitatea:
(7.19)
2) Vectorii si sunt perpendiculari intre ei:
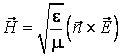(7.20)
unde este versorul directiei de propagare a undei.
3) Vibratiile vectorilor si sunt in faza.
Din (7.20) rezulta ca
intre modulele vectorilor si exista relatia:
(7.21)
Astfel, marimile 
si 
ating concomitent si in aceleasi puncte
valorile maxime, si respectiv cele minime, osciland in faza.
4) Intensitatea undei
electromagnetice plane este proportionala cu patratul amplitudinii vectorului :
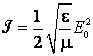(7.22)
|
