RADIATIA TERMICA DE ECHILIBRU

RADIATIA TERMICA DE ECHILIBRU

Experienta arata ca orice corp la temperatura mai mare ca zero absolut emite energie sub forma de radiatie electromagnetica . Radiatia emisa este caracterizata de un spectru continuu , dar distributia spectrala depinde de temperatura corpului emitator . La temperaturi joase (sub 500⁰C), cea mai mare parte a energiei emise este concentrata pe lungimi de unda corespunzatoare radiatiei infrarosii . Odata c 616j93g u cresterea temperaturii , o parte tot mai mare a energiei emise se deplaseaza catre lungimi de unda mici . De exemplu, la temperaturi intre 500^0C si 600⁰C , corpul devine incandescent , emisia avand loc preponderent in spectrul vizibil , iar la 3.000⁰C corpul devine "alb fierbinte".

Cand radiatia cade pe suprafata unui corp, o parte este reflectata, iar o parte este absorbita . De exemplu , corpurile intunecate absorb cea mai mare parte a radiatiei incidente, in timp ce corpurile deschise la culoare reflecta mai mult . Se defineste coeficientul de absorbtie spectrala al unei suprafete An ca fiind fractiunea din energia incidenta pe suprafata , cu frecventa n , care este absorbita de suprafata respectiva . Prin urmare , daca un corp este in echilibru termic cu mediul (T=ct), el trebuie sa emita si sa absoarba aceeasi cantitate de energie in unitatea de timp . Radiatia emisa sau absorbita in aceste conditii se numeste radiatie termica de echilibru . Corpul negru este corpul care absoarbe total orice radiatie incidenta :

An=1 pentru orice n

Radiatia corpului negru are proprietati "universale "si, de aceea prezinta un interes aparte . Astfel ,Kirchhoff a demonstrat , folosind argumente termodinamice generale ca radiatia corpului negru este omogena, izotropa, nu depinde de natura chimica a peretilor cavitatii emitatoare si nici de forma geometrica a acesteia .

Daca r este densitatea volumica de energie a unui corp negru ,

r=aT ⁴  (1)

unde a = 7,64*10^-16 J/m³K⁴ .

Relatia gasita experimental de Stefan in 1779 si dedusa teoretic de Boltzmann in 1884 cu ajutorul principiilor termodinamicii , este cunoscuta sub numele de legea Stefan-Boltzmann.

Sa studiem acum distributia spectrala a radiatiei corpului negru . Notam cu r n,T) densitatea spectrala de energie, asa incat r n,T)dn va fi energia emisa in unitatea de volum a corpului negru aflat la temperatura T , corespunzatoare radiatiei cu frecvente cuprinse intre n si n+dn . Densitatea volumica de energie r(T) este integrala lui r n,T) peste toate frecventele

r(T) =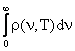

Folosind argumente termodinamice Wien a demonstrat ca functia r n,T) este de forma

r n,T)= n f( (3)

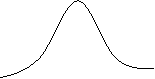
Functia f din legea lui Wien (3) nu poate fi determinata din termodinamica , ci trebuie dedusa din experienta sau din consideratii statistice . Primele masuratori precise ale functiei r n,T) au fost efectuate in 1899 si au aratat ca izotermele (curbele date de ecuatia  (3) la T=constant) pornesc din zero , au un maxim pentru o anumita valuare a lui n , apoi scad si tind la zero cand  n

r n T

nmax

n

Figura 1

Experimental s-a gasit ca =constant  (4)

In fizica experimentala este convenabil sa se lucreze cu densitate spectrala de energie in scara lungimilor de unda r l,T). 

Din conditia r n,T)dn r l,T)dl rezulta

r l,T)=r n,T) r n,T) (5)

Si curba r l,T) la T=constant prezinta un maxim asa incat

l_maxT=b (6)

Constanta b se numeste constanta de deplasare Wien si are valoarea b=2,898 10²mk.

Formulele (4) si (6),care arata cum variaza maximul densitatii spectrale de energie atunci cand variaza temperatura, se numesc legile de deplasare ale lui Wien.

Pentru a determina functia f - si deci r n,T) - trebuie depasit rationamentul termodinamic . Rayleigh si Jeans au dedus o functie de distributie spectrala .

Din teoria electromagnetica rezulta ca radiatia termica dintr-o cavitate trebuie sa existe sub forma de unde electromagnetice stationare . Se poate arata ca numarul acestor unde  -deci numarul de moduri de oscilatie ale campului electromagnetic din cavitate- pe unitatea de volum , cu frecvente cuprinse in intervalul (n n+dn) este

dn =8pdn (7)

Daca <E> este energia medie a modului de oscilatie cu frecventa n , functia de distributie spectrala este produsul dintre nn si <E>

r n,T)= 8p <E> (8)

Conform teoriei Rayleigh-Jeans , undele stationare sunt generate de atomii din peretii cavitatii , care emit si absorb radiatia , comportandu-se ca niste oscilatori armonici cu frecventa n. Energia E afiecarui oscilator clasic poate lua orice valoare intre 0 si , asa incat din mecanica clasica rezulta

<E> =EdP(E)  (9)

dP(E) =c e dE  (10)

<E> ==kT  (11)

Rezultatul este in concordanta cu legea clasica a echipartatiei energiei : oscilatorii armonici contribuie la energia medie cu datorita energiei lor cinetice si cu datorita energiei lor potentiale .

Introducand valuarea (11) a lui <E> in (8) rezulta legea de distributie spectrala Rayleigh-Jeans

r n,T)= 8pkT (12)

La limita frecventelor mici, legea Rayleigh-Jeans (12) aproximeaza valorile experimentale ca in figura 2.

Figura 2

Totusi  r n,T) nu prezinta un maxim si este divergenta pentru n . In plus, formula (12) nu este in acord cu legea Stefan-Boltzmann. Intr-adevar, calculand

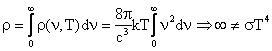
Acest rezultat a fost numit de Ehrenfest "catastrofa ultravioleta".