Relatia relativista dintre masa si energie
Din formula fundamentala a dinamicii relativiste pentru componenta a 4-a
(4.115)
obtinem:
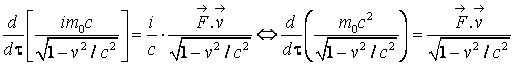(4.116)
de unde
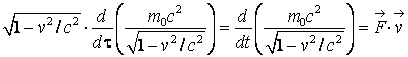(4.117)
Produsul
scalar 
(puterea = variatia energiei
particulei in unitatea de timp):
(4.118)
Asadar, avem :
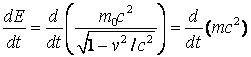(4.119)
sau
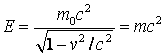(4.120)
Am ajuns
astfel la relatia relativista dintre masa si
energie. Daca 
, din (4.120)
obtinem:
(4.121)
care reprezinta energia de repaus a particulei.
Energia cinetica este diferenta dintre energia totala si energia de repaus:
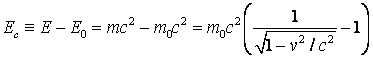(4.122)
Dezvoltarea in serie dupa formula binomului lui Newton ne conduce la expresia:
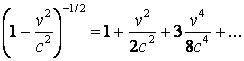
de unde, inlocuind in (3.122), obtinem:
Daca 
ajungem la expresia clasica
(4.123)
Se poate stabili in mod simplu
criteriul de miscare relativista
pentru o particula cu masa de repaus 
, functie
de raportul dintre energia de repaus 
si energia primita sub forma unui lucrul
mecanic 
. Scriind
teorema energiei cinetice, utilizand definitia (4.122) a energiei cinetice
relativiste:
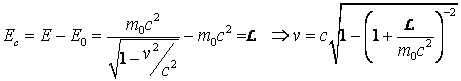
se pot observa doua cazuri:
1) 
, viteza
particulei va fi relativista 
, caz in
care trebuie folosita formula relativista a energiei cinetice pentru calculul
vitezei corpului;
2) 
, viteza va
fi nerelativista 
, caz in
care se poate folosi cu buna aproximatie formula clasica (4.114) a
energiei cinetice pentru calculul
vitezei corpului.
|
