SCARI DE MASURARE - Scari pentru masurari directe

SCaRI DE MaSURARE

1. Formularea problemei

In esenta, masurarea consta in atribuirea de simboluri (cel mai adesea numere) proprietatilor care constituie obiectul masurarii, in conformitate cu o procedura bine stabilita. In atribuirea acestor simboluri se urmareste ca relatiile dintre simboluri sa reflecte in mod adecvat relatiile empirice corespunzatoare proprietatii masurate. Deoarece aceste relatii se stabilesc pe multitudinea de manifestari ale proprietatii masurate, rezolvarea problemei se face cu ajutorul teoriei multimilor, [42].

Notand cu Q multimea manifestarilor individuale ale unei proprietati q si cu i multimea obiectelor W carora le sunt asociate, ansamblul:

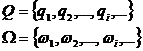(1.7)

reprezinta clasa obiectelor supuse masurarii proprietatii q, facand abstractie de celelalte proprietati ale obiectelor in cauza.

Considerand ca pe multimea Q se poate stabili multimea de relatii empirice:

L , (1.8)

proprietatea q poate fi reprezentata prin sistemul de relatii empirice:

L = < Q, L > .  (1.9)

In mod asemanator se poate considera sistemul de relatii numerice al simbolurilor:

R = < R, P > , (1.10)

unde R este multimea numerelor reale sau o submultime a acesteia, iar P este multimea relatiilor de acelasi tip cu L (n are) definite pe R, adica:

(1.11)

Cu aceste precizari si tinand seama de conditia de reprezentare, ca prin masurare sa se stabileasca o corespondenta intre manifestarile q_i I Q si numerele n_iIR, de o maniera in care relatiile empirice intre elementele q_i sa implice relatiile intre imaginile lor n_i, masurarea se poate defini formal ca fiind operatia empirica obiectiva descrisa de aplicatia:

(1.12)

unde M este un homomorfism al sistemului cu relatii empirice L = < Q, L > in sistemul cu relatii numerice R = < R, P >.

Aceasta inseamna ca pentru l_i I L si p_i I P

(1.13)

adica exista o transformare bijectiva astfel incat

(1.14)

Homomorfismul M sau, mai complet, quadruplul:

S = < L, R, M, F > , (1.15)

defineste ceea ce se numeste o scara de masurare.

Imaginile multimii Q in multimea R prin acest homomorfism, M(q_i) = n_i, reprezinta numere atribuite manifestarilor individuale q_i ale proprietatii q, adica reprezinta valorile marimii masurate q_i pe scara S. Valorile n_i ale marimii masurate sunt dependente de scara S in sensul ca aceeasi marime masurata q_i va avea valori distincte pe doua scari diferite. Avand insa in vedere ca scarile de masurare au structuri asemanatoare ele indeplinind aceleasi conditii de reprezentare, rezulta ca se pot formula relatii de trecere de la valorile obtinute pe o scara la valori exprimate in alta scara, ceea ce in esenta atesta unicitatea masurarii.

2. Scari pentru masurari directe

Masurarile directe sunt acele masurari care se bazeaza exclusiv pe relatii existente intre marimile apartinand aceleiasi clase cu marimea ce se masoara si deci nu necesita masurari de marimi din diverse clase. Masurarile de acest fel sunt cele mai uzuale si se aplica unor marimi precum lungimea, masa, tensiunea electrica s.a. Scarile pentru astfel de masurari depind de sistemul cu relatii empirice corespunzator marimii de masurat, respectiv de tipul si numarul de relatii empirice care pot fi stabilite.

Scari nominale. Cel mai simplu sistem de relatii contine o singura relatie, cea de echivalenta ~, fiind de forma < Q, ~ >. Relatia de echivalenta empirica trebuie sa satisfaca axiomele de simetrie, tranzitivitate si de reflexibilitate [42].

Intre un sistem < Q, ~ > si un sistem cu relatii numerice < R, = > exista intotdeauna un homomorfism. Scara de masurare stabilita pe aceasta cale se numeste scara de masurare nominala deoarece valorile pe care le determina nominalizeaza clasa de echivalenta pe multimea Q.

Pentru construirea unei scari nominale se alege un set de obiecte cu proprietati caracteristice pentru marimea de masurat, dar diferite sub aspectul criteriului de echivalenta, set care formeaza o submultime de etaloane:

(1.16)

unde e_iI Q, i = 1,2, , n si e_i~ e_j numai daca i = j.

Elementele e_i determina clase de echivalenta pe Q si fiecaruia dintre ele i se atribuie arbitrar un numar (simbol) n_i cu singura conditie ca n_i n_j daca i j

Masurarea consta in compararea, printr-o metoda corespunzatoare relatiei de echivalenta empirica, a obiectului care manifesta marimea de masurat q_x cu elementele setului de etaloane. Daca in set se gaseste un etalon e_x astfel incat e_x ~ q_x atunci marimea q_x se exprima prin numarul n_x atribuit etalonului respectiv. In acest fel nu pot fi determinate decat atatea valori cate etaloane distincte contine setul de etaloane si pot exista marimi q_x I Q care sa nu aiba etaloane echivalente.

Ca exemplu de scara nominala poate fi dat codul culorilor stabilit prin atribuirea de numere unui set de obiecte avand culori diferite. Acest cod nu furnizeaza nici un fel de informatie despre culori, iar in urma masurarii se poate sti daca culoarea de masurat are un echivalent in setul de culori sau nu.

Valorile obtinute pe o scara nominala nu permit punerea in evidenta a vreunei semnificatii intre marimile de masurat si nici efectuarea de operatii algebrice cu numerele reprezentand scara respectiva. De aici rezulta o utilizare restransa a acestui tip de scara care de altfel, in acceptiunea moderna a notiunii de scara, nu este considerata o scara de masurare, ci mai degraba un mijloc de a identifica anumite forme de manifestare a unor proprietati.

Scari ordinale. Daca intr-un sistem cu relatii empirice, in afara de relatia de echivalenta exista si o relatie de ordine ' < ' , reflexiva, tranzitiva si antisimetrica [42] sistemul devine <Q, ~ ,< >. Existenta homomorfismului care se aplica la acest sistem in sistemul cu relatii numerice corespunzator < R, = , < > a fost demonstrata de Cantor [26]. Daca prin '<' se exprima o relatie de ordine simpla, homomorfismul este un izomorfism, iar scara de masurare se numeste scara ordinala sau scara de ordine.

Ca si in cazul relatiei de echivalenta trebuie elaborat si un procedeu experimental de comparare pentru a se pune in evidenta si relatia de ordine '<'.

Pentru realizarea unei scari ordinale se alege un set de etaloane care formeaza submultimea E = , avand insa elementele aranjate in ordinea determinata de <Q, ~ , < > adica e₁ < e₂ < ,, < e_n. Acestor etaloane li se atribuie numere, astfel incat ordinea lor sa corespunda cu ordinea din E.

Masurarea consta, de asemenea, in compararea marimii de masurat q_x cu etaloanele din E. Daca se gaseste q_x ~ e_x rezulta valoarea n_x pe scara respectiva. Daca nu se poate stabili o relatie de echivalenta cu nici un etalon se pot stabili doua etaloane consecutive intre care se situeaza q_x adica e_i < q_x < e_i+1 si astfel se deduce ca marimea q_x are o valoare n_i < n_x < n_i+1, ceea ce constituie un plus de informatie fata de scara nominala.

Cele mai uzuale scari ordinale sunt scarile pentru masurarea duritatii mineralelor si a metalelor, cele pentru masurarea intensitatii cutremurelor, cele pentru masurarea tariei vantului s.a. Astfel, scara Mohs pentru duritate are ca etaloane 10 minerale in ordinea crescanda a duritatii (talc, gips, calcit, fluorina, apatita, ortoza, cuart, topaz, corindon, diamant) si in aceasta ordine li s-au atribuit numerele naturale de la 1 la 10. Pentru cutremure exista in mod uzual scara Richter cu 9 grade si scara Mercali cu 12 grade de magnitudine, iar pentru taria vantului exista scara Beaufort cu 12 grade magnitudine, de la lipsa de vant la uragan.

Numerele atribuite in cadrul scarilor ordinale sunt arbitrare, singura conditie care trebuie respectata este conditia de ordonare. Din aceasta cauza nu se pot stabili relatii cantitative sau de raport intre numerele scarii, iar cu astfel de numere nu pot fi realizate operatii aritmetice.

Finetea masurarii poate fi marita marind numarul de etaloane dar aceasta complica procedura de masurare iar problema se rezolva printr-un compromis.

Scari de raport. Limitarile specifice scarilor nominale si ordinale au condus la necesitatea definirii unor sisteme care, pe langa relatiile binare de echivalenta si ordonare formate din dubletii q_i, q_j I Q, sa contina si o relatie ternara _* care implica tripletii q_{i *} q_j ~ q_l pentru q_i, q_j I Q, rezultand q_l I Q. Sistemul ternar astfel obtinut se noteaza < Q, ~ , <, _* > .

Relatia ternara _* care reprezinta o operatie binara (cu doi operanzi) este denumita concatenare si se efectueaza in functie de natura marimii de masurat. Astfel, pentru masurarea maselor cu balanta procedura consta in punerea greutatilor pe acelasi taler, pentru masurarea lungimilor procedura consta in asezarea cap la cap a unor tije sau benzi.

Marimile care permit o concatenare de tipul celor descrise mai inainte se numesc marimi extensive, iar concatenarea astfel realizata se numeste concatenare aditiva, deoarece prezinta o asemanare cu adunarea numerelor reale. Nu toate marimile prezinta aceasta proprietate de aditivitate. Astfel, factorul de amplificare pentru doua amplificatoare conectate in serie este egal cu produsul si nu cu suma factorilor de amplificare a celor doua amplificatoare, pe cand densitatea a doua corpuri avand aceeasi densitate este egala cu densitatea acestora si nu cu suma densitatilor.

Proprietatea de aditivitate a marimilor extensive reprezinta un caz particular al marimilor numite intensive definite ca marimi la care concatenarea este indempotenta sau care nu permite o concatenare directa.

In cele ce urmeaza vor fi luate in seama numai marimile extensive si vor fi formulate numai concluziile practice cu privire la construirea si folosirea scarilor de masurare pentru astfel de marimi. Detalii pot fi gasite in [42] , [26].

Pentru construirea unei scari de masurare pentru marimi extensive, care permit concatenarea aditiva, este suficient sa se aleaga un singur etalon a carui marime e₁IQ este adoptata ca referinta. Se adopta un alt element e¹₁~ e₁ care prin concatenare cu e₁ formeaza etalonul e₂ ~ e_{1 *} e₁. Acest etalon e₂ ~ 2e₁. Concatenand noul etalon e₂ cu e¹₁ se obtine e_{2 *} e¹₁ ~ e₃ si astfel se poate obtine un sir de etaloane e₁, e_{2 ,}, e_n in care primul etalon este egal cu unitatea, iar ultimul este e_n = ne₁ = n.

Intr-un mod asemanator se poate obtine un set de n etaloane subunitare adoptand de data aceasta un element e¹_1/n ~ e₁/n care va servi la concatenare. Primul etalon va fi e¹_1/n, al doilea etalon va avea valoarea 2e¹₁/n, al treilea va avea valoarea 3e¹₁/n, iar al n-lea va avea valoarea ne¹₁/n ~ e₁ = 1. In acest mod pot fi construite seturi de etaloane oricat de mari folosind un singur etalon.

Elementul etalon minimal e₁ caruia i se atribuie numarul 1, reprezinta unitatea de masura a scarii. Pe o astfel de scara valoarea numerica pentru q_x rezulta ca raport intre numarul asociat etalonului echivalent e_x si cel atribuit etalonului e₁. Prin urmare, definitia clasica conform careia rezultatul masurarii este dat de raportul dintre marimea de masurat si unitatea de masura este corecta numai in cazul masurarii marimilor extensive care admit concatenarea aditiva.

Datorita caracterului arbitrar al alegerii etalonului e₁ exista posibilitatea definirii de scari cu proprietati similare, dar care pentru aceeasi marime masurata sa exprime valori diferite. Caracteristic pentru valorile obtinute pe doua astfel de scari este faptul ca raportul lor este constant, de aceea scarile pentru marimi extensive care admit concatenarea aditiva se numesc scari de raport.

Cu valorile numerice obtinute prin intermediul scarilor de raport pot fi efectuate operatii corespunzatoare relatiilor de echivalenta si ordonare precum si orice fel de operatii algebrice, ceea ce explica foarte larga utilizare practica a acestor scari.

Scari de interval. Pentru anumite marimi fizice operatia de concatenare nu este posibila decat pe anumite intervale. Ca exemplu poate fi data temperatura, pentru care valorile se exprima numai sub forma unei diferente fata de o referinta arbitrara, careia i se atribuie valoarea zero.

Prin interval se intelege o pereche ordonata (q_i, q_j), q_i, q_j I Q fiind capetele intervalului. Doua intervale (q_i, q_j) si (q_e, q_m) sunt echivalente daca produc aceleasi efecte empirice. Doua intervale (q_i, q_j) si (q_e, q_m) sunt adiacente daca q_j ~ q_e si prin concatenare se obtine intervalul (q_i, q_m).

Pentru construirea unei scari de interval se alege ca etalon un interval (s₀,s_n)IQ cu s₀ < s_n. In cadrul acestui interval se stabilesc n subintervale adiacente echivalente (s_i, s_i+1) ~ (s_j, s_j+1) cu s_i < s_i+1 si s_j < s_j+1 pentru i, j = 1,…, n, prin concatenarea carora rezulta intervalul etalon adoptat: (s₀, s_n) ~ (s₀, s₁) _* (s₁, s₂) _{* *} (s_n-1, s_n) ~ n(s₀, s₁).

Capatului inferior al intervalului s₀ i se atribuie valoarea zero, iar subintervalului (s₀, s₁), ca si celorlalte (n-1) intervale, li se atribuie valoarea 1 care are semnificatia de unitate de masura a scarii. Unei marimi q_x care se incadreaza in intervalul (s₀, q_x) si care contine n_x intervale (s₀, s_i) i se atribuie valoarea n_x.

Valorile numerice determinate prin scarile de interval pot fi folosite in orice fel de operatii algebrice fiind tot atat de uzuale ca si valorile obtinute prin scarile de raport.

Ca exemple de scari de interval pot fi date scarile de temperatura Celsius, Reaumur si Fahrenheit. Scara Celsius este definita pe intervalul etalon determinat de temperatura de topire a ghetii, care marcheaza valoarea zero, si de temperatura de fierbere a apei marcata cu valoarea 100. Scara are deci 100 de intervale echivalente, iar subintervalul unitar este denumit grad Celsius.

Scari pentru masurari indirecte Dupa cum s-a aratat in paragraful 2, masurarea directa a unei proprietati se poate face pe baza relatiilor existente numai in clasa respectiva. Exista insa numeroase marimi care nu pot fi masurate in acest fel. De exemplu, marimi intensive precum randamentul unei masini, viteza unei reactii chimice sau fizice nu pot fi masurate prin metode directe deoarece trebuie sa se apeleze la relatii din mai multe clase de proprietati iar determinarea valorilor acestor marimi se face pe baza relatiilor existente in toate clasele de proprietati.

Masurarile care se efectueaza pe baza mai multor clase de proprietati se numesc masurari indirecte. Construirea de scari pentru asemenea masurari este, evident, mai complicata. In principiu se procedeaza ca si la construirea scarilor pentru masurari directe, dar in plus se tine seama si de relatia care defineste marimea masurata pe baza marimilor masurate direct, relatie care indica modul de combinare a marimilor direct masurabile ca sa rezulte marimea determinata indirect pe aceasta cale.

Tratarea completa a acestei probleme depaseste cadrul acestei lucrari.