STATICA SOLIDULUI RIGID

O bara omogena AB de lungime l si greutate G se sprijina in punctul A pe sol si in C pe un perete vertical (fig.1). Bara este fixata in D printr-un fir inclinat cu un unghi de 30 . Sa se determine tensiunea din fir si reactiunile in punctele A si C.

O bara AB de greutate G si lungime 2l este rezemata cu un capat pe sol si sprijinita in C pe suprafata unei emisfere de raza r. In capatul A al barei este prins un fir, care sustine la extremitatea sa o contragreutate P (fig.2). Sa se determine reactiunile in punctele A, C si unghiul a in pozitia de echilibru.

Fig.2

R. Planul orizontal va introduce reactiunea normala N₁, iar emisfera va aplica in C o forta N₂ perpendiculara pe bara. In raport cu axele reperului Oxy, conditiile de echilibru sunt:

Cum din cele trei ecuatii rezulta

, , .

bara isi pastreaza legaturile daca reactiunea N₁ este reala si pozitiva, deoarece reazemul din A este o legatura unilaterala; rezulta urmatoarele conditii referitoare la lungimea barei

.

Asadar, intr-una din pozitiile de echilibru, lungimea barei nu poate fi oricat de mare caci ar exista pericolul rasturnarii in jurul punctului C atunci cand centrul de greutate nu ar fi situat intre A si C si nici mai mica decat valoarea minima AC.

Sa se determine pozitia de echilibru a corpului format din doi semicilindri de densitate r si raze R si ( fig.3).

Fig.3

R. Asupra rigidului actioneaza greutatile G₁, G₂ si forta normala N de reactiune a planului orizontal. Pozitiile centrelor de greutate vor fi determinate de distantele

Unghiul a se obtine din ecuatia de echilibru a momentelor fortelor fata de C:

unde se introduce ; rezulta .

Ecuatia de proiectie pe axa Oy furnizeaza forta normala de contact a planului

.

Daca cilindrul cel mare are o densitatea neglijabila fata de cea a celuilalt se obtine , iar daca cilindrul cel mic are o greutate neglijabila atunci a

Bara AB de lungime 2l si greutate G, la capatul careia atarna o greutate P, se reazema in A pe un perete si in C pe muchia unui zid (fig.4). Cunoscand distanta a dintre pereti sa se determine reactiunile din reazeme si unghiul a in pozitia de echilibru.

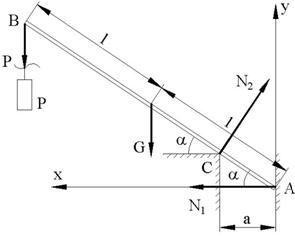
Fig.4

R. Pe langa reactiunile normale N₁ si N_2, se introduc fortele exterioare: greutatea G si tensiunea din fir P. Ecuatiile de proiectie pe Ax si Ay si ecuatia momentelor in A sunt

Din ultima ecuatie de echilibru se obtine

,

iar din celelalte rezulta reactiunile

.

Conditiaeste echivalenta cu. Asadar, echilibrul este posibil daca centrul de greutate al barei este situat intre cei doi pereti.

Se considera sistemul format din bara AB de greutate G, suspendata la capete cu doua fire si o placa metalica de greutate specifica g. Cele doua fire sunt legate de firul CD fixat in D (fig.5). Cunoscand, sa se determine pozitia de echilibru a barei si tensiunile din fire.

R. Bara AB impreuna cu placa metalica formeaza un solid mentinut in repaus sub actiunea fortelor G, g l si a tensiunilor S₁, S₂.

Din ultima ecuatie se obtine

iar din primele rezulta tensiunile din fire

.

Intre doi pereti verticali este introdusa o bara AB de greutate G, care este inclinata cu unghiul a fata de orizontala. Bara este prinsa in C cu un fir vertical, iar in D este suspendata greutatea P (fig.6). Cunoscand distantele a si b ale firelor la cei doi pereti si distanta l dintre acestia, sa se determine fortele din legaturi.

R In punctele A si B se introduc reactiunile normale N_A, N_B, iar in C si D vor actiona tensiunile din fire S, P. Bara fiind omogena, greutatea sa G va fi aplicata la mijlocul ei.

O bara omogena OA de lungime l si greutate G este fixata printr-o articulatie la capatul ei superior O (fig.7). De celalalt capat este prins un fir ce trece peste un scripete B si sustine greutatea P. Stiind ca OA = OB = l, sa se determine reactiunea din articulatie si unghiul de inclinare al barei in pozitia de echilibru.

Fig. 7

R. Asupra barei actioneaza greutatea G, tensiunea din fir P si reactiunea R₀ din articulatie. Notand cu componentele acestei reactiuni, ecuatiile scalare de echilibru sunt:

Din ecuatia de momente rezulta unghiul a la echilibru

In aceasta pozitie de echilibru, componentele reactiunii din articulatie se deduc din primele doua ecuatii:

, .

O bara omogena, de lungime 4a si greutatea G, este fixata prin articulatia A si rezemata in B pe coltul unui zid de latime a. La capatul C al barei este suspendata greutatea P.

Cunoscand AB = 3a, BD = a, sa se calculeze reactiunile in A si B (fig.8).

O bara cotita de greutate neglijabila si de dimensiuni AD = 4a, DE = a este articulata in O si rezemata in B (fig.9). In B actioneaza o forta egala cu 2P iar in A si E fortele P, Q. Cunoscand AO = CD = OB = a, OC = 2a , sa se determine reactiunile din legaturile barei.

R. Pe langa fortele gravitationale mai actioneaza fortele din legaturi: reactiunea normala N in reazemul C si reactiunea din articulatia cilindrica O cu componentele H si V.

Ecuatiile scalare de echilibru sunt urmatoarele:

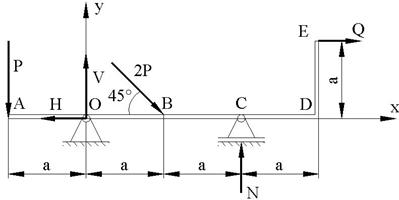
Fig.9

din care rezulta

Un sistem de ecuatii echivalente conduce la aceleasi rezultate. De exemplu, scriind doua ecuatii de momente fata de O, C si o singura ecuatie de proiectie pe Ox, se obtine sistemul

Acest sistem este mai usor de rezolvat, deoarece fiecare ecuatie contine o singura necunoscuta, iar ecuatia de proiectie pe Oy poate fi utilizata pentru verificarea rezultatelor.

O grinda cotita ABC, incastrata in A, este incarcata cu o sarcina concentrata F, doua sarcini distribuite: una uniforma p, iar cealalta triunghiulara de intensitate maxima q si un cuplu de moment M₀ care actioneaza in B (fig.10). Cunoscand AB = l, BC = h, DC = a, sa se determine reactiunea si momentul cuplului din incastrare A.

R. Incastrarea se inlocuieste cu doua forte perpendiculare, si cu un cuplu de moment M_A. In raport cu axele reperului xAy se scriu ecuatiile de echilibru:

Fig.10

de unde se obtine

Pe grinda OAB, formata dintr-o bara orizontala si un arc de cerc, actioneaza o forta concentrata P si inca o forta distribuita de intensitate q (fig.11).

O placa omogena de greutate G, de forma unui semicerc de raza r, este rezemata in punctele A, B, C. Placa este actionata in D cu o forta verticala P (fig.12). Sa se afle reactiunile din legaturi.

R. Asupra placii actioneaza forta P, greutatea G in punctul M situat la distanta si reactiunile normale N_A, N_B, N_C. Deoarece fortele sunt paralele cu axa Bz, ecuatiile de echilibru sunt:

Un paralelipiped de dimensiuni AB = BC = a, DE = 2a si de greutate G este articulat in A, rezemat in B si D si suspendat cu firul HI in prelungirea laturii EH. Fiind supus fortelor , , , , sa se determine reactiunile din A, B, D si tensiunea din firul HI (fig.13).

R. Izoland rigidul, asupra lui actioneaza forte cunoscute si forte din legaturi. Ecuatiile generale de echilibru sunt:

Fig.13

Rezolvand sistemul rezulta:

Bara cotita OABC, incastrata in O, este formata din bara verticala OA = 2l si din trei bare identice AB, BC, DE, perpendiculare intre ele si de aceeasi lungime l (fig.14). Sa se determine reactiunile care apar in incastrarea O.

R. Fortele de legatura din incastrare se reduc la o reactiune (R_x, R_y, R_z) si la un cuplu de moment (M_x, M_y, M_z). Ecuatiile de echilibru pentru sistemul spatial de forte si cupluri de forte sunt:

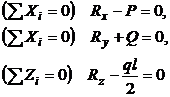
Fig.14

de unde rezulta