Semnale modulate

Semnale modulate

4.1.Utilizarea semnalelor modulate

Semnalele purtatoare de informatie nu indeplinesc intotdeauna conditiile optime de propagare prin mediul de legatura intre emitator si receptor. Ca urmare se procedeaza la o transferare a caracteristicilor (parametrilor) semnalului care contine informatia asupra unui alt semnal. Acest proces este numit modulatie (modulare) si se realizeaza la emisie. La receptie se efectueaza transformarea inversa, numita demodulatie (demodulare).

Prin modulatie se urmareste:

Imbunatatirea propagarii prin mediul de legatura intre emisie si receptie

Multiplicarea cailor prin diviziune in fercventa

Imbunatatirea stabilitatii la perturbatii prin cresterea raportului semnal/ perturbatie

Vom numi:

Semnalul care contine informatie (mesajul) se va numi semnal modulator si se noteaza cu s(t)

Semnalul asupra caruia se transfera informatia se va numi semnal purtator si se noteaza cu P(t)

Clasificarea metodelor de modulatie se poate face dupa mai multe criterii. Este foarte util, pentru o tratare sistematizata, sa clasificam modulatiile dupa natura semnalului puratator:

(1)Modulatie cu purtator sinusoidal

(2)Modulatie cu purator in impulsuri

Modulatia cu purtator sinusoidal se poate realiza prin transferarea caracteristicilor mesajului asupra amplitudinii, asupra frecventei sau asupra fazei semanului purtator. Se obtin, corespunzator:

1.Modulatia de amplitudine (MA)

2.Modulatia de frecventa (MF)

3.Modulatia de de faza (MP sau M

Observand ca un semnal purtator sinusoidal (cosinusoidal) poate fi reprezentat analitic sub forma:

(2.211)

sau sub forma (echivalenta):

(2.212)

modulatia in amplitudine este o modulatie liniara, iar modulatiile de frecventa si de faza sunt modulatii exponentiale.

Modulatia cu purtator in impulsuri implica utilizarea unui semnal purtator format din impulsuri dreptunghiulare periodice, cu posibilitatea de modificare a ur 717f59h matorilor parametri: amplitudinea impulsurilor, frecventa acestora, pozitia impulsurilor pe (axa de timp) sau durata impulsurilor. Rezulta corespunzator:

1.Modulatia impulsurilor in amplitudine (MIA)

2.Modulatia impulsurilor in frecventa (MIF)

3.Modulatia impulsurilor in pozitie (MIP)

4.Modulatia impulsurilor in durata (MID)

Sa observam ca modulatiile cu purtator sinusoidal permit multiplexarea si diviziunea cailor in frecventa, iar modulatiile cu purtator in impulsuri permit multiplexarea si diviziunea cailor in timp.

4.2.Modulatia cu purtator sinusoidal

Considerand un semnal purtator de forma (4.1), alegerea functiei sinus sau cosinus se poate face numai dupa criteriul obtinerii unor relatii matematice cat mai simple, daca faza initiala nu este semnificativa in tratarea problemei de modulatie asa cum este cazul in continuare.

Pentru o tratare analitica cat mai unitara si concisa, sa consideram succesiv modulatia liniara si modulatia exponentiala.

4.2.1.Modulatia liniara.

S-a aratat ca modulatia de amplitudine (MA) este o modulatie liniara si implica transferarea parametrilor semnalului modulator asupra amplitudinii semnalului purtator .

Fie un semnal purtator de forma (2.211) sau (2.212)

si un semnal modulator .

In modulatia de amplitudine, amplitudinea purtatorului devine:

(2.213)

sau, uneori,

(2.214)

Se obtine - pentru cazul (2.213) - expresia semnalului MA de forma:

()

Consideram trei cazuri pentru exemplificare:

Caz I: (2.216)

Semnalul (2.215) devine:

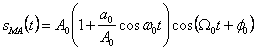(2.217)

Introducand notatia:

(2.218)

parametrul m, numit grad de modulatie, are o semnificatie fizica sugestiva, ????? marimea relativa a variatiei de amplitudine a semnalului MA. Intr-adevar daca se noteaza deviatia de amplitudine a semnalului , din (4.7) se observa ca:

(2.219)

Inlocuind (2.218) in (2.217), rezulta:

(2.220)

Exemplificarea analitica obtinuta cu de forma (2.216) este ilustrata grafic in Fig 4.1, in care s-au reprezentat: semnalul purtator (Fig 4.1a), semnalul modulator (Fig 4.1b) si semnalul MA (Fig 4.1c).

Curba reprezentata cu linie intrerupta in Fig 4.1c este numita infasuratoare.

Pentru a exista posibilitatea de reconstituire a semnalului la receptie este necesar sa fi indeplinite conditiile:

(2.211)

(2.212)

Intr-un mare numar de aplicatii practive, (sau, in procente, ).

Sa observam ca din Fig 4.1c rezulta, tinand seama si de relatia (2.219):

(2.223)

si

(2.224)

adica

(2.225)

Relatiile (2.223) si (2.224) se mai pot scrie:

(2.226)

(2.227)

de unde

(2.228)

Gradul de modulatie m poate fi determinat experimental, prin vizualizarea semnalului MA, masurand si utilizand relatiile (2.225) sau (2.228).

Pornind de la expresia (2.220) a semnalului , putem scrie:

(2.229)

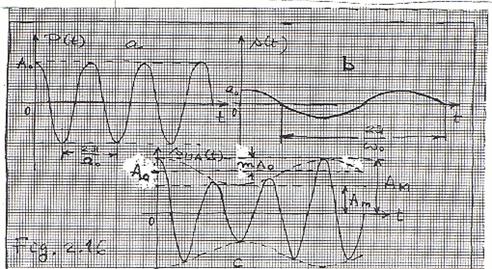
Ultima expresie evidentiind componentele spectrale ale semnalului modulat si constituind o dezvoltare in serie Fourier a acestui semnal (modulat in amplitudine). In Fig 2.17 s-au reprezentat spectrele de amplitudini ale purtatorului (Fig 2.17a), ale mesajului (Fig 2.17b) si ale semnalului MA (Fig 2.17c).

Din Fig 2.17c se observa ca spectrul de amplitudini al semnalului MA contine o componenta centrala (de amplitudine si de frecventa ) care este chiar purtatoarea si doua componente laterale (de amplitudini si decalate cu fata de purtatoare). Componenta de frecventa mai este numita componenta laterala superioara.

Banda de frecventa a semnalului MA este:

(2.230)

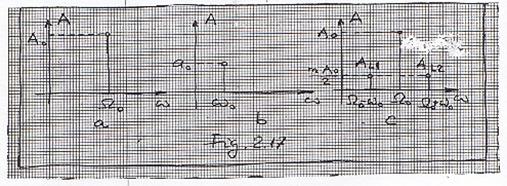
Se poate face si o reprezentare a semnalului MA sub forma de diagrama vectoriala Fig 2.18.

Intr-adevar, presupunand planul reprezentarii fix, vectorul de amplitudine care se roteste cu viteza unghiulara , corespunde purtatoarei primului termen din (2.229). In aceeasi figura Fig 2.18, vectorii de amplitudini si cu vitezele unghiulare si fata de plan, respectiv cu vitezele unghiulare si fata de vectorul , corespund termenilor doi si trei din expresia (2.229) a semnalului MA.

Cand rezultatele vectorilor mici se suprapun peste vectorul , rezulta sau , dupa cum rezultanta are acelasi sens cu sau, respectiv, are sens opus sensului pe care il are .

In aceeasi reprezentare, se poate considera ca vectorul este fix si ca planul vectorial se roteste cu viteza unghiulara . Vectorii mici se vor roti cu vitezele unghiulare in jurul vectorului mare.

Aplicatiilor practice le sunt specifice semnalele modulatoarecu structuri complexe. Daca aceste semnale sunt periodice sau pot fi reprezentate printr-un semnal periodic, ele pot fi puse sub forma:

(2.231)

Inlocuind (2.231) in (2.215), se obtine:

(2.232)

unde

(2.233)

este gradul de modulatie al componentei de ordin k a mesajului (2.231).

Expresia 2.232 se poate scrie

(2.234)

Conditiile (2.221) si (2.222) devin respectiv

(2.235)

si

(2.236)

cu .

In Fig 2.19 s-a exemplificat un spectru de amplitudini al unui semnal MA (Fig 2.19b), pentru un mesaj cu spectrul de amplitudini ca in Fig 2.19a (k=3).

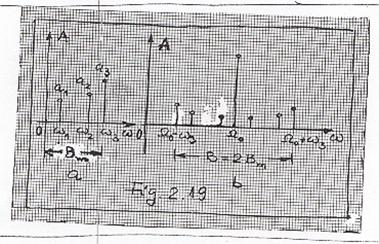
Semnalul MA contine deci purtatoarea si doua benzi laterale. Notand cu banda mesajului, banda semnalului MA este:

(2.237)

In cazul mesajelor neperiodice, fie s(t) un astfel de semnal care admite transformata Fourier si sa notam cu S(w) aceasta transformata.

Semnalul MA va avea expresia:

(2.238)

dupa cum rezulta din relatia (2.215), pentru , tinand seama ca putem pune mesajul s(t) sub forma:

(2.239)

Purtatorul fiind de durata infinita, transformata Fourier a semnalului MA se va obtine trecand la limita in transformata Laplace. O rezolvare a acestei probleme este data in /3/. Acelasi rezultat se poate obtine si printr-o rezolvare formala, pe alta cale, prezentata in continuare.

Tinand seama de precizarile facute, relatia (2.238) se poate pune sub forma:

(2.240)

Functia de densitate spectrala (transformata Fourier) a semnalului (2.240) este:

(2.241)

si se obtine aplicand transformarea (2.241) semnalului si tinand seama de teorema deplasarii:

(2.242)

Rezulta:

(2.243)

Primii doi termeni din expresia (2.243) se obtin considerand in relatia (2.242) - in locul functiei s(t) - functia constanta si tinand seama ca:

(2.244)

si, in baza teoremei simetriei,

(2.245)

Si in relatia (2.245), teorema simetriei s-a aplicat dupa trecerea la limita.

Intr-adevar, considerand F(w) definit prin:

(2.246)

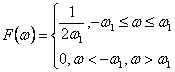
daca F(w) este transformata Fourier inversa a functiei f(t),

(2.247)

Din relatiile (2.246) si (2.247) se obtine succesiv relatiile:

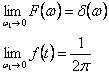
ceea ce justifica de fapt relatia (2.245).

Ilustrare grafica a relatiei (2.243) este prezentata in Fig 2.20.

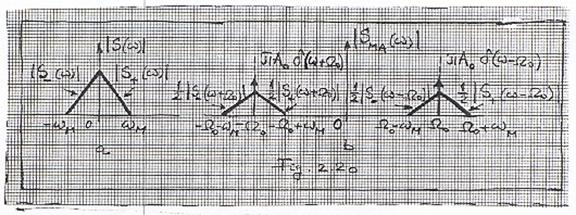Astfel daca se cunosc spectrul mesajului (Fig 2.20a) si purtatoarea, rezulta usor spectrul semnalului MA - dupa regula reprezentata analitic prin relatia (2.243) si reprezentata grafic in Fig 2.20b. Componentele apar datorita faptului ca purtatorul are durata infinita. Interpretarea fizica a frecventelor negative a fost facuta in subcapitolul 2.3.1.

Relatia (2.215) poate fi reprezentata prin modelul analogic prezentat in Fig 2.21 (pentru )

Intr-adevar, daca unui dispozitiv de inmultire I se aplica la o intrare functia A(t) - (2.213) - iar la cealalta intrare functia , la iesire se obtine semnalul , conform relatiei (2.215) - cu .

Daca

(2.248) A(t)=s(t)

caz frecvent utilizat in practica, relatia (2.215) devine

(2.249)

Dezvoltand expresia (2.249) si comparand cu (2.229), se va constata ca in aceasta expresie nu exista semnalul purtator. Din acest motiv, modulatia de tipul (2.249) se numeste modulatie de amplitudine de produs sau modulatie de amplitudine cu purtatoare suprimata.

4.2.2.Modulatia in amplitudine (MA):

Transpunerea informatiei binare in semnale MA

Operatori pentru semnale MA

Domeniul timp

Domeniul frecventa

1.Domeniul timp:

Mesajul

pentru MA cu ambele benzi laterale si cu purtatoare

MA cu purtatoare suprimata (modulatie de produs)

si s(t) exista MA cu ambele benzi laterale, dar cu purtatoare redusa.

2.Domeniul frecventa:

Mesajul 

unde

Legatura intre operatorii si :

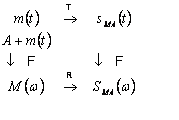
Calculul lui :

Calculul functiei :

nu sunt indeplinite conditiile de aplicabilitate a transformatei Fourier.

indicele de crestere al functiei M(p)

este olomorfa in semilanul , unde indicele de crestere al functiei G(p).

unde P(q) este integrandul si

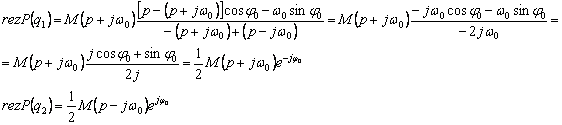
Calculul functiei :

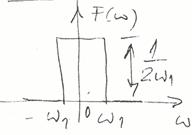
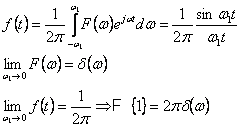
Sau:

Sau:

Cu conditia sa se considere transformatele Fourier prin trecere la limita.

In aplicatiile practice, transformarea semnalelor MA se realizeaza prin mai multe metode:

1.Semnalele MA cu purtatoare si ambele benzi laterale (P+2BL)

Metoda permite reconstituirea simpla a mesajului la receptie, prin detectia anvelopei semnalului MA, dar necesita o banda larga (), conform relatiei (2.237) si o putere mare la emisie (puterea purtatoarei si puterea benzilor laterale).

Aceasta modulatie se utilizeaza in radiodifuziune, pentru ca permite scheme simple de detectie in radioreceptoare.

2.Semnale MA cu purtatoare suprimata (2BL)

Aceasta modulatie rezulta prin MA de produs. Semnalele necesita aceeasi banda ca in cazul anterior, in schimb scade sensibil puterea necesara la emisie. La receptie, detectia este mai complicata, deoarece este necesara refacerea purtatoarei.

Metoda este avantajoasa atunci cand banda disponibila este suficient de mare (nu este necesara multiplicarea cailor in frecventa), iar puterea disponibila la emisie nu este mare.

3.Semnale MA cu banda laterala unica (BLU)

Aceste semnale se obtin trecand semnale P+2BL prin filtre care retin numai o singura banda laterala (eliminand purtatoarea si a doua banda laterala). Avantajele metodei constau in reducerea benzii de frecvente si in reducerea puterii la emisie. Metoda este recomandata pentru multiplicarea eficienta a cailor in frecventa, insa prezinta dezavantajul posibilitatilor complicate de detectie.

In unele aplicatii se utilizeaza o banda laterala cu purtatoare redusa, caz in care detectia se face in conditii mai usoare comparativ cu situatia cand purtatoarea este complet suprimata.

Modulatia exponentiala

Considerand semnalul purtator sinusoidal sub forma (2.211) sau (2.212), putem scrie:

(2.250)

(2.251)

reprezinta faza semnalului la un moment dat si se numeste faza instantanee.

Frecventa semnalului se poate defini ca fiind viteza de variatie a fazei, adica

(2.252)

Functia (2.252) este numita frecventa instantanee a semnalului.

Daca frecventa instantanee (2.252) este data, faza instantanee se obtine prin integrare:

(2.253)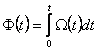

Pentru valori constante ale functiei W(t), de exemplu pentru semnale sinusoidale:

(2.254)

si din (2.253) se obtine (2.251), se poate interpreta ca o constanta de integrare.

Notand cu s(t) semnalul modulator, in modulatia exponentiala, caracteristicile acestuia se transfera asupra functiei .

Pentru modulatia de faza MP (M ), modificarea fazei se exprima prin:

(2.255)

iar in modulatia de frecventa MF se intervine asupra frecventei instantanee, corespunzatoare relatiei:

(2.256)

Deci, in modulatia exponentiala se opereaza asupra fazei instantanee a semnalului, direct asupra acestuia in modulatia de faza (2.255) sau prin interiorul frecventei instantanee, in modulatia de frecventa (2.256).

4.2.3.Modulatia de frecventa (MF):

Fie semnalul purtator:

(2.257)

si semnalul modulator:

(2.258)

Modulatia de frecventa implica modificarea frecventei instantanee corespunzator relatiei (2.256):

(2.259)

unde s-a notat

(2.260)

Marimea este numita deviatie de frecventa a semnalului MF.

Faza instantanee se obtine prin integrarea frecventei instantanee, conform relatiei (2.253):

(2.261)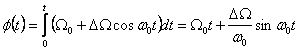

Se noteaza cu b marimea

(2.262)

care reprezinta derivata relativa de frecventa si care este numita indice de modulatie de frcventa.

Semnalul MF rezulta inlocuind (2.261) in (2.257), cu notatia (2.262):

(2.262)

Ultima relatie se mai scrie:

(2.263)

Termenii din (2.263) se exprima prin functii Bessel, tinand seama ca:

(2.264)

(2.265)

unde este functia Bessel de speta intai, de ordin n si de argument x.

Reamintim ca ecuatia:

cu n real sau complex, se numeste ecuatia lui Bessel, iar solutiile acestei ecuatii sunt functii Bessel.

Sa dezvoltam relatia (2.236), dupa relatiile (2.264) si (2.265):

(2.266)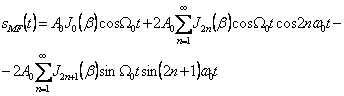

Produsele din (2.266) se pot dezvolta in continuare:

(2.267)

Relatia ultima se poate scrie mai condensat, notand

2.268 2n=k

2.269

Functiile Bessel de speta intai cu prorietatile:

(2.270) pentru k par

(2.271) pentru k impar

Ca urmare, expresia (2.269) devine

(2.272)

Semnalul MF este format din purtatoare si doua benzi laterale, fiecare cu un numar infinit de componente, simetrice in raport cu purtatoarea de frecventa . Componentele benzilor laterale sunt amplasate la intervale (de frecventa ...

Lipseste pg 141 (287)

Ecuatia transcedenta (2.275) are solutia (aproximativa):

(2.276)

Banda semnalului MF (cu doua benzi laterale) va fi in consecinta:

(2.277)

dupa cum rezulta din (2.269) sau (2.272) si tinand seama de (2.276), rezulta

(2.278)

Pentru valori mici ale indicelui de modulatie b, din (2.278) se observa ca daca

(2.279)

(2.280)

adica o banda echivalenta cu cea ocupata de semnalul MA - (2.230).

In acest caz, din 2.269 se obtine

(2.281)

adica o purtatoare si doua componente laterale (ca in cazul semnalului MA), dar cu amplitudini diferite fata de semnalul MA si cu cele doua componente laterale defazate (cu p

Daca

(2.282)

din (2.278) rezulta, tinand seama de (2.282):

adica

(2.283)

Relatia 2.283 evidentiaza un fenomen foarte important pentru aplicatiile practice si anume faptul ca pentru valori mari ale marimii b - conform conditiei (2.282) - banda efectiva a semnalului modulator (adica de frecventa mesajului).

Ca urmare, semnalele MF au b mare se utilizeaza in radio difuziune deoarece fiind bine protejate fata de perturbatii si permit transmiterea unui spectru audio larg (practic intraga banda audio).

Semnalele MF cu b mic - relatia (2.279) - sunt utilizate in telefonie si telegrafie, deoarece necesita o banda mica si sunt protejate le perturbatii intr-o masura suficienta, ca urmare a transmiterii prin circuite cu fire.

In cazul unui mesaj (semnal purtator) cu structura complexa, fie

(2.284)

expresia acestuia, aceeasi ca (2.231) si rezultand, de asemenea, daca mesajul este periodic sau poate fi reprezentat printr-un semnal periodic.

Rezulta corespunzator relatiilor (2.250), (2.256), (2.253) si (2.261):

(2.285)

unde

(2.286)

Expresia (2.285) se poate scrie:

(2.287)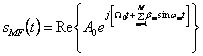

daca

(2.288)

Dar

(2.289)

si inlocuind in 2.287, putem scrie:

(2.290)

Din analiza expresiei (2.290) se poate observa ca spectrul obtinut este extrem de complex, el continand armonicele frecventelor modulatoare (m=1,2,.,M) precum si toate combinatiile posibile de forma:

(2.291)

unde pot fi orice numere intregi. O componenta oarecare din (2.290) are amplitudinea:

(2.292)

si este amplasata la ecartul

(2.293)

in raport cu purtatoarea de frecventa .

Se poate considera prin analogie cu (2.276) ca cele mai mari valori ale indicilor din (2.292) sunt:

(2.294)

si pentru valori mai mari decat cele din (2.294), componentele respective se pot neglija.

Cu totul aproximativ, prin analogie cu (2.277) , (2.278) si (2.283) se poate considera ca banda semnalului (2.290) este

(2.295)

adica banda B este aproximativ egala cu suma benzilor obtinute daca s-ar modula purtatoarea, succesiv, cu componentele ale mesajului (2.284).

Daca frecventele sunt frecvente armonice, spectrul se determina prin dezvoltari in serie Fourier - /7/.

4.2.4.Modulatia de faza (MP sau M

In modulatia de faza, relatia intre mesaj si purtatoare este (2.255).

Fie mesajul

(2.296)

care, inlocuit in (2.255), da faza instantanee

(2.297)

Notand

(2.298)

marimea reprezinta deviatia de faza a semnalului modulat.

Pentru un purtator (2.257)

,

rezulta semnalul MP

(2.299)

Alegand

(2.300)

si notand

(2.301)

se observa ca (2.299) este relatia (2.262), in care b s-a inlocuit cu a

Marimea a este numita indice de modulatie de faza.

Urmand aceeasi cale ca in cazul semnalelor MF, se obtine:

(2.302)

sau, mai restrans,

(2.302)

Pentru banda de frecvente se obtine, la fel ca in cazul semnalelor MF,

(2.304)

Daca

(2.305)

(2.306)

iar pentru

(2.307)

(2.308)

Pentru a mic, rezulta de asemenea, un spectru similar semnalelor MA.

Observand ca in timp ce indicele b este o derivatie de frecventa relativa (2.262), indicele este o derivatie de faza neraportata - (2.301) - care nu depinde de frecventa mesajului.

Ca urmare, din (2.308) rezulta ca pentru valor mari ale lui a, banda efectiva a semnalelor MP depinde de frecventa mesajului.

Aceasta este o deosebire esentiala intre modulatiile MP si MF si din acest punct de vedere, modulatia de faza este mai putin avantajoasa decat modulatia de frecventa.

Semnalele MP se utilizeaza mult in transmisiunile de date (in impulsuri), deoarece asigura o protectie sporita fata de perturbatii.

4.3.Modulatia cu purtator in impulsuri

4.3.1.Modulatia impulsurilor

Modulatia impulsurilor presupune un semnal purtator format din impulsuri.

S-au evidentiat, de asemenea, patru modalitati de realizare a modulatiei impulsurilor: MIA, MID, MIP si MIF.

Sa observam ca modulatia impulsurilor in pozitie (MIP) afecteaza faza purtatorului, fiind deci o modulatie de faza (MI ). Cum si  modulatia in frecventa (MIF) modifica tot faza (ca urmare a modificarii frecventei instantanee) rezulta ca se pot trata modulatiile MI si MIF ca fiind modulatii MIP (precizand-se daca modulatia pozitiei se face prin intermediul fazei initiale sau prin intermediul frecventei instantanee).

Ca urmare, in literatura de specialitate se prezinta trei tipuri de modulatii in impulsuri:

Modulatia impulsurilor in amplitudine (MIA)

Modulatia impulsurilor in faza (MIP)

Modulatia impulsurilor in distanta (MID)

4.3.2.Modulatia impulsurilor in amplitudine (MIA)

Modulatia impulsurilor in amplitudine este ilustrata in Fig 2.21. Purtatorul P(t)  este reprezentat in Fig 2.21a, mesajul s(t) este cel din Fig 2.21b, iar semnalul MIA, sub forma s(t)P(t), este prezentat in Fig 2.21c.

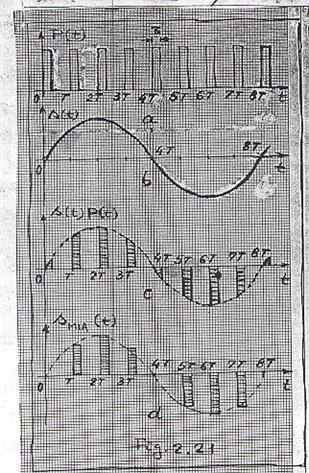
In Fig 2.22 s-a indicat modalitatea de obtinere a semnalului respectiv (Fig 2.21c), care este rezultatul unei modulatii de amplitudine de produs. Se mai observa ca acelasi semnal - s(t)P(t) - reprezinta o esantionare a mesajului s(t) cu purtatorul P(t).

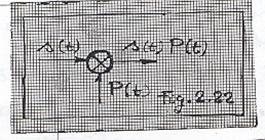
In practica obtinerii semnalelor MIA, este mai avantajos (pentru simplificarea gradului de complexitate a echipamentelor utilizate) sa se obtina semnalul din Fig 2.21d (in locul semnalului din Fig 2.21c).

Semnalul - Fig 2.21d - se poate obtine cu circuite logice care furnizeazaacest semnal format din impulsuri de amplitudini s(kT) si de durate t

Studiul semnalelor astfel obtinute este totusi dificil.

Pentru simplificarea studiului analitic, se procedeaza in modul urmator:

se inlocuieste semnalul din Fig 2.21d, cu semnalul din Fig 2.23c, semnalul rezultat prin esantionarea aceluiasi mesaj s(t) - Fig 2.23b - dar cu un purtator P(t) translatat pe axa timpului cu (Fig 2.23a) in raport cu diagrama din Fig 2.21a.

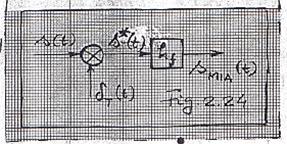
se considera semnalul - Fig 2.23c - ca fiind obtinut prin procesul indicat in Fig 2.24, unde este circuitul de formare care permite obtinerea acestui semnal din semnalul esantionat - Fig 2.23d.

Procesul indicat justifica translatarea purtatorului P(t) cu - pentru a detine amplitudinile impulsurilor care formeaza semnalul egale cu amplitudinile impulsurilor care compun semnalul , la momentele kT - Fig 2.23.

In continuare sa determinam functia de densitate spectrala

(2.3090

si forma analitica a semnalului .

Din Fig 2.24 se observa ca

(2.310)

unde

(2.311)

si

(2.312)

Sa calculam deci functiile si .

Pentru prima functie, pornind de la relatia (2.311), sa inlocuim

(2.313)

Se obtine

(2.314)

adica

(2.315)

In relatiile 2.314 s-a inlocuit prin

conform rezultatului (2.36).

In ceea ce priveste relatia (2.315), s-a tinut seama ca:

si

,

in conformitate cu rezultatele din paragraful 2.31.

De asemenea, sa mai mentionam ca intre T si W (2.315) exista relatia .

Determinarea functiei se face pornind de la forma functiei - Fig 2.25 - si aplicand (2.312):

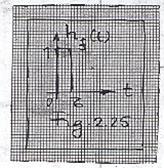
(2.316)

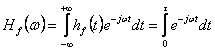
adica, dupa efectuarea integralei din (2.316),

(2.317)

Inlocuind acum (2.315) si (2.317) in (2.310), rezulta:

(2.318)

Transformata Fourier (2.318) permite reducerea expresiei analitice a semnalului .

Intr-adevar, in baza relatiei (2.310), conform proprietatilor produsului de convolutie, putem scrie:

(2.319)

Pe de alta parte insa, s-a stabilit (2.177) si (2.178) ca produsul (2.313) se poate scrie mai simplu sub forma:

(2.320)

Inlocuind (2.320) in (2.319), obtinem succesiv:

(2.321)

Deoarece ultima integrala din (2.321) reprezinta convolutia functie cu functia , rezulta:

(2.322)

Spectrul de amplitudini al semnalului (2.322), adica modululu transformatei Fourier (2.318) a fost reprezentat in Fig 2.26b, pentru S(w) avand alura din Fig 2.26a.

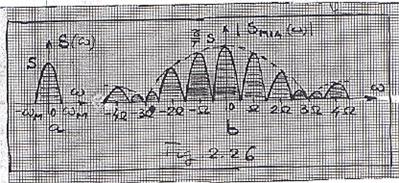
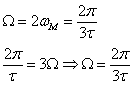
Se observa ca esantionarea cu P(t) format din simboluri de durata finita produce distorsionarea spectrului de amplitudini al semnalului. Distorsionarea aceasta este numita si efect de apertura si este cu atat mai pronuntata cu cat t este mai mare (in banda de baza a semnalului - Fig 2.26).

La limita, pentru , din (2.317) se observa ca:

si in acest caz dispare efectul de apertura.

La aplicatiile practice se respecta conditiile:

(2.323)

cu t convenabil de mic, astfel incat sa nu apara dificultati in realizarea generatoarelor impulsurilor P(t), iar efectul de apertura sa fie acceptabil.

Modulatia impulsurilor in amplitudine se utilizeaza ca procedeu de baza in multiplexarea cailor de telecomunicatii in timp - /19/.

4.3.3.Modulatia impulsurilor in pozitie (MIP)

Dupa cum s-a aratat, in cazul MIP, parametrul care se modifica este pozitia impulsurilor semnalului P(t), modificarea rezultand prin schimbarea fazei initiale a semnalului sau prin modificarea frecventei instantanee.

Principiul modulatiei a fost ilustrat in Fig 2.27, cu purtatorul P(t) - Fig 2.27a, mesjul s(t) - Fig 2.27b si semnalul MIP, - Fig 2.27c.

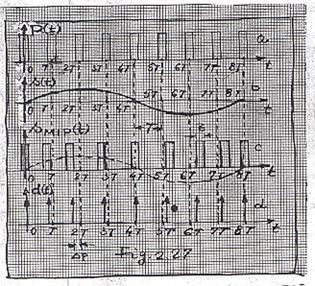
Deplasarea fata de pozitia normala este DP si corespunde amplitudinii maxime a mesajului. Astfel, pentru t=2T, impulsul de durata t corespunzator este deplasat cu Dp la stanga, iar pentru t=6T, deplasarea cu Dp se face spre dreapta (Fig 2.27c).

Daca purtatorul este , rezulta semnalul MIP idealizat d(t) - Fig 2.27d.

Apare evidenta conditia:

(2.324)

necesara pentru ca impulsurile sa nu alunece unele peste altele.

Studiul analitic al semnalelor MIP se poate face in mod analog studiului semnalelor MIA, considerand insa diagrama din Fig 2.28.

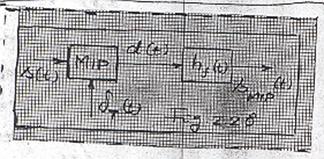
Astfel, semnalul se obtine din semnalul d(t) - Fig 2.27d - cu circuitul de formare a carui functie este aceeasi ca in cazul semnalelor MIA - Fig 2.24 si Fig 2.25.

Spectrul semnalelor MIP este mult mai bogat decat in cazul semnalelor MIA, componentele acestui spectru exprimand-se prin functia:

(2.325)

care contine functii Bessel ale caror argument depinde de Dp.

Semnalele MIP se utilizeaza in transmisiunile de date, deoarece ofera o protectie sporita fata de perturbatii - /19/.

4.3.4.Modulatia impulsurilor in durata (MID)

In aceasta modulatie, mesajul s(t) modifica durata t a impulsurilor purtatorului - Fig 2.29.

Se observa ca pentru valori pozitive s(kT), duratele impulsurilor sunt mai mari decat t, iar pentru valori negative s(kT), aceste durate sunt mai mici decat t, in ambele cazuri proportionale cu amplitudinile s(kT).

Semnalele MID se pot obtine realizand in prealabil o modulatie de tipul MIP si utilizand apoi operatiile de insumare si integrare - /5/.

Spectrul acestor semnale este foarte larg.

Tipul de semnale MID se utilizeaza mai putin in transmisiunile de informatii, dar isi gasesc o mare aplicabilitate in aparatura de masura si control.