Spatiul Minkowski. Cuadrivectori

Spatiul Minkowski. Cuadrivectori

Matematicianul Minkowski a propus, in anul 1908, spatiul cu patru dimensiuni, in care pe langa cele trei coordonate spatiale:

(4.62)

se introduce a patra coordonata

(4.63)

In acest continuum "spatiu-timp', intervalul dintre doua evenimente se scrie sub forma :

(4.64)

analog cu distanta dintre doua puncte in spatiul fizic tridimensi­onal:

(4.65)

Marimea este invarianta in raport cu transformarile Lorentz, la fel cum este invarianta in raport cu transformarile Galilei. Invarianta intervalului inseamna ca daca un even 141c25b iment are loc in sistemul de referinta intr-un punct de coordonate , iar in raport cu sistemul de referinta se desfasoara in punctul de coordonate , atunci:

Invarianta intervalului (4.64) arata legatura indestructibi­la dintre spatiu si timp. In concordanta cu conceptiile materialismului dialectic, teoria relativitatii scoate in evidenta faptul ca spatiul si timpul, ca forme de existenta a materiei, nu pot fi privite independent unul de altul. Izolarea notiunilor de spatiu si timp ne conduce la spatiul absolut si timpul absolut, care sunt notiuni aproximative, valabile numai la viteze relative mult mai mici decit viteza luminii in vid.

Se verifica simplu ca utilizand notatiile (4.62) si (4.63), transformarile Lorentz (4.34) si (4.35), devin:

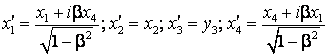(4.67)

respectiv

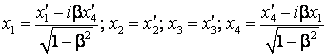(4.68)

unde s-a utilizat notatia obisnuita

(4.69)

Transformarile Lorentz (4.67) si (4.68) pot fi interpretate ca o rotatie a axelor cu unghiul , astfel ca axele si sa ramina in repaus (fig.12). Proiectiile pe axele si ale unui punct sunt:

iar pe axele si sunt:

Prin aceasta rotatie transformari­le de coordonate sunt:

(4.70)

Comparind formulele (4.67) si (4.68) obtinem:

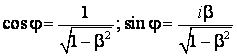
Asadar, transformarile Lorentz pot fi interpretate in spa­tiul cuadridimensional ca o rotatie a sistemului de coordonate si cu unghiul , astfel ca:

 

Unui eveniment fizic in spatiul tridimensional ii corespunde, la un moment dat, un punct in spatiul cuadridimensional, numit punct de uni­vers. Evolutia acestui eveniment in timp si spatiu reprezinta o linie de univers. Semnificand distanta intre doua puncte ale liniei de univers, poate fi privit ca un cuadrivector cu componentele Un cuadrivector (sau mai simplu 4 - vector) repre­zinta ansamblul a patru marimi, care sunt componentele vectorului , si care prin trecerea de la un referential inertial la altul se trans­forma la fel cu coordonatele si , vezi (4.67) si (4.68):

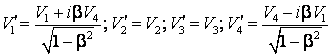, (4.73)

respectiv:

(4.74)

Se poate arata simplu, prin calcul direct, ca lungimea unui cuadrivector, precum si produsul scalar a doi cuadrivectori, sunt marimi invariante fata de transformarile Lorentz.

Transformarile Lorentz (4.73) si (4.74) pot fi scrise si in alta forma, utilizand elementele de matrice:

(4.75)

(4.76)

unde ia valorile 1, 2, 3, 4, iar pe indicele care se repeta se sumeaza de la 1 la 4.

Matricea transformarii directe este:

(4.77)

iar matricea transformarii inverse este:

(4.78)

Prin calcule directe obtinem: 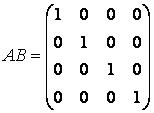(4.79)

Deoarece cvuadrivectorii sunt invarianti in raport cu transforma­rile Lorentz, pentru invarianta relativista a legilor fizice se im­pune scrierea lor in forma cuadrivectoriala.

Notiunea de timp introdusa in TRR implica modificari esentiale pentru succesiunea in timp a evenimente­lor. Astfel, pentru doua evenimente si exista doua posi­bilitati:

(4.80)

In acest caz se spune ca evenimentele se afla unul fata de altul in pozitie de tip temporal. In cazul

(4.81)

se spune ca evenimentele se afla unul fata de celalalt in pozitie de tip spatial.

Succesiunea evenimentelor de tip temporal este aceeasi in ra­port cu orice sistem de referinta inertial, in timp ce succesiunea evenimentelor de tip spatial depinde de sistemul de referinta iner­tial.

In fig.13 evenimentul are loc in originea sistemului de co­ordonate. Orice eveniment din conul de lumina (domeniul hasurat) se poate afla in po­zitie de tip temporal fata de evenimen­tul , si toate evenimentele din afara conului se afla in ra­port cu evenimentul in pozitie de tip spatial.

Limita dintre cele doua domenii este fenomenul de propagare a luminii. Daca un eveniment este cauza celuilalt, succesiunea lor in timp trebuie sa fie aceeasi in raport cu orice observator, ceea ce inseamna ca poate exista o legatura cauzala numai intre acele evenimente care se afla unul fata de celalalt in pozitie de tip temporal. In ipoteza ca evenimentul ce are loc in originea co­ordonatelor este cauza, iar evenimentul este efectul, atunci evenimentul se poate afla numai in partea dirijata in sus a conului de lumina, asa numitul "con inainte'. Evenimentul poate fi efectul al carei cauza este evenimentul numai daca se afla in partea dirijata in jos a conului de lumina, adica in "conul inapoi".

Liniile de univers pentru procesele cauzale trebuie sa se afle in interiorul conului de lumina, ceea ce reprezinta propagarea interactiilor cu viteza .

Teoria relativitatii restrinse permite impartirea continuumului spatiu-timp in trecut, prezent si viitor (fig.13).

Viitorul pentru evenimentul , ce are loc in originea sistemului de coordonate, il reprezinta totalitatea evenimen­telor care pot fi influentate cauzal de evenimentul , adica evenimentele cuprinse in "conul inainte'. Trecutul pentru evenimen­tul il reprezinta totalitatea evenimente­lor care l-au putut influenta pe , adica ansamblul evenimentelor din "conul inapoi'. Prezentul il constituie ansamblul evenimentelor asupra carora evenimentul nu poate influenta si nici nu poate fi influentat de ele.

Exemplul 6

Sa se demonstreze ca distanta intre doua puncte este invarianta la transformarile Galilei, iar intervalul este invariant in raport cu transformarile Lorentz.

Rezolvare

La geometrie se arata ca distanta intre doua puncte cu razele vectoare , respectiv intr-un sistem inertial este

Distanta dintre aceleasi doua puncte, masurata in alt sistem inertial (fig.1), este

Din transformarile Galilei (4.5) obtinem:

de unde se obtine:

Fata de sistemul de referinta din fig.8, intervalul dintre doua evenimente este (4.64):

Intervalul dintre aceleasi doua evenimente fata de sistemul de referinta este:

Din transformarile Lorentz (4.34) obtinem:

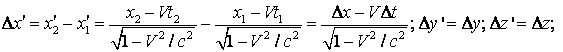
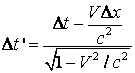
Inlocuind si in expresia lui , dupa calcule simple obtinem: