Starea de polarizare a undelor electromagnetice
S-a aratat ca un dipol
electric oscilant 
emite in toate directiile
unde electromagnetice, care se propaga in sensul razei vectoare 
. Este specific faptul ca
vectorul 
vibreaza tot timpul in planul
format de vectorii si , iar vectorul 
vibreaza perpendicular pe acelasi plan (fig.5).
Planul in care vibreaza
vectorul 
se numeste plan de vibratie, iar planul in care vibreaza vectorul 
se numeste plan de polarizare (fig.4). Acestea sunt denumiri adoptate istoric
prin consens, nereprezentand nici un sens fizic. Unda reprezentata in fig.6 se numeste unda plan
polarizata, sau liniar polarizata.
Subliniem ca transversabilitatea undelor luminoase si polarizarea
acestora au fost descoperite cu mult inainte de teoria electromagnetica a
luminii, insa pana la aparitia teoriei electromagnetice a luminii putine
aspecte erau elucidate. Astfel, polarizarea luminii solare produsa de atmosfera
este folosita din vrem 121e49b uri imemoriale de catre pasarile migratoare pentru a se
orienta in calatoriile lor lungi fata de pozitia Soarelui, atunci cand acesta
este la amurg sau rasarit, ori pe cer innorat. Vikingii foloseau inca acum 1200
ani un compas ceresc in calatoriile lor prin Marea Nordului sau Oceanul
Atlantic piatra solara in incursiunile lor pe continentul american. Intre 860
si 1010 ei au colonizat Islanda, ajungand pana in nordul continentului
american. Desi compasul magnetic a fost descoperit in 1200, vikingii reuseau sa
se orienteze pe ce noros, sau cand Soarele era la asfintit sau rasarit,
folosind "piatra solara". Aceasta a fost descoperita in nordul Europei, si
consta dintr-un conglomerat de mci cristale montate intr-un tub ingust, ce
constituia un polariscop adecvat pentru observarea polarizarii cerului.
Deoarece asupra sarcinilor
electrice ale mediului in care se propaga unda electromagnetica actioneaza in
principal vectorul intensitate a campului electric 
, rezulta ca experimental
este mai usor de detectat planul de vibratie al vectorului , decat planul de
polarizare.
Consideram o unda electromagnetica care se propaga in
sensul axei 
, cu
vectorul intensitate a campului electric cuprins intr-un plan paralel cu planul
(fig.7). Acest vector poate fi descompus in
fiecare moment in doua componente, dupa axele 
si 
:
Se stie ca orice unda transversala este echivalenta cu doua unde liniar
polarizate in plane perpendiculare intre ele, avand aceeasi pulsatie, dar fiind
defazate cu 
. Pentru simplificare
consideram vibratia vectorului in planul 
. Din (7.49) rezulta
ca in acest plan componentele vectorului pe axele si sunt :
Traiectoria descrisa de
varful vectorului 
, in planul se obtine prin compunerea oscilatiilor
perpendiculare, fiind data de relatia :
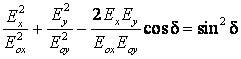
S-a obtinut astfel ecuatia unei elipse pentru care axele si nu sunt axele principale decat in cazuri
particulare. Unda electromagnetica pentru care proiectia varfului vectorului in planul perpendicular pe directia de
propagare a undei descrie o elipsa, se numeste unda polarizata eliptic.
Ne vom ocupa de cateva cazuri particulare.
a) Daca 
din ecuatia (7.51) se obtine:
(
Se poate observa ca in acest caz unda electromagnetica este liniar
polarizata, directia de polarizare fiind cuprinsa in cadranele 1-3. Vectorul ramane tot timpul paralel cu axa 
, care face
unghiul 
cu axa (fig.8 a), astfel incat:
(7.53)
b) Daca 
, avem:
(7.54)
In acest caz unda electromagnetica este de asemenea liniar polarizata, insa directia de polarizare se afla in cadranele 2 si 4 (fig.8 b).
Pentru o directie oarecare de propagare o unda plana liniar polarizata se scrie sub forma :
unde 
este o amplitudine reala, constanta.
a) Daca 
, (7.51) devine:
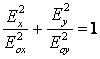(7.56)
si obtinem ecuatia unei elipse pentru care si sunt axe principale (fig.9).
Este simplu de vazut ca pentru
varful vectorului se deplaseaza pe elipsa in sensul acelor de
ceasornic, iar daca 
in sens invers. In functie de sensul de rotatie
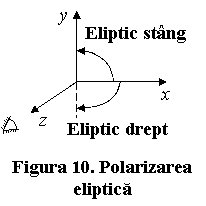
al varfului vectorului lumina este polarizata eliptic drept (la rotatia in sensul miscarii acelor ceasornicului,
in jurul normalei la frontul de unde - axa pentru unda plana), sau eliptic stang (la rotatia in sens contrar - fig.10. Daca 
, lumina este circular polarizata (pe dreapta sau pe stanga).
Pana aici ne-am ocupat de unda elecromagnetica emisa de o
sursa de unde elementara. In cazul surselor obisnuite de lumina insa,
inregistram unde electromagnetice - sau mai corect spus - pachete de unda provenind simultan de la un numar extrem de mare de
surse elementare. Fiecare atom poate fi privit, din punct de vedere al
electrodinamicii clasice, ca un dipol electric oscilant, care emite un pachet
de unde. In fiecare pachet de unde generat de un dipol electric oscilant
vectorul vibreaza paralel cu axa
dipolului, si deci unda respectiva este plan polarizata.
O sursa obisnuita de unde,
ca de exemplu filamentul unui bec, contine un numar foarte mare de dipoli
oscilanti, ale caror axe sunt orientate izotrop in spatiu. Astfel, unda
electromagnetica generata de o sursa monocromatica este de fapt o suprapunere
de pachete de unde, iar in fiecare pachet de unde, vectorul vibreaza paralel cu axa dipolului care l-a
generat. Daca axele dipolilor din sursa sunt orientate cu aceeasi probabilitate
pe orice directie, atunci si suma proiectiilor vectorului 
ce caracterizeaza fiecare pachet de unde, va
fi aceeasi pe orice directie.
In scopul intelegerii
modului de introducere a gradului de
polarizare pentru o unda electromagnetica, presupunem ca radiatia se
propaga perpendicular pe planul hartiei, si dispunem de un "instrument" care
inregistreaza intensitatea undei electromagnetice numai in cazul cand vectorul vibreaza pe o anumita directie.
Daca prin rotirea "instrumentului" acesta inregistreaza aceeasi intensitate a
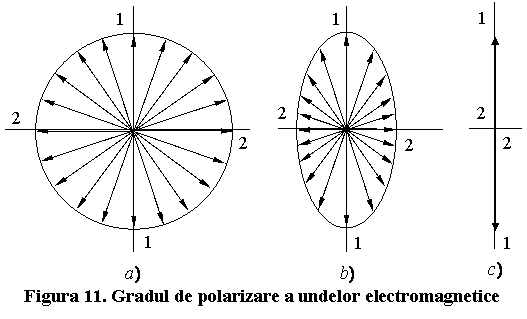
undei, se poate afirma ca toate directiile de vibratie ale vectorului sunt echivalente, si atunci unda este naturala
sau nepolarizata (fig.11 a).
Exista situatii cand
intensitatea undei inregistrate de " instrument" nu este aceeasi pentru orice directie (fig.11
b). O astfel de radiatie se numeste partial
polarizata. In figura (fig.11 b) se observa ca intensitatea 
inregistrata de "instrument" , cand acesta
este orientat in directia 1-1, este mai mare decat intensitatea 
inregistrata pe directia 2-2. Daca 
, iar 
(fig.11 c), radiatia este liniar
(sau plan) polarizata.
Marimea 
definita prin relatia:
(7.57)
se numeste gradul de polarizare
al luminii. Daca 
lumina este naturala (nepolarizata), pentru 
lumina este liniar polarizata, iar pentru 
lumina este partial polarizata.
Exemplul 2
Sa se arate ca o unda plana
transversala ale carei componente 
si 
sunt unde armonice plane care se propaga in lungul
axei Oz:
si 
este polarizata eliptic.
Rezolvare
Consideram partea reala a
expresiilor functiilor de unda si :
si eliminam timpul intre cele doua expresii, de unde obtinem o ecuatie identica cu (2.86) de la compunerea oscilatiilor perpendiculare:
Varful vectorului obtinut prin compunerea celor doua oscilatii care se propaga in directia Oz va descrie o elipsa intr-un plan perpendicular pe axa Oz.
|
