Statica punctului material

Statica punctului material

Statica punctului material liber (fara legaturi)

Discutie:

Evident, tratarea oricarui tip de miscare mecanica sub actiunea unor forte aplicate (directe) si fara frecare corespunde ca modelare matematica interactiunii mecanice mediata de campuri de forte: de exemplu, in acest mod poate fi modelata matematic miscarea (clasica a) unui electron in camp electric sau magnetic, ori c 111c21b aderea unei pietre in camp gravitational etc. Asadar, consideratiile ce se vor face in analiza interactiunilor mecanice fara frecare nu sunt simple „exercitii matematice” (cazuri ideale); ele modeleaza matematic situatii reale in limitele permise de anumite aproximatii.

Orice sistem de forte care actioneaza asupra unui punct material nu poate fi decat concurent si anume in punctul ce modeleaza acest sistem mecanic simplificat. Ori, conform unor consideratii anterioare, torsorul unui astfel de sitem este echivalent cu o forta.

In ceea ce priveste statica punctului material liber, consecinta imediata a acestui fapt este aceea ca sistemul ecuatiilor de echilibru se reduce la anularea rezultantei fortelor directe aplicate:

cu toate consecintele ce decurg de aici (se particularizeaza banal discutia generala).

O situatie mai deosebita este aceea a punctului material supus actiunii unui camp de forte (rezultant) potential, in care expresia analitica a rezultantei fortelor aplicate este de tipul . In acest caz, tinand cont de definitia diferentialei, conditia de echilibru se transforma echivalent:

Prin urmare, in punctul de echilibru E potentialul U are un punct stationar: energia potentiala admite un extrem absolut sau relativ. Analiza diferentialei de ordinul al II-lea in aceste puncte ne conduce, pe baza interpretarii geometrice a acesteia, la considerarea a trei stari distincte de echilibru:

U admite un minim in E: stare de echilibru stabil

E este punct de inflexiune: stare de echilibru indiferent

U admite un maxim in E : stare de echilibru instabil

Denumirile celor trei tipuri de echilibre nu sunt intamplatoare. Analiza cinematica a scoaterii punctului material din aceasta stare (deplasarea sa din E in E’ foarte apropiat) ne arata ca:

daca E este punct de echilibru stabil, punctul material va ramane in apropierea sa, efectuand mici oscilatii de o parte si de alta a acestei pozitii;

daca E este punct de echilibru indiferent, scoaterea sa din aceasta stare conduce fie la o noua stare de echilibru, fie la o departare constanta si lenta de E;

daca E este punct de echilibru instabil, atunci scoaterea punctului material din aceasta stare conduce la departarea sa rapida („exponentiala”) de aceasta pozitie.

Statica punctului material supus la legaturi

Particularizarea sistemului general de echilibru la cazul de fata conduce la relatiile urmatoare:

Vom considera in continuare situatiile elementare de legaturi fara frecare la care poate fi supus punctul material (orice alta situatie este o suprapunere a acestora):

a) echilibrul p.m. rezemat pe o supratata

Sa presupunem ca punctul material este obligat sa ramina permanent pe o suprafata neteda, fixa (in reperul ales) si nedeformabila S, data de ecuatia carteziana implicita (modelul matematic al acesteia creat de geometria diferentiala)

Considerand punctul P(x, y, z) ca punctul de echilibru al punctului material si notand cu (P) planul tangent in P la S, conform modelului matematic al fortelor de legatura in situatia contactului mecanic direct, rezulta ca sistemul fortelor de legatura ce actioneaza asupra punctului material din partea suprafetei S se reduc doar la reactiunea normala, (normala in P la S si avand sensul opus sensului miscarii posibile, interzisa de suprafata), deci .

Dar geometria diferentiala ne arata ca aceeasi directie, normala in P la S, o are si gradientul lui f in punctul P; rezulta de aici ca vom avea:

Cu acestea, conditiile de echilibru se scriu

Discutii:

Prima relatie vectoriala are o consecinta imediata: pentru ca punctul material sa fie in echilibru, trebuie ca rezultanta fortelor directe aplicate sa fie normala in punctul de echilibru, P, la suprafata de sprijin (indreptata in sens opus reactiunii normale), deci:

In situatia considerata este posibil sa eliminam parametrul l si obtinem trei relatii ce dau numai starea de echilibru (nu si normala):

Ecuatia suprafetei poate fi data si sub alte doua forme echivalente, in care avem urmatoarele consideratii:

forma carteziana explicita:

Notand avem acelesi consideratii, dar pentru aceasta relatie de legatura implicita.

- forma carteziana parametrica: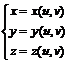

In acest caz derivatele partiale ale lui f se inlocuiesc cu jacobienii corespunzatori:

b) echilibrul p.m. rezemat pe o curba neteda

Consideram aici o alta situatie elementara in care punctul material este obligat sa ramana permanent pe curba neteda C, modelata matematic prin sistemul de ecuatii implicite carteziene

Aceste ecuatii le putem considera ca ecuatiile carteziene a doua suprafete S₁ si S₂, a caror intersectie este C: problema pusa revine deci la a obliga punctul material sa ramana simultan pe cele doua suprafete. Sunt valabile astfel consideratiile anterioare, cu considerarea a doua reactiuni normale date de relatiile:

3. Statica p.m. supus la legaturi cu frecare

a) echilibrul p.m. rezemat pe o suprafata aspra (cu frecare)

Fie un punct material obligat sa ramana pe suprafata S modelata matematic prin ecuatia carteziana explicita

si rezultanta fortelorce actioneaza asupra acestuia.

Cu notatiile din figura 29 si conform celor discutate la fortele de frecare, sistemul ecuatiilor de echilibru se scrie in acest caz dupa cum urmeaza (apare, in plus, conditia de nealunecare pe suprafata):

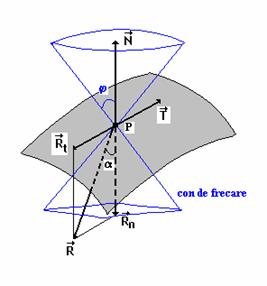
Fig. 29

Discutii:

Daca inlocuim coeficientul de frecare cu si inlocuim in conditia de nealunecare componentele reactiunii cu cele ale rezultantei, obtinem imediat conditia de nealunecare sub forma unghiulara:

Aceasta arata ca echilibrul punctului material este realizat daca si numai daca rezultanta fortelor directe „ramane” in asa-numitul con de frecare reprezentat in figura anterioara (axa coincide cu normala la suprafata in punctul P, iar generatoarea face cu aceasta unghiul j

Sub o forma unica, indiferent de valoarea lui a, relatiile anterioare se scriu:

Aceasta, impreuna cu relatiile de mai jos, ne conduc la expresia analitica a relatiei de echilibru:

Aceasta inecuatie (scrisa explicit) delimiteaza o intreaga zona pe suprafata S in care punctul material este in echilibru.

b) echilibrul punctului material situat pe o curba aspra

Consideram in cele ce urmeaza situatia elementara in care p.m. este obligat sa ramana permanent pe curba aspra C, modelata matematic prin sistemul de ecuatii implicite carteziene

sub actiunea unui sistem de forte directe de rezultanta .

Daca notam cu indicii n, respectiv t componentele normala si tangentiala la curba si cu aceleasi componente ale reactiunii, ecuatiile de echilibru vor avea aceeasi forma ca cele pentru suprafata aspra, diferenta fiind ca avem cele doua relatii de legatura corespunzatoare curbei.

Discutie:

In acest caz, nu se utilizeaza unghiul a ca mai sus (nu prea are sens sa il definim!), ci unghiul b dintre rezultanta si tangenta la curba; conditia unghiulara de nealunecare devine atunci

ceea ce presupune de asta data, din punct de vedere geometric, ca echilibru sa se realizeze daca si numai daca rezultanta fortelor directe este in afara conului de frecare care are axa situata pe tangenta la curba, iar generatoarele sale formeaza unghiul cu tangenta la curba.

Conditia unghiulara se transpune in conditia analitica

Notand cu t_x, t_y, t_z proiectiile vectorului tangent la curba in punctul P, , aceasta conditie devine:

care determina o portiune a curbei in care punctul material este in echilibru.