Statica solidului rigid

Statica solidului rigid

In cazul solidului rigid avem de-a face, in cazul general cu sisteme de forte active si de legatura ce se reduc la cate un torsor complet; ca urmare, starea de echilibru va fi descrisa sistemul general de ecuatii stabilit anterior:

explicitata conform consideratiilor anterioare (numai relatiile intre forte) astfel:

intr-un reper cartezian, avem:

relatii vectoriale:

relatii intre componentele carteziene:

In continuare vom considera, ca si pentru sistemele mecanice anterioare, situatiile elementare cu privire la tipul de forte ce actioneaza asupra solidului rigid.

1. Echilibrul rigidului liber

In acest caz dispar din sistemul general conditiile de legatura si inegalitatile de frecare. Raman, practic doar sistemele de relatii anterioare scrise in diverse forme.

Acest caz permite insa o modelare matemati 212j95c ca simpla, matriciala, prin trecerea la coordonate pluckeriene, conform urmatoarelor consideratii:

Fie o dreapta (D) de versor . Conform unor discutii anterioare, momentul fortei din sistemul de forte directe ce actioneaza asupra rigidului fata de dreapta D se poate exprima prin relatia

unde este momentul versorului dreptei fata de polul O, , iar este momentul fortei fata de acelasi pol, . Daca sumam aceste relatii dupa i, obtinem relatia globala:

fiind momentul global al sistemului de forte fata de dreapta (D): , iar celelalte fiind componentele torsorului de reducere al sistemului de forte in raport cu punctul O.

In notatiile pluckeriene descrise anterior, avem:

Si astfel momentul sistemului de forte fata de dreapta (D) se poate scrie ca produsul scalar al celor doi vectori in spatiul 6 – dimensional pluckerian:

Sa consideram acum 6 drepte independente (D₁),…, (D₆); coordonatele pluckeriene ale acestora determina o matrice 6 x 6 cu determinantul nenul, . Sa consideram ca momentele sistemului de forte in raport cu toate cele 6 drepte sunt nule, adica

Aceasta relatie matriciala reprezinta un sistem de 6 ecuatii liniare si omogene in componentele torsorului. Cum determinantul coeficientilor este nenul, acest sistem va admite doar solutia nula, adica torsorul este echivalent cu zero. Reciproca este imediata, astfel ca rezulta urmatoarea concluzie importanta:

- rigidul liber este in echilibru daca si numai daca exista sase drepte independente in raport cu care se pot scrie cele 6 relatii in coordonate pluckeriene.

2. Echilibrul rigidului supus la legaturi ideale (fara frecare)

Vom considera in continuare legaturile elementare la care poate fi supus rigidul:

1. Reazemul simplu (cupla cinematica de clasa CI)

Notiunea de rezemare se foloseste pentru a desemna simplul contact mecanic direct intre corpuri. Acest contact se poate realiza pe suprafete mai mari sau mai mici. La limita, in cazul ideal in care aceasta suprafata se reduce la un punct, spunem ca avem un contact (reazem) simplu.

Asadar: un rigid este rezemat simplu daca este obligat sa aiba permanent un punct comun cu o suprafata S sau o curba C. Reprezentarea grafica este cea din figura 30.

Fig. 30

Aceasta legatura suprima numai miscarea de translatie a rigidului pe directia normala la suprafata de contact prin punctul de contact. Ca urmare, rigidul cu reazem simplu va avea 5 grade de libertate. Dupa cum legatura suprima aceasta miscare intr-un singur sens sau in ambele, spunem ca avem o legatura unilaterala, respectiv bilaterala.

Intr-un paragraf anterior am vazut ca in cazul contactului direct a doua corpuri, se dezvolta un sistem de forte ce se reduc la un torsor, deci la o rezultanta si un moment, in raport cu un punct oarecare. In cazul reazemului simplu, toate fortele fiind concurente in punctul de contact, rezulta ca torsorul acestora este echivalent cu o forta, anume cu rezultanta sistemului, avand ca punct de aplicatie punctul de contact. Mai mult, daca reazemul considerat este si ideal, adica nu apar forte de frecare, rezulta ca componenta tangentiala a rezultantei, responsabila de frecare (), este nula. Ramane  astfel in acest caz doar componenta normala a sistemului fortelor, notata cu si numita reactiune normala.

Cu aceste consideratii, ecuatiile de echilibru generale de mai sus se reduc la forma:

sau, echivalent pe componente carteziene, cu alegerea axei Oz pe directia normalei la S in punctul de contact:

Discutii:

Din primele doua relatii rezulta, in primul rand ca rezultanta fortelor directe aplicate trebuie, la echilibru, sa fie normala pe S in punctul de contact.

Sistemul ecuatiilor de echilibru este un sistem unic determinat de 6 ecuatii cu 6 necunoscute: o componenta a reactiunii normale si cei 5 parametri de pozitie necunoscuti ai rigidului; avem deci o problema static determinata.

b) Reazemul multiplu plan

Consideram in continuare ca rigidul este obligat sa aiba mai multe puncte de reazem simplu, A₁, , A_n, necoliniare, in planul xOy. Cu aceleati consideratii ca la reazemul simplu rezulta ca sistemul fortelor de legatura se reduce la cate o forta normala pe planul xOy ce actioneaza asupra rigidului in fiecare punct de contact cu acest plan, . Sistemul ecuatiilor de achilibru devine atunci similar:

Discutii:

Din primele doua relatii rezulta ca rezultanta fortelor directe trebuie sa fie normala pe planul de sprijin, iar din ultima ca componenta momentului rezultant al acestor forte pe Oz este, de asemenea nula la echilibru.

Celelalte trei relatii permit determinarea distributiei fortelor de legatura in punctele de sprijin; aceste trei ecuatii permit insa determinarea a cel mult trei necunoscute. Cum reactiunea fiecarui punct de sprijin introduce in problema o singura necunoscuta (modulul reactiunii din punctul respectiv), rezulta ca problema poate fi static determinata numai daca numarul punctelor de sprijin este cel mult 3: .

Pentru cazul a trei puncte de sprijin vom avea determinare statica daca si numai daca determinantul coeficientilor necunoscutelor N_x, N_y, N_z din cele trei ecuatii distincte este nenul,

adica daca cele trei puncte de reazem nu sunt coliniare.

Daca punctele de reazem sunt coliniare, alegand Oy pe dreapta definita de acestea, ecuatiile de echilibru se reduc la doua:

Pentru ca problema sa fie static determinata trebuie ca fortele exterioare sa fie coplanare – pentru cazul analizat, situate in planul yOz – si solidul rigid sa se sprijine in cel mult doua puncte distincte. Reactiunile se determina in acest caz din ecuatiile de mai sus ce devin:

In practica, cu aceste ecuatii se determina, de exemplu, reactiunile unei grinzi simplu rezemata in doua puncte.

c) Articulatia simpla sferica (cupla cinematica de clasa CIII)

Articulatia simpla sferica este legatura prin care se asigura fixarea unui punct al rigidului. Se suprima astfel toate posibilitatile de translatie ale rigidului, ramanand posibile doar cele 3 de rotatie, in jurul a trei axe rectangulare ce trec prin centrul cuplei (vom avea deci trei grade de libertate).

Reprezentarea geometrica a acesteia este prezentata in figura 31.

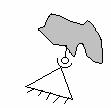
Fig. 31

Considerand aceasta legatura ca fiind rezultatul contactului mecanic punctual cu un corp fix (in reperul considerat), consideratii similare celor din cazul reazemului simplu conduc la concluzia ca sistemul fortelor de legatura ce se dezvolta trebuie sa fie la echilibru echivalent cu o reactiune unica trecand prin punctul respectiv. Ca urmare, sistemul ecuatiilor de echilibru devin:

Discutii:

Din ultimele trei ecuatii rezulta ca echilibrul rigidului supus unei astfel de legaturi este in echilibru numai daca sistemul fortelor exterioare se reduce in raport cu punctul de articulatie la o rezultanta unica al carei suport trece prin acest punct. Aceste ecuatii permit determinarea celor trei parametri de pozitie.

Primele trei ecuatii servesc la determinarea componentelor reactiunii. Se observa ca in acest caz ideal, in care legatura se realizeaza intr-un singur punct, sistemul este static determinat; nu acelasi lucru se intampla in cazul legaturii reale, cand legatura se realizeaza pe o anumita suprafata,

d) Articulatia cilindrica (cupla cinematica de clasa CIV)

Articulatia cilindrica este acea legatura a rigidului solid prin care se fixeaza o axa a acestuia – solidul se poate doar roti in jurul axei sau translata de-a lungul ei – va avea deci doar doua grade de libertate.

Alegand axa de legatura de-a lungul axei O si reducand fortele directe si pe cele de legatura in raport cu originea (un punct de pe aceastaa axa), rezulta urmatoarele: pentru a interzice numai translatiile pe Ox si Oz si rotatiile in jurul acestor axe, rezultanta fortelor si momentul rezultant al acestora trebuie sa aiba componente doar pe aceste axe. Ca urmare, sistemul ecuatiilor de echilibru devine in acest caz:

Discutii:

Conform celei de-a doua si a patra ecuatii, echilibrul solidului rigid supus acestei legaturi este posibil numai daca torsorul fortelor directe date se reduce fata de un punct de pe axa de rotatie la un torsor ale carui elemente sunt continute intr-un acelasi plan perpendicular pe aza de rotatie.

Celelalte 4 ecuatii permit deteminarea unica a celor doua componente ale reactiunii si celor doi parametri ai pozitiei de echilibru corespunzatori celor doua grade de echilibru.

e) Articulatia de rotatie (cupla rotoida de clasa CV)

Aceasta legatura este una de tip articulatie cilindrica, dar in plus se interzice si miscarea de translatie a solidului pe axa de rotatie. Solidul are deci o singura posibilitate de rotatie – deci un singur grad de libertate.

In ceea ce priveste fortele de legatura, in plus fata de situatia anterioara, mai avem si componenta pe Oy a rezultantei de legatura; astfel, ecuatiile de echilibru devin:

Discutii:

Din cea de-a patra ecuatie rezulta ca este posibil echilibrul rigidului supus la acest tip de legatura numai daca momentul rezultant al sistemului de forte directe este situat intr-un plan perprndicular pe axa de rotati ( componenta sa pe axa de rotatie este nula).

Celelalte 5 ecuatii permit deteminarea unica a celor 5 componente ale reactiunii si parametrului de pozitie de echilibru corespunzator unicului grad de echilibru.

f) Incastrarea

Incastrarea este legatura ce suprima corpului toate cele 6 grade de libertate.

In acest caz vom avea un torsor complet al fortelor de legatura. Ecuatiile de chilibru vor fi atunci cele generale:

Discutii:

Aceste relatii arata ca solidul rigid va fi in echilibru in acest caz numai daca torsorul fortelor directe este egal si opus celui al fortelor de legatura.

Cele 6 ecuatii permit determinarea unica a necunoscutelor (stare static determinata): cele 6 componente ale torsorului de reducere al fortelor de legatura.

g) Legatura prin fire sau bare articulate

Legatura prin fir sau bara articulata este echivalenta cu rezemarea simpla, ea suprimand rigidului un singur grad de libertate. Spre deosebire de acesta, in acest caz se cunoaste directia reactiunii normale: axa firului intins sau a barii. Mai mult, in cazul firelor, conditia ca acestea sa fie intinse ne da si sensul reactiunii: de la rigid catre punctul de ancorare al firului.

3. Echilibrul rigidului supus la legaturi cu frecare

Fata de situatiile precedente, modelul matematic al fortelor de legatura, torsorul acestora, va cuprinde si componentele tangentiale, in legatura directa cu frecarea. Acestor componente, la echilibru, li se vor impune conditiile corespunzatoare: de nealunecare, de nerostogolire, respectiv de nepivotare.