Am
mentionat ca integrarea ecuatiilor Hamilton (sau Lagrange)
pentru un sistem cu ![]() grade de libertate
duce la aparitia a
grade de libertate
duce la aparitia a ![]() constante arbitrare,
astfel ca solutiile ecuatiilor Hamilton se vor prezenta sub
forma:
constante arbitrare,
astfel ca solutiile ecuatiilor Hamilton se vor prezenta sub
forma:
|
|
|
(II.55) |
Pentru
sistemele izolate sau situate īn cāmpuri de forte constante īn timp, toate
momentele sunt echivalente, deci se poate lua drept una din constante momentul
initial ![]() , care poate fi ales arbitrar. Rezulta: 252c25c
, care poate fi ales arbitrar. Rezulta: 252c25c
|
|
|
(II.56) |
Eliminānd
timpul din aceste relatii, se pot exprima cele ![]() constante arbitrare
ramase ca functii de variabilele canonice, independente de timp:
constante arbitrare
ramase ca functii de variabilele canonice, independente de timp:
|
|
|
(II.57) |
Aceste functii de variabilele canonice care īsi pastreaza valoarea constanta īn timpul miscarii se numesc integrale prime ale miscarii si satisfac conditiile:
|
|
(II.58) |
Din relatia (II.51) se deduce:
|
|
|
(II.59) |
deci paranteza Poisson a
functiei Hamilton cu o integrala prima a miscarii este
nula. Reciproca este si ea valabila: orice functie de
variabilele canonice care nu depinde explicit de timp si a carei
paranteza Poisson cu functia Hamilton ![]() este nula, este o
integrala prima a miscarii.
este nula, este o
integrala prima a miscarii.
Īn legatura cu integralele prime ale miscarii se poate enunta si demonstra [1], [2], [7] teorema lui Poisson:
Daca
doua functii ![]() si
si ![]() sunt integrale prime
ale miscarii, atunci si paranteza lor Poisson este tot
integrala prima a miscarii.
sunt integrale prime
ale miscarii, atunci si paranteza lor Poisson este tot
integrala prima a miscarii.
Cunoscānd integralele prime ale miscarii - adica marimile fizice care ramān constante īn cursul evolutiei sistemului - putem caracteriza comportarea sistemelor īn urma interactiilor.
Aceasta
lege decurge din uniformitatea curgerii timpului. Din aceasta proprietate
rezulta ca ecuatiile de miscare pentru un sistem īnchis sau
īn cāmpuri de forte constante īn timp sunt invariante la o translatie
īn timp, deci functia Lagrange si functia Hamilton nu depind
explicit de timp, adica ![]()
Cum din (II.51) rezulta ca:
|
|
(II.60) |
iar ![]() (proprietatea 3 a
parantezelor Poisson), rezulta:
(proprietatea 3 a
parantezelor Poisson), rezulta:
|
|
(II.61) |
Aceasta
lege poate fi demonstrata si cautānd ![]() , tinānd cont ca
, tinānd cont ca ![]() nu contine
explicit timpul:
nu contine
explicit timpul:
|
|
(II.62) |
Din ecuatiile Lagrange:
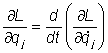
iar (II.62) devine:
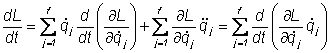
sau
|
|
(II.63) |
de unde
|
|
(II.64) |
Fiindca
energia potentiala ![]() nu depinde de vitezele
generalizate
nu depinde de vitezele
generalizate
|
|
(II.65) |
si folosind relatia (II.47) obtinem:
|
|
(II.66) |
Atunci relatia (II.64) devine:
![]()
sau
|
|
(II.67) |
Aceasta
lege decurge din proprietatea de omogeneitate a spatiului. Din
aceasta proprietate rezulta ca starea mecanica a unui
sistem īnchis nu se schimba īn urma unei translatii infinitesimale cu
![]() a tuturor punctelor
sistemului. O astfel de translatie va lasa nemodificata
hamiltoniana sistemului, deci variatia functiei
a tuturor punctelor
sistemului. O astfel de translatie va lasa nemodificata
hamiltoniana sistemului, deci variatia functiei ![]() la translatia cu
la translatia cu ![]() este nula:
este nula:
![]()
![]() , de unde
, de unde
|
|
(II.68) |
Consideram
proprietatea 6) b) a parantezelor Poisson īn care ![]()
|
|
|
(II.69) |
Sumānd īn ambii membri ai egalitatii (II.69) pentru toate particulele sistemului:
|
|
(II.70) |
Dar ![]() - impulsul total al
sistemului si din (II.70) rezulta:
- impulsul total al
sistemului si din (II.70) rezulta:
|
|
(II.71) |
Cum pentru
sisteme izolate ![]() nu depinde explicit de
timp, rezulta ca:
nu depinde explicit de
timp, rezulta ca:
|
|
(II.72) |
Conservarea momentului cinetic al unui sistem rezulta din proprietatea de izotropie a spatiului: proprietatile mecanice ale unui sistem īnchis nu se schimba īn cursul unei rotatii de ansamblu, īn spatiu, a sistemului.
Sa consideram un punct material care efectueaza o miscare de rotatie īn jurul axei Oz (fig.II.3)
Fie ![]() unghiul de
rotatie corespunzator deplasarii elementare
unghiul de
rotatie corespunzator deplasarii elementare ![]() .
.
Se defineste vectorul de rotatie
infinitesimala ![]() ca vectorul perpendicular
pe planul traiectoriei, avānd sensul dat de regula burghiului si modulul
ca vectorul perpendicular
pe planul traiectoriei, avānd sensul dat de regula burghiului si modulul ![]() .
.
|
Fig.II.3 |
Din figura
II.3 se observa ca ![]() si date fiind
orientarile vectorilor
si date fiind
orientarile vectorilor ![]() si
si ![]() se poate scrie:
se poate scrie:
|
|
(II.73) |
Rotatia
modifica si vectorul viteza al particulei cu cantitatea ![]() care satisface
relatia
care satisface
relatia
|
|
(II.74) |
deci si impulsul va varia cu
|
|
(II.75) |
Consideram
un sistem de ![]() puncte materiale care
efectueaza o rotatie cu acelasi unghi
puncte materiale care
efectueaza o rotatie cu acelasi unghi ![]() . Din invarianta la o asemenea rotatie a
proprietatilor mecanice ale sistemului rezulta invarianta
functiei Hamilton (si a functiei Lagrange), deci:
. Din invarianta la o asemenea rotatie a
proprietatilor mecanice ale sistemului rezulta invarianta
functiei Hamilton (si a functiei Lagrange), deci:
|
|
(II.76) |
|
|
(II.77) |
Folosind proprietatea produsului mixt
![]()
obtinem:
|
|
(II.78) |
Din proprietatile 6) a) si 6) b) ale parantezelor Poisson avem:
![]()
iar (II.78) devine:
|
|
(II.79) |
Proprietatea
5) a parantezelor Poisson scrisa pentru trei functii vectoriale ![]() face ca expresia
(II.79) sa devina:
face ca expresia
(II.79) sa devina:
|
|
(II.80) |
sau
|
|
(II.81) |
Īn
expresie apare momentul cinetic al punctului material ![]() si momentul
cinetic total al sistemului
si momentul
cinetic total al sistemului ![]() , deci (II.81) se poate scrie:
, deci (II.81) se poate scrie:
|
|
(II.82) |
si cum pentru un
sistem īnchis momentul cinetic ![]() nu depinde explicit de
timp
nu depinde explicit de
timp 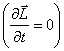 , rezulta:
, rezulta:
|
|
(II.83) |
deci momentul cinetic total se conserva.
|