Transformarea modulului si directiei vitezei in TRR
Consideram doua sisteme inertiale 
si 
, si un
obiect care se deplaseaza fata de sistemul cu viteza 
(fig.10 a), iar fata de sistemul cu viteza 
(fig.10 b).
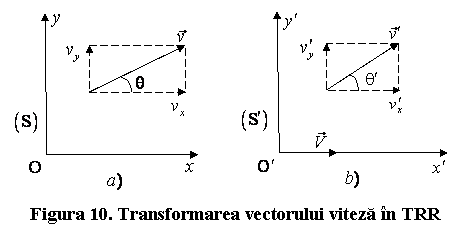
Conform legii de compunere a vitezelor (4.50) si (4.51), putem scrie:
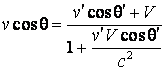(4.54)
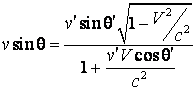(4.55)
unde s-au
folosit proiectiile vectorului pe axele 
si 
, si
proiectiile lui pe axele
si 
:
,
respectiv 
Impartind (4.55) la (4.54) obtinem:
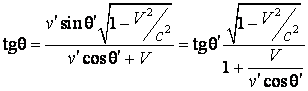(4.56)
Ridicam la patrat (4.54) si (4.55), apoi le adunam:
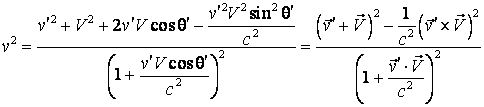(4.57)
Formulele (4.56) si (4.57) reprezinta transformarea directiei, respectiv a modulului vitezei in TRR.
Exemplul 4
Sa se deduca relatia dintre marimile 
, 
si 
, unde 
, 
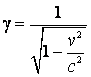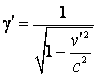si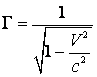 
.
Rezolvare
Se pleaca de la (4.57) si se
calculeaza expresia 
:
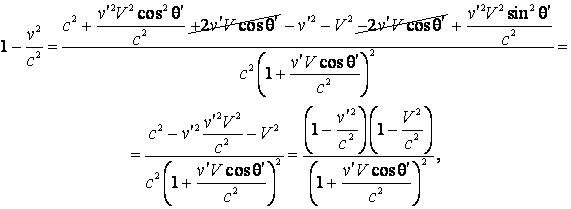
de unde rezulta:
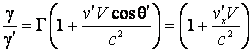(4.58)
Exemplul 5
Un sistem de referinta se deplaseaza fata de sistemul de referinta
inertial cu viteza 
, astfel ca
si 
(fig.11). O
bara situata in planul 
are lungimea proprie 
fata de si formeaza unghiul 
cu axa 
. Cunoscand
viteza luminii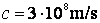 
, se cer:
a) Lungimea barei in raport cu ;
b) Unghiul format de bara cu axa 
, masurat
fata de ;
c) Viteza, in raport cu , a unei
perturbatii care se propaga in lungul barei, cu viteza 
in raport cu .
Rezolvare
a)
Inlocuind in 
din (4.38), obtinem:
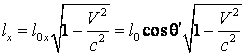
si tinand cont ca 
, obtinem:
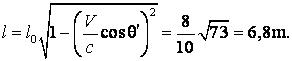
b)
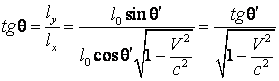
c)
Scriem legea compunerii vitezelor pe coordonatele si 
(4.47) si (4.48):
si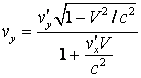 
,
Tinand cont ca
, 
,
si inlocuind (4.47) si (4.48) in
obtinem:
|
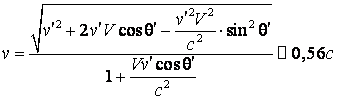
