Transformarile Lorentz speciale
Pe
baza principiilor noi aduse de TRR se obtin relatiile de transformare Lorentz
speciale, valabile in cazul simplificat al unui sistem de referinta 
care se deplaseaza in lungul axe 838d37i i 
(fig.8). In aceste conditii noile transformari
trebuie sa treaca, in cazul 
, in
transformarile Galilei (4.18) si (4.19) .
Presupunem
ca intre coordonatele 
si 
exista o relatie de forma:
(4.25)
unde 
este un coeficient de proportionalitate care
nu depinde nici de si nici de 
, dar poate
fi functie de 
. Deoarece
ecuatiile ce exprima legile fizicii au aceeasi forma in sistemele de referinta 
si , putem
inversa sensul vitezei si sa scriem corespunzator dependenta lui de si 
:
(4.26)
Coeficientul de proportionalitate trebuie sa fie identic pentru ambele sisteme
de referinta, deoarece intre si nu exista nici o deosebire, in afara de sensul
vitezei 
. Daca
introducem pe din (4.25) in (4.26), obtinem:
de unde
(4.27)
Din (4.27)
rezulta deci ca intervalele de timp si sunt identice numai in cazul fizicii clasice,
cind 
.
Sa
utilizam al doilea postulat al teoriei relativitatii restrinse. Admitem ca la
momentul 
originile 
si 
ale celor doua sisteme de referinta coincid.
Din aceste doua origini comune ale sistemelor de referinta se emite la
momentul 
un semnal luminos, care poate fi observat atit
in cat si in . Conform
principiului b), observatorii aflati in repaus in raport cu si respectiv in raport cu trebuie sa constate aceeasi viteza 
de propagare a semnalului. Asadar, pentru
observatorul din ecuatia frontului undei este:
(4.28)
iar pentru observatorul din ecuatia frontului undei este:
(4.29)
Introducem in (4.29) pe din (4.25) si pe din (4.27):
(4.30)
de unde obtinem:
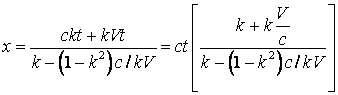
sau
(4.31)
Relatia (4.31) coincide cu (4.28) daca termenul din paranteza dreapta este egal cu unu, adica:
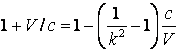
de unde obtinem expresia factorului :
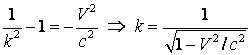(4.32)
Ca
si la transformarile lui Galilei (4.18) si (4.19), nu exista indicatii ca ar
exista deosebiri intre perechile de coordonate 
si respectiv 
, orientate
perpendicular pe viteza , astfel ca
putem scrie:
(4.33)
Din formulele (4.25), (4.26), (4.27), (4.32) si (4.33) obtinem relatiile de transformare Lorentz speciale:
(4.34)
si respectiv:
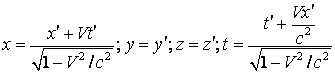(4.35)
Se observa simplu ca pentru 
transformarile Lorentz (4.34) si (4.35) trec
in transformarile Galilei (4.18) si (4.19).
|
