ARBORI BINARI DE CAUTARE

ARBORI BINARI DE CĂUTARE .

Īn acest capitol vom īnvata:

Ce sunt arborii binari de cautare

Ce operatii se fac cu acsti arbori

Care este complexitatea acestor algoritmi

Arborii de cautare sunt structuri de date care suporta foarte multe operatii cum ar fi : SEARCH (cautare), MINIMUM, MAXIMUM, PREDECESOR, SUCCESOR, INSERT (introducere) si DELETE (stergere). Un arbore de cautare poate fi folosit atāt ca dictionar cāt si ca o coada de prioritati.

Operattiile de baza pe un arbore binar de cautare au timpul proportional cu

īnaltimea arborelui. Pentru un arbore binar complet aceste operatii se executa īn cel mai rau caz īn O(lg n). Daca arborele este o īnlantuire liniara de n noduri atunci aceleasi operatii se vor face īn cel mai rau caz īn O(n).

Īn practica nu putem garanta īntotdeauna randomizarea co 727b11h nstruirii arborilor de cautare, dar sunt anumiti arbori binari de cautare (arborii rosu-negru, arborii balansati) ale caror performante sunt bune pentru operatiile de baza, chiar si īn cel mai rau caz.

8.1.Ce este un arbore binar de cautare?

Un arbore binar de cautare este organizat, dupa cum ne sugeraza si numele, ca un arbore binar cum vedem īn figura 8.1

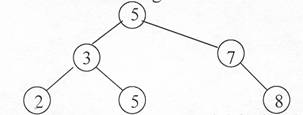
fig.8.1

Acesta este un arbore binar de cautare cu 6 noduri si īnaltime 2.

Un asemenea arbore poate fi reprezentat de o structura de date īnlantuita īn care fiecare nod este un obiect. Īntr-un nod x avem |KEY | ADR | LS | LD | P | KEY(x) īnsemna valoarea cheii din nodul x, informatia de lānga KEY se mai numeste si informatie satelit (SAT), legatura la copilul din stānga, legatura la copilul din dreapta, si parintele nodului x. Daca un copil sau un parinte lipsesc, cāmpul corespunzator va contine NIL. Fie un arbore care contine aceleasi chei cu cel din fig.8.l dar cu īnaltimea 4 si mai putin eficient a carui reprezentare o gasiti īn figura 8.2.

Definitie Un arbore binar de cautare este un arbore binar care satisface conditia:

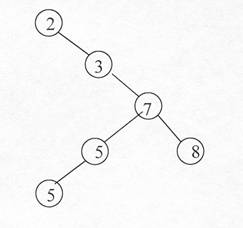
fig.8.2.

a) Pentru orice nod y care se afla īntr-un subarbore stāng al nodului x

KEY(y) ~ KEY(x)

b) Pentru orice nod y care se afla īntr-un subarbore drept al nodului x

KEY(x) ~ KEY(y)

Aceasta proprietate a unui arbore binar de cautare ne permite sa extragem toate cheile sortate cu ajutorul unui simplu algoritm recursiv printr-o parcurgere īn inordine.

INORD_PARC (x)

Daca LS(x) NIL atunci

Cheama INORD_P ARC(LS(x))

Scrie KEY (x)

Cheama INORD_P ARC(LD(x))

Sdaca

8.2.Operatii asupra unui arbore binar de cautare.

Cea mai comuna operatie efectuata asupra unui arbore binar de cautare este cautarea unei chei memorata īn arbore careia īi vom spune cautare binara.

Aceasta structura mai suporta si interogari de tipul "care este Minimum-ul, Maximum-ul, Succesor-ul, Predecesor-ul?".

Īn continuare vom examina aceste operatii si vom vedea ca fiecare se poate face īntr-un timp proportional cu īnaltimea arborelui, deci O(h).

Īn figura 8.3 vom exemplifica care este calea de cautare a cheii 13.

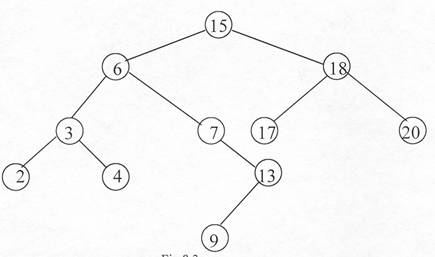
Fig.8.3.

Cautarea cheii 13 trebuie facuta pe partea stānga a radacinii - 15, unde gasim cheia 6, deci cautarea trebuie continuata pe partea dreapta, unde gasim cheia 7, vom continua cautarea pe partea dreapta si gasim cheia 13. Calea acestei cautari este: 15-6-7-13.

Vom folosi urmatorul algoritm pentru a cauta īntr-un arbore binar de cautare un nod cu cheie data:

CAUT_BIN(Rad, k, Rez)

x=Rad

Atat timp cat x Nil si k KEY(x)

Daca k <KEY(x) atunci

x = LS(x)

altfel

x = LD(x)

Sdaca

Sciclu

Daca x = Nil atunci

Rez =Nil

altfel

Rez =ADR(x)

Sdaca

return

MINIMUM si MAXIMUM.

Un element al unui arbore binar de cautare, a carui cheie este minima, poate fi gasit urmarind pointerele descendentilor din partea stānga īncepānd de la radacina pāna cānd este īntālnita o adresa = Nil.

Urmatorul algoritm determina nodul de cheie minima a unui arbore cu radacina Rad:

MIN_BIN (Rad, Min) x = Rad

Atat timp cat LS(x) Nil

x = LS(x)

Min=KEY(x)

Return

Exercitiul 1.

Algoritmul pentru determinarea nodului cu cheia maxima este simetric cu cel de mai sus si va propunem sa-l scrieti aici:

SUCCESOR si PREDECESOR

Fiind dat un nod īntr-un arbore binar de cautare, cāteodata este important sa-i gasim succesorul īn sirul sortat al cheilor obtinut prin parcurgerea īn inordine. Daca toate cheile sunt distincte succesorul unui nod x este nodul cu cea mai mica cheie, mai mare decāt KEY(x). Structura arborilor binari de cautare ne permite sa determinam succesorul unui nod fara a compara vreodata cheile.

Urmatorul algoritm determina succesorul nodului x daca acesta exista si returnaza Nil daca x este cea mai mare cheie din arbore:

SUCC_BIN(x, y)

Daca LD(X) Nil atunci

Cheama MIN_BIN(LD(x), y)

Return

sdaca

y =P(x)

Atat timp cat y Nil si KEY(y)<KEY(x)

x=y

y = P(y)

sat

Return

Algoritmul pentru succesor este rupt īn doua cazuri:

Daca sub arborele drept al nodului x nu este gol, atunci succesorul lui x este cel mai din stānga nod al subarborelui drept, pe care īl gasim chemānd MIN_BIN. Daca subarborele drept al nodului x este gol si x are un succesor y, atunci y este cel mai mic stramos al lui x si copilul stāng al lui y este deasemenea un stramos al lui x.

Exercitiul 2.

Algoritmul pentru determinarea predecesorului este simetric cu cel de mai sus si īl lasam ca exercitiu pentru cititor.

INSERAREA si sERGEREA

Operatiile de inserare si stergere aplicate unei multimi dinamice reprezentate de un arbore binar de cautare cauzeaza schimbari īn arbore. Structura de date trebuie modificata ca sa reflecte aceste schimbari, dar proprietatile arborelui binar de cautare trebuie sa fie īn continuare pastrate. Modificarea arborelui pentru inserarea unui unui element este relativ directa, īn schimb la stergere este ceva mai complicat.

INSERAREA

Pentru inserarea unei noi valori īntr-un arbore binar de cautare T vom folosi algoritmul INS_BIN. Aceasta procedura este exemplificata īn figura 9.4:

Īn aceasta figura nodurile umbrite marcheaza calea de la radacina pāna la pozitia īn care se face inserarea. Linia punctata indica legatura īn arbore care este adaugata pentru inserarea elementului. (cheia elementului care se insereaza este 13).

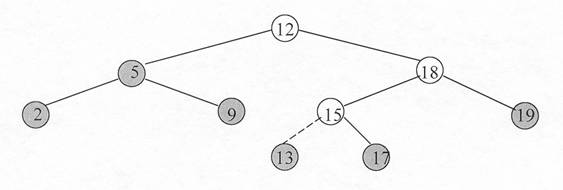
fig.5. 4

INS_BIN(x ,y)

y = Nil

x = Rad

LS(z) = LD(z)=Nil

Atata timp cat x Nil

y=x

Daca KEY(z)<KEY(x) atunci

x = LS(x)

altfel

x = LD(x)

sdaca

Sciclu

P(z)=y

Daca y = Nil atunci

Rad = z

altfel

Daca KE Y ( z) < KE Y (y) atunci

LS(y) = z

altfel

LD(y) = z

Sdaca

Sdaca

Return

sTERGEREA.

Algoritmul pentru stergerea unui nod dat - z dintr-un arbore binar de cautare are ca argument un pointer catre z. Procedura considera trei cazuri ilustrate īn figura 8.5:

Daca z nu are copil modificam parintele lui z īnlocuindu-l pe z cu Nil.

Daca z are un singur copil īl eliminam pe z facānd o noua legatura īntre copilul si parintele lui z.

Daca z are doi copii īl eliminam pe z prin īnlocuirea continutului sau cu cel al succesorului sau care nu are copil stāng.

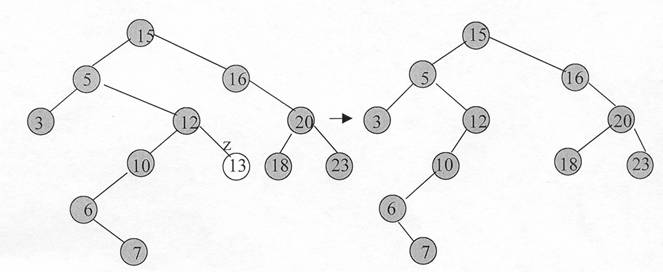
Fig. 8.5 a ) cānd z nu are copil:

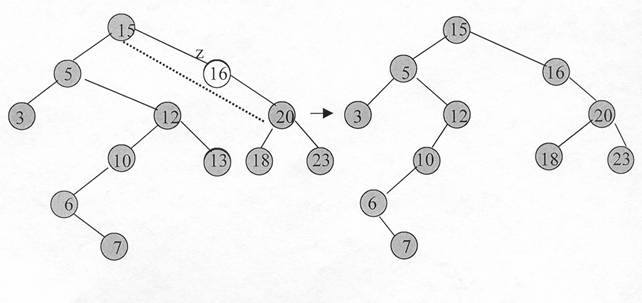
b ) cānd z are un singur copil:

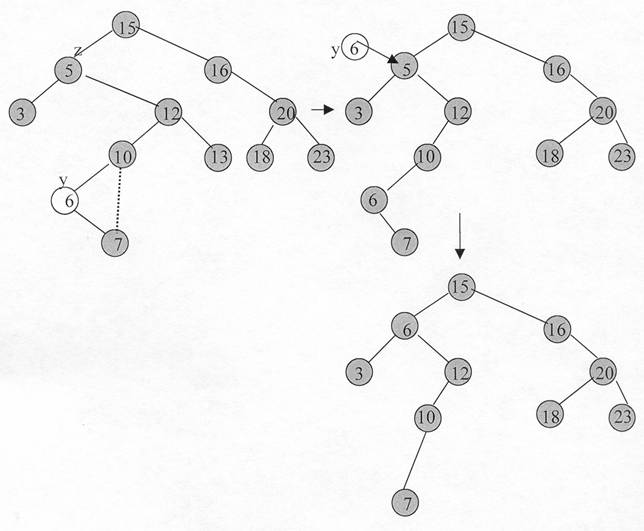
c ) cānd z are doi copii

ELIMIN_BIN (T ,z)

Daca LS(z)=Nil sau LD(z)=Nil atunci

y=z

altfel

cheama SUCC_BIN(z ,y)

sdaca

Daca LS(y) Nil atunci

x =LS(y)

altfel

x=LD(y)

sdaca

Daca x Nil atunci

P(x) = P(y)

sdaca

Daca P(y) = Nil atunci

Rad = x

altfel

Daca y=LS(P(y)) atunci

LS(P(y)) = x

altfel

LD(P(y)) = x

Sdaca

sdaca

Daca KE Y ( z) < KE Y (y) atunci

KEY(z) = KEY(y)

ADR(z) = ADR(y)

Sdaca

Return

Īntrebari si exercitii la capitolul 8.

Exercitiile 1 si 2 se gasesc īn text.

Exercitiul 3.

Scrieti algoritmul de  cautare binara recursiv.