ARBORI BINARI.
În acest capitol vom învata:
Ce sunt arborii binari
Cum se memoreaza ei
Cum se parcurg arborii binari
Cum se transforma un arbore oarecare 818c28i în arbore binar
Ce este un nomenclator
Un arbore în care orice vârf are zero, unul sau doi descendenti se numeste arbore binar. Un arbore binar care are numai vârfuri cu nici un descendent sau cu doi
descendenti se numeste arbore strict binar. (Un astfel de arbore de foloseste, de
exemplu, la reprezentarea în memorie
a unei expresii aritmetice.)
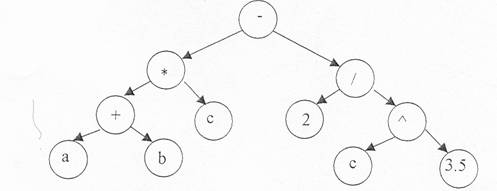
Exemplu: expresia (a+b)*c - 2/c^3.5 unde (x^y înseamna ' x la puterea y') - se va reprezenta astfel :
fig. 6.1
Frunzele acestui arbore ( nodurile fara descendenti) contin operanzii, iar celelalte noduri contin operatiile. Deoarece nu toate operatiile sunt comutative este foarte important daca un nod este descendent pe stânga sau pe dreapta. Radacina unui arbore este nodul care nu este descendentul nici unui nod.
Alocarea unui arbore binar se poate face: secvential, înlantuit sau mixt.
Alocarea secventiala a unui arbore binar
În vectorul (x(I))I=l,n) vom avea urmatoarele reguli:
radacina este în x(1)
pentru fiecare nod x(I) descendentul din stânga este x(2*I) iar cel din dreapta este x(2 *I+1)
daca nu exista descendent se pune '*'.

Reprezentarea secventiala a arborelui din fig. 1 este :
Observatie : x(20), ... , x(27) sunt pozitii din vector neutilizate.Vom folosi aceasta alocare în capitolul destinat cozilor de prioritate pentru a construi o structura asemanatoare denumita HEAP.
Exemple de parcurgeri:
1- parcurgerea arborelui din fig.6.1 în preordine -,*,+,a,b,c,2,/,^,c,3.5
aceasta scriere se nmeste scriere poloneza prefixata pentru o expresie aritmetica.
2- parcurgerea arborelui din fig. 1 în inordine a,+,b,*,c,-,2,/,c,^,3.5
aceasta este scrierea obisnuita a expresiilor matematice (operatiile sunt scrise în ordinea efectuarii lor).
3- parcurgerea arborelui din fig. 1 în postordine a,b,+,c, *,2,c, ^,3.5,/,-
aceasta scriere se numeste scriere poloneza postfixata a unei expresii aritmetice.
PREORD_IT(RAD)
STIVA = F
P=RAD
Daca P ' * ' atunci
Scrie INFO(P); P=>STIVA
P=LS(P) Cicleaza
altfel
EXIT
Sdaca
sciclu
Daca STIVA = F atunci EXIT
Altfel
P<=STIVA ; P= LD(P)
Sdaca
Sciclu
Return
Algoritmul se poate modifica usor pentru INORDINE_IT, dar pentru POSTORDINE_IT este nevoie de doua stive.
Exercitiul 1.
Scrieti algoritmul pentru inordine iterativ.
Exercitiul 2.
Scrieti algoritmul pentru postordine iterativ.
Un exemplu des folosit este structura unui produs format din ansamble, subansamble si asa mai departe pâna la piese simple. Aceasta structura da nastere unui arbore oarecare cum ar fi cel din figura 6.2.
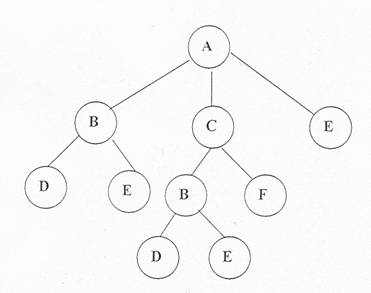
Fig.6.2
Exista o metoda de a construi un arbore asociat care, de
aceasta data, este binar. Transformarea se face în felul urmator
: pentru fiecare nod descendentul din dreapta este fratele urmator
(elementul urmator aflat la acelas nivel de descompunere). Astfel
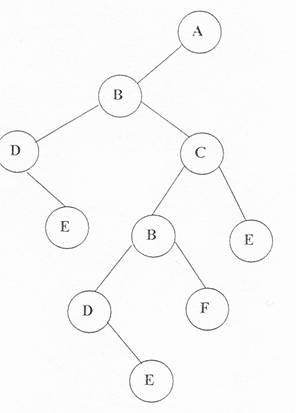
arborele din fig.6.2 da nastere unui arbore binar ca cel din fig.6.3.
Fig 6.3.

Parcurgerea în preordine a acestui arbore binar asociat da
aceeasi ordine a nodurilor ca si parcurgerea în adâncime a arborelui
oarecare initial (fapt pentru care se spune câte odata ordine de
parcurgere în preordine pentru arborele oarecare). Lista parcurgerii în
preordine în acest caz concret este nomenclatorul de produse si este o
lista reprezentativa care intra în reclama produsului. Ea arata în felul
urmator:
Diagrama E-R conceptuala pentru nomenclatorul de produse arata în prima instanta asa:
Repere = (CodRep, Denum,. . .)
Stuctura = (CodRep,CodRep,Cant)
De exemplu, pentru arborele de mai sus, se obtin instantele:

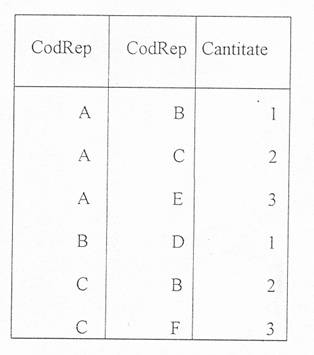
Repere Structura Structura
Întrebari si exercitii la capitolul 6.
Exercitiile 1 si 2 sunt în text referitoare la parcurgerea arborilor binari în inordine si postordine nerecursiv.
Exercitiul 3.
Se da A,B,C,D,E,F,G,H parcurgerea în preordine a unui arbore binar si
B,A,E,D,C,F,H,G parcurgerea în inordine a aceluiasi arbore. Sa se deseneze arborele.
Exercitiul 4.
Sa se scrie algoritmul pentru exercitiul 3.
|