Algoritmi probabilisti

Algoritmi probabilisti

În multe probleme, în timpul rezolvarii, putem ajunge la un moment dat în situatia de a avea de ales între mai multe variante de continuare. Am vazut ca în aceasta situatie putem analiza pe rând variantele, putem încerca sa determinam varianta optima si sa o urmam etc.

Algoritmii probabilisti adopta o alta abordare: se alege aleator una dintre variante. Vom vedea ca în unele situatii aceasta abordare poate conduce la determinarea mai rapida a unei solutii (exacte sau aproximative).

Pentru alegerea aleatoare se presupune ca avem la dispozitie o functie random, care întoarce o valoare aleatoare dintr-un interval [a,b) de numere reale sau dintr-o secventa a..b de numere întregi consecutive.

Este evident ca la executari diferite ale unui algoritm probabilist, rezultatele sunt în general diferite.

Exista trei categorii mari de algoritmi probabilisti, pe care le prezentam în continuare.

Algoritmi numerici

Algoritmii de acest tip sunt caracterizati prin urmatoarele:

urmaresc determinarea aproximativa a unei valori;

cu cât timpul alocat executarii algoritmului este mai mare, precizia rezultatului se îmbunatateste.

Exemplul 1. Acul lui Buffon.

Se considera o multime de linii paralele astfel încât oricare doua linii vecine sunt la distanta de o unitate. Un ac (segment) de lungime o jumatate de unitate este aruncat aleator si se numara de câte ori a intersectat vreo linie.

Se poate demonstra ca probabilitatea ca acul sa intersecteze o linie este 1/p. Practic, dupa un numar "suficient de mare" de încercari, raportul între:

numarul total de încercari si

numarul cazurilor în care acul a intersec 828b12i tat vreo linie

va fi "suficient de aproape" de p

Exemplul 2. Se arunca repetat cu o sageata într-un panou patrat. Se presupune ca sageata nimereste totdeauna panoul. Atunci raportul dintre:

numarul cazurilor în care sageata nimereste în cercul înscris în patrat si

numarul total de încercari

tinde la p/4, numar egal cu raportul dintre aria cercului înscris în patrat si aria patratului.

Exemplul 3. Data fiind o functie f:[a,b] [c,d], se cere determinarea aproximativa a valorii I=.

Un algoritm probabilist de tip numeric pentru determinarea valorii I este urmatorul:

s

for i=1,n

x random([a,b]); s s+f(x)

s s^.(b-a)/n

write(s)

Algoritmi Monte Carlo

Algoritmii de acest tip urmaresc determinarea unei solutii exacte si sunt caracterizati prin urmatoarele:

furnizeaza totdeauna un rezultat, care însa nu este neaparat corect;

probabilitatea ca rezultatul sa fie corect creste pe masura ce timpul disponibil creste.

Exemplul 4. Se considera vectorul x=(x₁,...,x_n) cu elemente distincte. Se cere determinarea unui element al vectorului care sa fie mai mare sau egal cu media aritmetica a celor n numere.

Problema are sens daca valoarea lui n este foarte mare, iar timpul avut la dispozitie este mic (în caz contrar alegem, în timp liniar, cel mai mare element al vectorului, care satisface evident conditia data).

Un algoritm probabilist de tipul Monte Carlo este urmatorul: alegem aleator un element al vectorului si repetam aceasta operatie fara a depasi timpul disponibil, pastrând într-o variabila v cel mai mare dintre elementele alese. Rezultatul este v

Sa presupunem ca în timpul disponibil am analizat k elemente ale vectorului; v este cel mai mare dintre ele. Valoarea v nu îndeplineste conditia din enunt numai în cazul când toate cele k elemente alese sunt mai mici decât media aritmetica a elementelor lui x. Cum probabilitatea ca un element sa fie mai mic decât media aritmetica este 1/2, probabilitatea ca toate elementele (deci si v) sa fie mai mici ca media aritmetica este . Rezulta ca probabilitatea ca valoarea întoarsa de algoritm sa fie corecta este . De exemplu pentru k=20, aceasta probabilitate este mai mare decât 0,999999.

Exemplul 5. Fie G un graf neorientat. Vom întelege prin mutare eliminarea unui vârf împreuna cu toti vecinii sai. Se cere numarul minim de mutari prin care se pot elimina toate vârfurile.

Aceasta problema a fost propusa la o olimpiada scolara pe timpul când programul era rulat pe 10 exemple si se contabiliza numarul de exemple pentru care rezultatul furnizat este corect.

Pentru a "aduna" puncte, nu este necesar sa ne gândim la o solutie efectiva, ci este suficient sa aplicam urmatorul algoritm probabilist:

se alege aleator un vârf si se elimina împreuna cu vecinii sai;

se repeta pasul anterior pe noul graf pâna când sunt eliminate toate vârfurile;

se memoreaza numarul de mutari efectuat.

Se reia algoritmul (fara a depasi timpul maxim fixat pentru un test) si se pastreaza cel mai mic numar de mutari.

Algoritmi Las Vegas

Algoritmii de acest tip urmaresc, ca si algoritmii Monte Carlo, determinarea unei solutii exacte si sunt caracterizati prin urmatoarele:

nu furnizeaza totdeauna un rezultat, dar daca furnizeaza un rezultat atunci acesta este corect;

probabilitatea ca rezultatul sa fie corect creste pe masura ce timpul disponibil creste.

Exemplul 5. Se dau n texte (n foarte mare) cu urmatoarele proprietati:

exista un unic text t₀ care apare de cel putin 10% ori;

celelalte texte sunt distincte.

Se cere determinarea textului t₀

Problema a fost propusa la un concurs studentesc A.C.M.

Un algoritm probabilist eficient este urmatorul:

repeat

i random(1..n); j random(1..n);

if i j & t_i=t_j

then write t_i; stop

until false

Probabilitatea ca alegerea unui indice sa conduca la textul t₀ este 1/10, deci probabilitatea ca sa obtinem o pereche de indici (i,j) cu t_i=t_j=t₀ este 1/100. Cu alte cuvinte, teoretic sunt suficiente 100 de încercari, independent de valoarea lui n. Pe de alta parte este posibil ca algoritmul sa nu produca vreun rezultat într-un interval limitat de timp.

Exemplul 6. Problema celor n dame

Am prezentat o rezolvare a acestei probleme folosind metoda backtracking. Implementarea si executarea algoritmului corespunzator arata ca se ajunge la o solutie în timp "rezonabil" doar pentru valori mici ale lui n n

Un algoritm probabilist pentru aceasta problema, care furnizeaza rapid o solutie chiar pentru valori ale lui n mai mari decât 100 este urmatorul:

plasam o dama pe prima linie;

presupunând ca am plasat neantagonist câte o dama pe liniile 1,...,k-1, facem un inventar al pozitiilor posibile pentru dama de pe linia k si alegem aleator una dintre ele.

Exista doua posibilitati:

Am reusit sa plasam o dama pe linia n. Atunci am determinat o solutie, deci o listam si oprim programul;

Am ajuns la o linie k si nu exista pozitii posibile. Atunci reluam întreg algoritmul (deci nu ne întoarcem la linia precedenta ca la backtracking).

Pentru implementarea algoritmului, trebuie tinuta o evidenta a coloanelor si diagonalelor ocupate (pe care nu putem plasa o dama). Pentru aceasta vom folosi vectorii booleeni NV_SE[-n+1..n-1] NE_SV[2..2n] si C[1..n] ale caror valori ne spun daca o diagonala NV-SE, o diagonala NE-SV sau o coloana sunt libere (nu exista plasata o dama pe diagonala sau coloana respectiva).

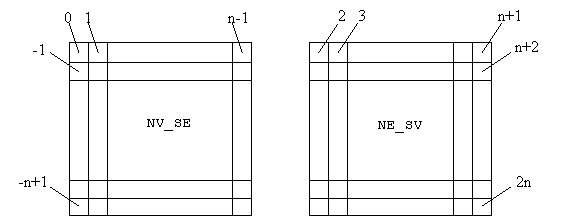
Observatie. Daca suntem pe linia k, putem plasa o dama pe coloana i daca este îndeplinita conditia:

j(k,i) C_i libera & NV_SE_i-k libera  & NE_SV_i+k libera.

În algoritmul care urmeaza, solutia este obtinuta în vectorul x=(x₁,...,x_n)

repeat

initializam componentele celor 3 vectori booleeni cu valoarea true

k

repeat

facem inventarul pozitiilor i cu j(k,i)

plasam aceste pozitii în primele na componente ale unui vector a

if na>0

then aleg aleator i ; i a_i

x_k i ; NV_SE_i-k false; NE_SV_i+k false

C_i false; k k+1

until na=0 k=n+1

until k=n+1

write(x)

Algoritmi genetici

Algoritmii genetici sunt tot algoritmi probabilisti, dar de o natura complet diferita, dupa cum vom vedea în continuare.

Algoritmii genetici reprezinta tehnici de cautare si optimizare. Denumirea lor se datoreaza preluarii unor mecanisme din biologie: mostenirea genetica si evolutia naturala pentru populatii de indivizi.

Problema generala: Fie f:D R. Se cauta max

Presupunem ca multimea D poate fi pusa în corespondenta biunivoca cu o multime C ^r, adica orice element al lui D poate fi codificat ca:

x=(x₁,...,x_r) cu x_i " i=1,...,r. Vectorul x se numeste cromozom.

Nu vom lucra cu un singur cromozom, ci cu o populatie de n cromozomi (indivizi), care se transforma prin trecerea de la o generatie la alta.

Observam deci ca spre deosebire de algoritmii iterativi uzuali de optimizare, în care la fiecare etapa se trece de la un element din C la urmatorul, în algoritmii genetici la fiecare etapa se trece de la o submultime a lui C la o alta submultime a lui C. O alta trasatura a algoritmilor genetici este ca la trecerea de la o populatie la urmatoarea, cromozomii se combina între ei.

Observatie. O populatie este un multiset (un element poate sa apara de mai multe ori).

Schimbarea de generatie se face prin selectia din populatia curenta a unei subpopulatii si modificarea acesteia prin operatiile de încrucisare (crossover) si mutatie, ce vor fi descrise mai jos. Toate populatiile succesive au acelasi numar de indivizi.

Algoritmul se încheie daca s-a efectuat un numar dat de schimbari de configuratii sau daca dupa un numar de schimbari de generatie maximul curent ramâne neschimbat. Consideram în continuare prima variantă.

Notatii:

P - populatia curenta; P=

valmax - valoarea maxima curenta ;

xmax - punctul pentru care este atinsa valmax

nmax - numarul maxim admis de schimbari de configuratii;

pc - probabilitatea de încrucisare;

pm - probabilitatea de mutatie;

r - lungimea cromozomilor;

n=|P|

Se mai foloseste o functie J:C R pentru evaluarea performantelor cromozomilor din P. În general J este corespondenta functiei f:D R

Algoritmul general este urmatorul:

P aleator; valmax

for t=1,nmax

se calculeaza valorile J(p) " p P si se actualizeaza eventual valorile xmax si valmax

etapa de selectie

etapa de încrucisare

etapa de mutatie

Scopul principal al celor trei etape este de a ne apropia cât mai mult de maxim, dar si de a acoperi prin cautari întregul domeniu de definitie, pentru a obtine maximul general si nu unul local.

Etapa de selectie urmareste pastrarea (chiar multipla) a celor mai performanti indivizi (cromozomi) ai populatiei curente, dar incluzând si factorul aleator. Pentru selectie se foloseste de obicei algoritmul Monte Carlo descris în continuare.

Fie P= si S=. Fie s_i= probabilitatea de selectie a cromozomului p_i. Deci s₁+...+s_n=1. Mai consideram valoarea s₀=0. De n ori procedam astfel:

generam un numar aleator x în intervalul

este selectat acel cromozom p_i pentru care s₀+...+s_i-1 x<s₀+...+s_i

Cei n cromozomi selectati vor constitui noua populatie dupa etapa de selectie. Se observa ca un cromozom poate fi selectat de mai multe ori si de aceea o populatie este un multiset.

Algoritmul de mai sus mai este numit si algoritmul ruletei, deoarece lucrurile se petrec exact ca la o ruleta împartita în sectoare corespunzatoare cromozomilor, de marimi proportionale cu valorile s₁,...,s_n ; la fiecare rotire (aleatoare) a ruletei se ajunge în dreptul unui cromozom.

Etapa de încrucisare (crossover ) consta în selectarea unei subpopulatii a populatiei curente si recombinarea a câte doi indivizi din subpopulatie. Este folosit un parametru pc numit probabilitatea de încrucisare.

Prin recombinarea (încrucisarea) a doi cromozomi se obtin doi descendenti ce au caracteristici ale ambilor parinti. O modalitate simpla de încrucisare a doi cromozomi este cea cu un punct de taietura, în care din "parintii" :

x=(x₁,...,x_k,x_k+1,...,x_r) si y=(y₁,...,y_k,y_k+1,...,y_r)

se obtin "descendentii":

x'=(y₁,...,y_k,x_k+1,...,x_r) si y'=(x₁,...,x_k,y_k+1,...,y_r)

unde k este ales aleator din secventa 1..r-1

În etapa de încrucisare extragem mai întâi o subpopulatie Q a lui P, apoi încrucisam câte doi indivizi din Q, dupa care adaugam noul Q lui P

Q

for i=1,n

x random([0,1))

if x<pc

then P P \ ; Q Q

alegem aleator perechi de elemente din Q si le încrucisam

(daca │Q│ nu este par, un element ramâne neschimbat)

P P Q

Exista o mare varietate de modalitati de încrucisare a doi indivizi. Ne marginim la cele ce folosesc puncte de taietura. Consideram cromozomii:

Daca vom folosi doua puncte de taietura vor rezulta descendentii:

iar daca vom folosi trei puncte de taietura vom obtine descendentii:

cu precizarea ca punctele de taietura sunt alese aleator.

Etapa de mutatie consta în selectarea unei subpopulatii a populatiei curente si aplicarea unor mici perturbari cromozomilor din aceasta subpopulatie. Este folosit un parametru pm numit probabilitatea de mutatie.

O modalitate simpla de mutatie a unui cromozom consta în alegerea aleatoare a unei pozitii din cromozom si modificarea ei: 0↔1.

În etapa de mutatie extragem mai întâi o subpopulatie Q a lui P, apoi aplicam mutatia fiecarui cromozom din Q, dupa care adaugam noul Q lui P

Q

for i=1,n

x random([0,1))

if k<pc

then P P \ ; Q Q

pentru fiecare q Q aplicam operatorul de mutatie

P P Q

Observatii

de obicei pc este de ordinul 10^-1 (de exemplu 0.3), iar pm de ordinul 10^-3 (de exemplu 0.007). Experientele arata ca alegerea lui pc si pm nu are foarte mare importanta. Alegerea lor se face si în functie de lungimea r a cromozomilor;

de regula, în etapa de selectie, cel mai performant individ este retinut si pentru viitoarea configuratie;

în functia de evaluare (dar nu numai) pot fi folosite distante ca de exemplu:

cea euclidiana;

Hamming - numarul de pozitii pe care cromozomii difera;

Levenstein - numarul minim de stergeri + adaugari + modificari pentru

a trece de la un cromozom la celalalt.

Aplicatii

Ghicirea interactiva a unei submultimi p₀ a lui . Inter-activitatea consta în faptul ca pentru fiecare submultime p "calculatorul" întoarce numarul de pozitii pe care p si p₀ coincid.

O submultime a lui poate fi reprezentata ca un vector x ^r cu semnificatia ca i face parte din submultime daca si numai daca x_i=1

Programul a fost rulat pentru n=r=25 pc=0.3, pn=0.2

J(p) = numarul de pozitii pe care p coincide cu p₀ cautata.

Variante folosite pentru încrucisare:

cea clasica;

selectam doi indici p₁<p₂ si interschimbam portiunile corespunzatoare din cromozomi.

Ne oprim daca J(p)≥n-2. Determinarea solutiei exacte poate fi realizata apoi încercând variantele posibile.

Ghicirea unei permutari (interactiv)

Programul a fost rulat pentru n=10 r=10 pc=0.3

Functia J si variantele de crossover sunt aceleasi ca în exemplul precedent.

Mutatia aplicata unui cromozom p consta în a determina aleator indicii j,k si a interschimba p[j] cu p[k]

Maximul unei functii

Dorim sa determinam valoarea x₀ care maximizeaza functia f:[a,b] R. Pentru x₀ sunt cerute k cifre zecimale.

Fie r cel mai mic numar natural cu (b-a)10^k 2^r. Atunci vom lucra cu cromozomi c=(c₁,c₂,...,c_r) de lungime r, unde fiecare c_i . Valoarea x [a,b] corespunzatoare lui c se calculeaza astfel:

fie x' numarul zecimal egal cu (c_rc_r-1...c₂c₁)₂

x=a+x'

Programul a fost rulat pentru n=30 r=20 pc=0.25 pm=0.1

Variante folosite pentru crossover:

cea clasica;

modificam ultimele k pozitii aleator;

selectam doi indici p₁<p₂ si interschimbam portiunile corespunzatoare secventei de indici p₁..p₂

Principiul lui Dirichlet

Prezentam în acest subcapitol un principiu simplu, cu multe aplicatii, dar care nu are generalitatea algoritmilor probabilisti si genetici, studiati anterior.

Principiul lui Dirichlet are un enunt simplu si care nu necesita demonstratie:

	Daca m>k n obiecte sunt plasate în n casute, atunci va exista o casuta ce va contine mai mult de k obiecte.

Prezentam în continuare câteva aplicatii ale acestui principiu.

Exemplul 1. Exista un numar de n perechi de pantofi de marimi diferite, dar nearanjati pe perechi. Care este numarul minim de pantofi care trebuie cercetati pentru a forma o pereche ?

Raspunsul este imediat. Folosim câte o cutie (initial goala) pentru fiecare marime. Este evident ca dupa asezarea în cutii a n+1 pantofi, o cutie va contine doi pantofi (m=n+1 k=1

Exemplul 2. Se considera un vector a=(a₁,...,a_n) de numere naturale. Se cauta indicii i<j cu a_i+...+a_j multiplu de n

În continuare, pentru orice numar natural x, vom nota prin x clasa sa de echivalenta modulo n

Consideram sumele s_k=a₁+...+a_k pentru k=1,...,n. Fie s_k clasele de echivalenta corespunzatoare.

Deosebim doua situatii:

daca exista k cu s_k , atunci o solutie este (i,j)=(1,k)

în caz contrar, este clar ca s₁,...,s_n . Conform principiului lui Dirichlet, vor exista indicii k<l cu s_k=s_l. Atunci o solutie este (i,j)=(k+1,l)

Exemplul 3. Pentru un numar natural n dat, se cauta un multiplu N al sau în a carei scriere obisnuita (în baza 10) apar numai cifrele si

Problema este asemanatoare celei precedente.

Pentru k=1,...,n consideram numarul s_k a carui scriere în baza 10 este formata din k de , adica s₁=1 s₂=11 etc.; fie s_k clasa de echivalenta modulo n corespunzatoare.

La fel ca mai sus, deosebim doua situatii:

daca exista k cu s_k , atunci o solutie este chiar s_k

în caz contrar, este clar ca s₁,...,s_n . Conform principiului lui Dirichlet, vor exista indicii k<l cu s_k=s_l. Atunci o solutie este s_l-s_k, adica numarul în a carei scriere apar l-k de urmati de k de

Exemplul 4. Teorema lui Erdös.

Se dau (m-1)(n-1)+1 numere naturale oarecare. Sa se arate ca printre ele exista m care se divid unul pe altul, sau exista n care nu se divid între ele.

Vom aplica tot principiul lui Dirichlet, dar în plan.

Se ordoneaza mai întâi crescator numerele date.

Consideram un caroiaj cu n-1 linii si m-1 coloane. Vom presupune ca exista si linia imaginara cu numarul de ordine 0, pe care este plasat numarul 1.

Consideram pe rând numerele (în ordine crescatoare). Fiecare numar va fi plasat pe linia i cu i maxim si cu proprietatea ca numarul curent se divide cu un numar aflat pe linia anterioara.

Pentru exemplificare, sa consideram ca n=4 si m=5, iar numerele sunt:

x

Dupa plasarea primelor 8 numere, suntem în situatia:

Daca de exemplu x=72, atunci el ar trebui plasat pe a patra linie (inexistenta) si am obtine n=4 numere care se divid unul pe altul (de exemplu 3, 12, 24, 72).

Daca de exemplu x=35, atunci el ar trebui plasat pe a doua linie si am obtine m=5 numere care nu se divid între ele: 9, 12, 15, 33, 35.

Este important de notat ca pe fiecare linie numerele plasate apar în ordine crescatoare. Principiul lui Dirichlet ne asigura ca cel mai târziu dupa plasarea ultimului numar vom iesi din "cutie": aici caroiajul (n-1)×(m-1)

O varianta a principiului lui Dirichlet este urmatoarea:

	Fie k1,...kn K=(k1+...+kn)/n si x un numar oarecare. Atunci: daca x<K i cu x<ki daca x>K i cu x>ki

Exemplul 5. Daca vârfurile unui decagon sunt etichetate distinct cu numerele 0,1,...,9 într-o ordine oarecare, atunci exista trei vârfuri consecutive pentru care suma etichetelor este mai mare decât 13.

Fie x_i eticheta vârfului i, pentru i=1,...,10. Consideram numerele:

k₁=x₁+x₂+x₃

k₂=x₂+x₃+x₄

. . . .

k₉=x₉+x₁₀+x₁

k₁₀=x₁₀+x₁+x₂

Atunci K=(k₁+...+k_n)/n

Conform principiului lui Dirichlet, va exista i cu k_i>13,5>13.

Exemplul 6. Se considera m calculatoare si n imprimante (m>n). Fie a=numarul minim de legaturi calculator imprimanta ce trebuie stabilite, astfel încât daca orice n calculatoare doresc sa scrie simultan, acest lucru sa fie este posibil. Se cere sa se arate ca a n(m-n+1)

Fie k_i numarul de calculatoare legate la imprimanta i. Numarul de legaturi este deci a=k₁+...+k_n

Daca a<n(m-n+1), atunci (k₁+...+k_n)/n<m-n+1 Conform variantei principiului lui Dirichlet, exista o imprimanta i legata la cel mult m-n calculatoare, deci care nu este legata la cel putin n calculatoare; daca acestea vor sa scrie simultan, nu vor reusi. Contradictie.

Exercitiu. Sa se descrie o modalitate prin care problema poate fi rezolvata cu exact n(m-n+1) legaturi.