BAZELE LOGICE ALE CALCULATOARELOR NUMERICE
Algebra booleana sau algebra logicii este o metoda simbolica pentru studierea relatiilor logice. Bazele algebrei logice au fost puse de matematicianul englez George Boole īn anul 1854.
Algebra booleana si-a gasit o la 343j97d rga aplicare īn domeniul calculatoarelor electronice, datorita faptului ca acestea folosesc elemente fizice care comporta doua stari distincte si lucreaza cu semnale care reprezinta doua valori, denumite semnale binare, valori care pot fi puse īn corespondenta directa cu propozitii logice carora li se asociaza valoarea de fals sau adevarat. Algebra booleana si-a gasit o la 343j97d rga aplicabilitate īn analiza si sinteza schemelor componente si blocurilor functionale ale calculatoarelor numerice.
Algebra booleana este construita pe o multime cu doua valori, utilizata la analiza propozitiilor carora li se asociaza valoarea de fals sau adevarat, cu aplicatie īn domeniul circuitelor de comutatie, unde cele doua valori sunt asociate la doua nivele de potential care pot schimba starea circuitului de comutatie.
Algebra logica lucreaza cu propozitii reprezentānd afirmatii despre care se poate spune ca sunt fie adevarate (unei propozitii adevarate asociindu-se valoarea 1), fie false (unei propozitii false asociindu-se valoarea 0).
O propozitie nu poate fi simultan si adevarata si falsa, astfel putāndu-se introduce o variabila binara, care ia numai valorile 0 sau 1.
Multimea nevida formata din elementele 0,1 o notam cu B = . Asupra ei pot fi aplicate urmatoarele operatii:
- adunare booleana "+" (sau "
- produs Boolean " " (sau "
- complementare "-" (sau "non").
Cu ajutorul variabilelor binare x B B se pot construi functii logice, ca de exemplu:
f : B B functie de o singura variabila
f:
B1 x ...x Bn B![]() functie de n variabile
functie de n variabile
![]() 0 (propozitie falsa)
0 (propozitie falsa)
f( X)
1 (propozitie adevarata)
![]() 0 (propozitie falsa)
0 (propozitie falsa)
f(xl,x2,...xn)
1 (propozitie adevarata)
Functiile de mai multe variabile binare se obtin ca rezultatul reuniunii unor propozitii prin intermediul unor legaturi logice de tipul conjunctiei, disjunctiei, negatiei etc., pentru care algebra logica foloseste metoda simbolica, astfel: " " / "+" pentru disjunctie; ; "-"/ " " pentru conjunctie; "-"/ "-" pentru negatie.
Functiile logice se pot reprezenta sub forma unor expresii sau sub forma tabelelor de adevar, care contin valorile variabilelor īn toate combinatiile posibile si valori corespunzatoare ale functiei dependente.
Legile de compozitie , si legea de negatie pot fi puse īn evidenta cu ajutorul urmatoarelor functii logice:
x, y Bf(x,y) = x y
x, y Bf(x,y) = x y
x Bf(x) = ![]()
Aceste functii pot fi evidentiate si cu ajutorul tabelelor de adevar sau cu ajutorul simbolurilor utilizate pentru reprezentarea cu blocuri elementare.
Tabelul Disjunctie, conjunctie, negatie
|
x |
y |
x y |
x |
y |
x y |
x |
|
||
|
|
Reprezentarea operatiilor logice prin blocuri elementare
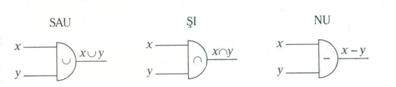
Teoremele fundamentale ale algebrei booleene
La baza algebrei booleene stau urmatoarele teoreme fundamentale:
1. Teoremele de unicitate:
- elementul 1 este unic;
- elementul 0 este unic.
2. Teoremele reuniunii si intersectiei:
a) exista un element 0, numit prim element, cu proprietatile:
x x 0 = 0; x 0 = x
b) exista un element 1, numit ultim element, cu proprietatile:
x x 1 = x; x
3. Teoremele complementarii:
a)
principiul contradictiei: x ![]() = 0
= 0
b)
principiul tertului exclus: x ![]() = 1
= 1
4. Teorema dublei negatii:
![]() = x
= x
5. Teoremele lui De Morgan:
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
6. Teoremele absorbtiei:
x![]()
x![]()
7. Teoremele de idempotenta:
![]()
x![]()
8.
Teoremele de comutativitate, asociativitate si distributivitate
pentru cele 2 legi de compozitie (![]() ,
, ![]() ).
).
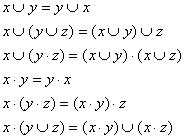
Toate teoremele pot fi interpretate cu ajutorul Diagramelor lui Venn si a tabelelor de adevar.
De exemplu prima teorema a lui De Morgan poate fi demonstrata astfel:

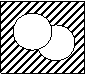

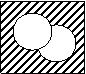

|
X |
y |
|
|
|
|
|
=
|