Backtracking generalizat in plan - Problema labirintului

Metoda Backtracking

Introducere

Metoda backtracking foloseste la rezolvarea multor probleme. Pentru ca o problema sa poata sa fie rezolvata cu metoda backtracking, ea trebuie sa indeplineasca simultan urmatoarele conditii:

- poate avea mai multe solutii, acestea fiind puse sub forma de vector ca de exemplu S(x₁,x₂,x₃,x_n), unde x₁ЄA₁, x₂ЄA₂,, x_nЄA_n

- multimile A₁, A₂, A₃, , An sunt multimi finite, avand elementele aflate intr-o ordine bine stabilita, ele putand sa fie chiar identice.

In acest caz, vectorul care contine solutii se numeste stiva.

Descrierea metodei

Se alege primul element x₁ din A₁. Se repeta intr-o structura repetitiva pana cand nu mai exista elemente netestate din multimea A₁;

- se presupune ca am ajuns la elementul x_k din multimea A_k si se doreste gasirea unui element x_k+1 din multimea A_k+1. Acesta trebuie sa indeplineasca conditiile de existenta a unui astfel de element, impuse de problema, iar daca:

- indeplineste aceste conditii atunci trebuie sa indeplineasca alte conditii impuse de problema, prin care se determina daca el ar putea face parte din solutie. Daca:

- da, atunci se testeaza daca sirul de elemente este o solutie a problemei. Daca:

- da, atunci se tipareste vectorul care contine aceste solutii;

- nu, atunci se trece pe urmatorul nivel din sir (k:=k+1);

- nu, nu indeplineste conditiile de a face parte din solutie, atunci se trece la urmatorul element netestat din multimea A_k;

- nu mai poate exista un element pe nivelul k, atunci se trece la nivelul anterior si se incearca aici gasirea unui element;

- repetitia se termina cand am ajuns pe nivelul 0.

Backtraking generalizat in plan

Metoda Backtracking in plan are cateva modificari:

- stiva contine mai multe coloane (este dubla, tripla, );

- trebuiesc codificate oarecum directiile prin numere, litere, elemente, etc.

Problema labirintului se poate rezolva dupa un algoritm de backtracking generalizat in plan. Ea va fi prezentata in continuare.

Problema labirintului. Enunt: Se da un labirint sub forma de matrice de m linii si n coloane. Fiecare element al matricii reprezinta o camera. Intr-una din camerele labirintului se gaseste un om. Se cere sa se afle toate solutiile ca acel om sa iasa din labirint, fara sa treaca de doua ori prin aceeasi camera.

Generalizare. Aceasta varianta a problemei este varianta in care fiecare camera are peretii proprii in partile laterale. Exista o alta varianta in care fiecare element al matricii este fie un culoar, fie un perete, putandu-se trece doar dintr-un culoar in altul. Aici, se poate trece dintr-o camera in alta, doar daca intre cele doua camere nu exista perete (camerele sunt imediat apropiate). Prin labirint, putem trece dintr-o camera in alta doar mergand in sus, in jos, la stanga sau la dreapta, nu si in diagonala.

Codificare. Principiul backtracking generalizat spune ca trebuies codificate directiile. In aceste caz vor fi codificate si combinatiile de pereti ai fiecarei camere. Asftel, un element al camerei va fi un element al unei matrici cu n linii si n coloane, avand valori de la 0 la 15. In sistemul binar, numerele 0..15 sunt reprezentate ca 0..1111, fiind memorate pe 4 biti consecutivi. Vom lua in cosiderare toti cei 4 biti, astfel numerele vor fi 0000..1111. Fiecare din cei 4 biti reprezinta o directie, iar valoarea lui ne spune daca in acea directie a camerei exista sau nu un perete. Vom reprezenta numarul astfel:

nr = b1 b2 b3 b4(b = bit)

Asftel, b1 indica directia nord (sus), b2 indica directia est (dreapta), b3 indica directia sud (jos) iar b4 indica directia vest (stanga).

Valorile unui bit sunt, fireste, 0 si 1. 0 inseamna ca in directia respectiva nu exista un perete, iar 1 inseamna ca in directia respectiva exista un perete si pe acolo nu se poate trece. De exemplu: 0111 - camera aceasta are pereti in dreapta, in jos si in stanga, iar in sus este drum liber spre camera vecina. Acest numar este de fapt 7, asa fiind notat in matricea labirintului.

In ceea ce priveste directiile, vom retine doar coordonatele unde se afla omul din labirint, acestea fiind schimbate in functie de drumul pe care-l urmeaza. Vom avea o stiva tripla astfel:

- coloana 1 va indica directia. Aceasta va fi de la 1 la 4, 1 reprezentand sus, 2 reprezentand dreapta, 3 reprezentand jos, iar 4, stanga.

- coloana 2 va retine indicele de linie al camerelor parcurse in labirint

- coloane 3 va retine indicele de coloana al camerelor parcurse in labirint

- fiecare linie va insemna o camera, cu indicele de linie si de coloana

Astfel, in cazul in care directia este 1 (sus), linia se va micsora cu 1, daca directia este 2 (dreapta), coloana se va mari cu 1, daca directia este 3 (jos), linia se va mari cu 1, iar daca directia este 4 (stanga), coloana se va micsora cu 1.

Exemplu: Sa presupunem ca introducem urmatoarea matrice:

5 7 5 13

3 8 0 4

14 5 5 7

11 2 6 15

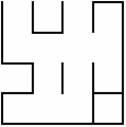
Aceasta matrice corespunde labirintului din desen:

Punctul de pornire din acest labirint este linia 3, coloana 4. Astfel, avea 3 solutii de a iesi din labirint, fara a trece de doua ori prin aceeasi camera:

(3,4)-(2,4)-(2,3)-(1,3)-iesire

(3,4)-(2,4)-(2,3)-(2,2)-(2,1)-(1,1)-iesire

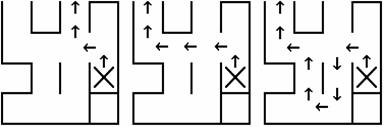
(3,4)-(2,4)-(2,3)-(3,3)-(4,3)-(4,2)-(3,2)-(2,2)-(2,1)-(1,1)-iesire

Rezolvare. Dupa metoda backtracking, trebuiesc gasite toate posibilitatile de a iesi din labirint. S-a iesit din labirint cand linia este 0, coloana este 0, linia este m+1 sau cand coloana este n+1. Trebuie sa trecem din camera in camera, sa verificam toate posibilitatile de iesire.

Cand trecem dintr-o camera in alta, retinem in matricea tripla, directia, linia si coloana respectiva. Va trebui sa respectam regulile preoblemei, adica sa nu trecem de doua ori prin aceeasi camera. Aceasta regula a fost impusa deoarece daca am rezolva problema fara ea, atunci ne-am invarti in gol ! Aceasta verificare se face comparand coordonatele camerei in care suntem cu coordonatele camerelor prin care am trecut, cele retinute de matricea tripla pe coloanele 2 si 3.

Pentru a verifica daca intre doua camere exisa sau nu un perete, va trebui sa respectam un lucru: daca o camera are perete in sus, atunci obligatoriu si camera de sus trebuie sa aiba perete jos, iar daca o camera nu are perete sus, atunci nici camera de sus nu trebuie sa aiba perete jos. Aceasta deoarece daca ar fi asa, am trece dintr-o camera in alta, dar invers nu, ceea ce este imposibil. Imaginati-va ca sunteti intr-o camera. Vreti sa iesiti in hol. Din camera se vede holul si usa, dar dupa ce iesiti in hol si vreti sa reveniti in camera, va intoarce-ti si constatati ca in spatele vostru nu exista nici o usa pentru a intra inapoi in camera, in locul ei fiind doar un perete. Astfel vom verifica dupa relatiile:

a st[k,2],st[k,3]] and 8 = 0       - nu putem merge in sus

a st[k,2],st[k,3]] and 4 = 0       - nu putem merge la dreapta

a st[k,2],st[k,3]] and 2 = 0       - nu putem merge in jos

a st[k,2],st[k,3]] and 1 = 0       - nu putem merge la stanga

a – matricea labirintului st – stiva tripla

Operatorul logic AND verifica bitii corepunzatori ai 2 numere intregi, returnand 1 daca ambii sunt 1 si 0 in rest. Acesta este rezultatul final. 8 inseamna 1000, adica daca camera respectiva are perete sus, rezultatul va fi tot 8, daca nu, va fi 0.

Cand mergem prin labirint, inaintam in camera respectiva iar apoi verificam daca intre cele doua camere exista sau nu perete pentru a putea trece pe acolo. Apoi verificam sa nu fi iesit din labirint ( l₁<1 or l₁>m or c₁<1 or c₁>n ) si daca prin aceasta camera am mai trecut odata.

Afisare. Cand am gasit o solutie, afisam pe rand toate liniile din matricea tripla, dar fara coloana 1, ci numai coloanele 2 si 3.

In continuare, programul care rezolva problema labirintului.

Program labirint;

type stiva=array[1..100,1..3] of integer;

var st:stiva;

m,n,k,i,j,l,c,l1,c1:integer;

as,ev:boolean;

a:array[1..100,1..100] of integer;

procedure init(var st:stiva;k:integer);

begin

st[k,1]:=0;

if k=1 then begin

st[k,2]:=l;st[k,3]:=c;

end else begin

st[k,2]:=l1;st[k,3]:=c1;

end;

end

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k,1]<4 then begin

st[k,1]:=st[k,1]+1;

as:=true;

end else as:=false;

end

procedure valid(var ev:boolean;st:stiva;k:integer);

begin

l1:=st[k,2];c1:=st[k,3];

case st[k,1] of

1: l1:=l1-1;

2: c1:=c1+1;

3: l1:=l1+1;

4: c1:=c1-1;

end;

ev:=true;

case st[k,1] of

1: if a[st[k,2],st[k,3]] and 8<>0 then ev:=false;

2: if a[st[k,2],st[k,3]] and 4<>0 then ev:=false;

3: if a[st[k,2],st[k,3]] and 2<>0 then ev:=false;

4: if a[st[k,2],st[k,3]] and 1<>0 then ev:=false;

end;

for i:=1 to k-1 do if (l1=st[i,2]) and (c1=st[i,3]) then ev:=false;

end

function solutie(k:integer):boolean;

begin

solutie:=(l1<1) or (l1>m) or (c1<1) or (c1>n);

end

procedure tipar;

for i:=1 to k do write(st[i,2],‘ ‘,st[i,3],‘ ‘);

writeln;

end

begin

write('m,n:');readln(m,n);

for i:=1 to m do

for j:=1 to n do read(a[i,j]);

write('l,c:');readln(l,c);

k:=1;init(st,k);

while k>0 do begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar else begin

k:=k+1;

init(st,k);

end else k:=k-1;

end

end