CIRCUITE LOGICE

Calculatorul numeric este compus dintr-un numar foarte mare de componente electronice care alcatuiesc circuitele logice denumite elemente logice sau porti. Aceste porti sunt modele fizice ale unor functii booleene de una sau mai multe variabile.

Indiferent de elementele constructive prin care se realizeaza, un circuit logic se reprezinta ca un bloc cu 929e42j n intrari si una sau doua iesiri. Fiecare iesire reprezinta o functie a celor n variabile de intrare:

Y₁ = f₁ (x₁, x₂, ...x_n);

Y₂ = f₂ (x₁, x₂, ...x_n).

Schema bloc a unui astfel de circuit este reprezentata în figura:

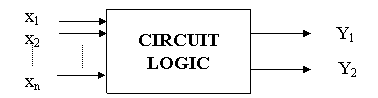
Atât intrarile cât si iesirile sunt marimi ce fac parte din multimea binara B = si se materializeaza prin prezenta unor impulsuri de tensiune sau curent. Functiile f₁ si f₂ se numesc functii de raspuns sau functii de transfer ale circuitului. Din cele expuse mai sus rezulta ca, într-un circuit logic, fiecarei variabile binare (0 sau 1) trebuie sa-i corespunda un nivel de semnal (tensiune sau curent) asociat.

Asocierea se poate face în doua moduri:

cifra 1 binar se exprima prin nivelul de semnal mai mare în valoare algebrica, iar cifra 0 binar se exprima prin nivelul de semnal mai mic în valoare algebrica. Aceasta asociere se numeste logica pozitiva;

cifra 1 binar se exprima prin nivelul de semnal mai mic în valoare algebrica, iar cifra 0 binar se exprima prin nivelul de semnal mai mare în valoare algebrica. Aceasta asociere se numeste logica negativa.

În figura de mai jos sunt reprezentate cifrele binare prin niveluri de tensiune în logica pozitiva:

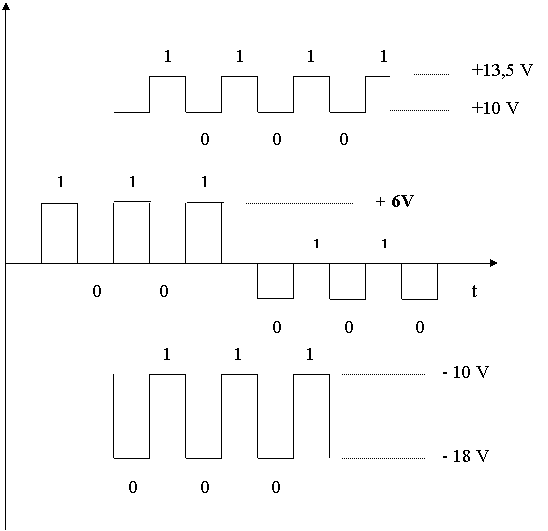
Se observa ca 1 se poate reprezenta prin tensiuni pozitive, negative sau nule. Întotdeauna însa, tensiunea corespunzatoare lui 1 este mai mare în valoare algebrica decât cea corespunzatoare lui 0.

În figura de mai jos sunt reprezentate cifrele binare prin niveluri de tensiune în logica negativa:

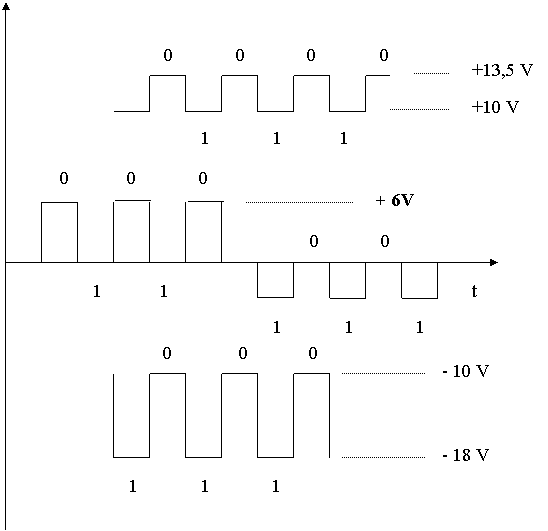
În multe cazuri, datorita avantajelor constructive, una din valorile care exprima pe 0 sau 1, va fi nivelul 0V (masa montajului). Aceasta varianta este reprezentata în figura de mai jos.

În cazul circuitelor integrate, cel mai adesea, nivelele de tensiune ale lui 0 si 1 logic sunt ambele pozitive sau ambele negative, dar în general, unul dintre ele este apropiat de 0V. De asemenea în cazul acestor circuite 1 si 0 logic se exprima printr-o plaja de valori si nu printr-o singura valoare.

Circuitele logice ridica în proiectarea lor, trei probleme importante:

timpul de propagare sau intervalul de timp dintre aplicarea semnalului la intrarea circuitului si aparitia sa la iesire. Acest timp apare datorita regimului tranzitoriu existent în comutarea elementelor de circuit si el trebuie sa fie mai mic decât timpul necesar pentru realizarea oricarei operatii.

numarul de intrari si iesiri ale circuitului care este practic limitat de performantele circuitului,

atenuarea si distorsionarea semnalului, ceea ce face ca identificarea starii binare sa devina imprecisa.

Ultimele doua probleme se pot rezolva prin introducerea unor circuite suplimentare cum ar fi: amplificatoare, circuite de comanda, regeneratoare de nivel etc.

Din punct de vedere al functionarii în timp, circuitele logice se împart în doua categorii:

circuite combinationale,

circuite secventiale.

Circuitele combinationale sunt circuitele pentru care functiile de raspuns, la un moment dat, t₁, nu depind de valorile anterioare, deci nu depind de starea precedenta a circuitului.

Y(t₁) = f (x₁, x₂, ...x_n)

Circuitele combinationale se cunosc si sub denumirea de circuite poarta.

Circuitele secventiale sunt circuite logice pentru care functiile de raspuns la un moment dat, t₁, depind de valorile lor anterioare, la momentul t₀, adica depind de starea precedenta a sistemului.

Y(t ₁) = f x₁, x₂, ...x_n, y (t₀)]

Circuite logice combinationale

Pentru exemplificare vom considera un circuit ce realizeaza functia sI în logica pozitiva cu trei intrari si o iesire, reprezentat în figura de mai jos:

În figura este reprezentata variatia în timp a celor trei semnale de intrare si a semnalului de iesire (functia sI):

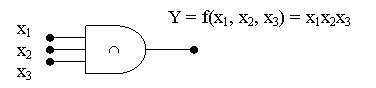
În cazul unui circuit ce realizeaza functia SAU avem urmatoarele reprezentari:

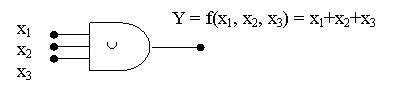
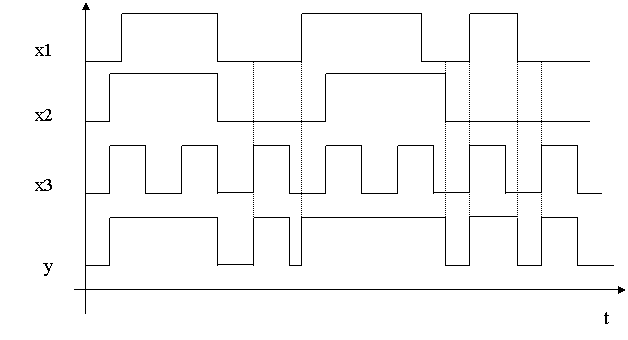
Diagramele de potentiale au fost întocmite pe baza tabelului de adevar de mai jos:

Circuitele combinationale sunt capabile sa realizeze toate functiile booleene de doua sau mai multe variabile. Trebuie retinut faptul ca un circuit logic, în acelasi regim de functionare, realizeaza doua functii booleene diferite, dupa cum s-a asociat logica pozitiva sau logica negativa. De asemenea, exista cazuri când, aceeasi functie booleana se realizeaza de catre doua circuite diferite, unul lucrând în logica pozitiva, iar celalalt în logica negativa.

Dupa tipul componentelor electronice cu care se realizeaza circuitul electric specializat, portile logice pot fi:

cu relee,

cu diode si rezistente,

cu tranzistoare si rezistente,

cu diode, tranzistoare si rezistente,

cu componente integrate.

Exemplu: Circuite sI/SAU cu diode si rezistente, în logica pozitiva, pentru doua intrari.

Circuit de tip sI Circuit de tip SAU

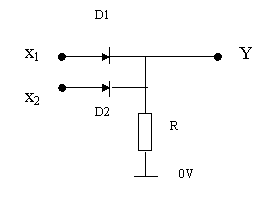
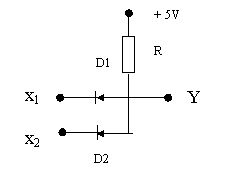
Circuite logice secventiale

Un circuit secvential se caracterizeaza prin aceea ca valoarea functiei de iesire, la un moment dat, depinde atât de valoarea variabilelor de intrare, cât si de valoarea pe care a avut-o functia la momentul precedent. În circuitele secventiale se foloseste mai mult comanda prin semnale (tensiune sau curent), sub forma de impulsuri si mai putin cea sub forma de niveluri.

Ca exemplu, vom considera un circuit diferentiator RC, care transforma fronturile pozitive sau negative ale unui semnal de niveluri în impulsuri exponentiale. Daca se introduce si o dioda, se obtine un singur impuls exponential, ceea ce face ca semnalul de niveluri sa actioneze numai la un anumit front al sau (crescator sau descrescator).

Un circuit RC este reprezentat astfel:

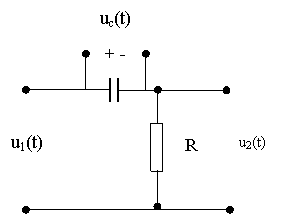
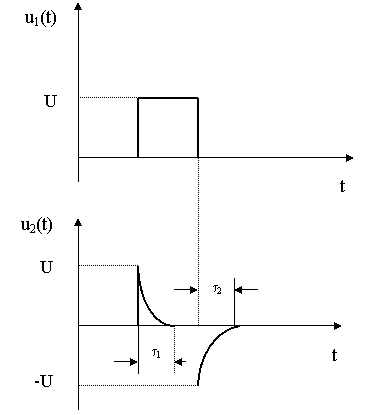
Daca la intrarea circuitului se aplica un impuls dreptunghiular u₁(t) de amplitudine U si durata t, putem scrie u₁(t) = u_c(t) + u₂(t). La aplicarea frontului anterior, condensatorul se comporta la început ca un scurtcircuit, întreaga tensiune de la intrare regasindu-se pe rezistenta R. Odata cu trecerea timpului, condensatorul se încarca, tensiunea u_c(t) crescând exponential la valoarea U, ceea ce face ca tensiunea pe rezistenta, sa scada exponential la zero.

La aparitia frontului posterior al impulsului, condensatorul se afla încarcat la valoarea U, iar tensiunea de intrare u₁(t) devine zero. În acest caz se poate scrie u₂(t) +u_c(t) = 0 sau u₂(t) = -U. La iesire apare deci un impuls de amplitudine -U care scade exponential la zero în intervalul de timp t . Se obtin astfel doua salturi de tensiune foarte scurte, de polaritati opuse, duratele lor fiind de t si t

BLOCURI FUNCŢIONALE

În cadrul unui calculator numeric au loc operatiuni de prelucrare si transfer al informatiei codificata sub forma numerica. Dupa cum s-a aratat, calculatorul se compune din mai multe unitati: memorie, unitati aritmetice, periferice etc. ce îndeplinesc functii distincte si a caror activitate concura la functionarea calculatorului ca un sistem unitar de prelucrare automata a informatiei. La rândul sau, o unitate functionala se compune din mai multe dispozitive sau blocuri functionale.

Un bloc functional reprezinta un ansamblu alcatuit din circuite logice combinationale si secventiale, cu un numar oarecare de intrari si iesiri, si care, prin variatia starilor sale realizeaza o anumita operatie.

În arhitectura unui calculator, acelasi bloc functional intra în componenta mai multor unitati functionale. Printre cele mai reprezentative blocuri functionale elementare se numara: registrele, codificatoare, decodificatoare, numaratoare, selectoare, dispozitive de complementare, dispozitive pentru realizarea operatiilor aritmetice, etc.

Matricea de comutatie

Matricele de comutatie reprezinta o clasa de dispozitive foarte raspândite în calculatoare datorita aplicabilitatii pe care o au. O matrice de comutatie este un circuit logic cu iesiri multiple, care realizeaza o functie matriceala booleana. La o matrice de comutatie iesirile sunt legate de intrari printr-o relatie matriceala. Schema bloc a unei matrice de comutatie este redata mai jos:

Pentru blocul functional din figura, vom considera cele patru iesiri exprimate în functie de intrari sub urmatoarea forma:

A = = m₀ m₂ m₆

B = = m₁ m₂ m₄ m₆ m₇

C = = m₁ m₅

D = = m₀ m₄ m₅

Înlocuind cu minterni vom obtine:

A = (1 m₀ ) m₁ ) m₂ ) m₃ ) m₄ ) m₅ ) m₆ ) m₇)

B = (0 m₀ ) m₁ ) m₂ ) m₃ ) m₄ ) m₅ ) m₆ ) m₇)

C = (0 m₀ ) m₁ ) m₂ ) m₃ ) m₄ ) m₅ ) m₆ ) m₇)

D = (1 m₀ ) m₁ ) m₂ ) m₃ ) m₄ ) m₅ ) m₆ ) m₇)

Din aceasta forma relatiile se pot transpune într-o ecuatie matriciala:

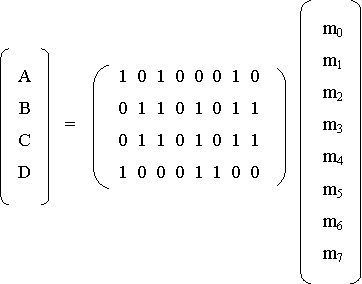
sau prescurtat [E] = [B] [I], adica matricea iesirilor este egala cu matricea intrarilor înmultita cu matricea booleana de transfer.

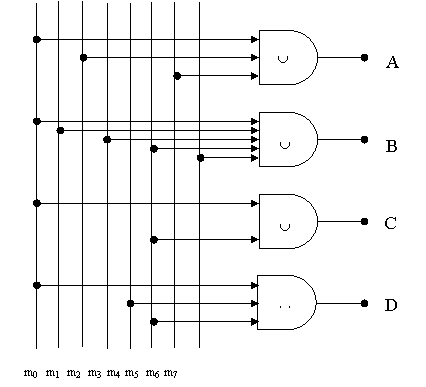Având la dispozitie matricea de intrate m_i si matricea de transfer, schema simbolica cu circuite logice corespunzatoare matricei de comutatie poate fi alcatuita tinând cont ca iesirile reprezinta produsul matriceal între linia corespunzatoare iesirii si vectorul de intrare. De exemplu, la iesirea A se vor lega numai acele intrari carora le corespunde 1 în matricea booleana.

Matricele de comutatie se pot realiza fizic cu diode semiconductoare, tranzistoare, miezuri magnetice toroidale, circuite integrate etc.

În figura de mai jos sunt ilustrate câteva tipuri de matrici de comutatie:

Matricele de decodificare sunt utilizate la conversia numerelor binare în alte sisteme de numeratie, iar cele de codificare la conversia numerelor din alte sisteme de numeratie în binar.

Matricea de selectare are rolul de a selecta o anumita cale din mai multe posibile, iar cea de distributie de a da semnal pe cele 2ⁿ iesiri la un singur semnal primit la intrare.

Principiile care stau la baza realizarii matricelor de comutatie stau si la baza realizarii altor blocuri functionale cum sunt: sumatoarele, numaratoarele etc.