COZI DE PRIORITATE (cu HEAP)

COZI DE PRIORITATE (cu HEAP).

HEAP -ul este o structura de date care memoreaza un arbore binar complet într-un vector. Fiecare nod al arborelui corespunde unui element al vectorului unde se memoreaza valoarea din nod. Arborele este echilibrat, adica numai ultimul nivel este eventual incomplet.

Un vector A care reprezinta un Heap este caracterizat de doua atribute: n=lung(A) care este numarul elementelor memorate în vector si Heap- C lung(A) care este numarul de elemente ale Heap-ului din vectorul A. Deci Heap-Iung(A)~lung(A). Radacina arborelui este întotdeauna A(l) si dându-se un indice i al unui nod, indicii parintelui Par(i) , fii din stânga LS(i) si din dreapta LD(i) pot fi calculati conform algoritmilor :

Functie Par(i) ...

Par = Li/2J

Return

Functie LS(i)

LS = 2*i

Return

Functie LD(i)

LD = 2*i + 1

Return

Pe cele mai multe computere functia LS poate calcula 2*i 151c29b printr-o singura instructiune deplasând catre stânga peste o pozitie binara

reprezentarea binara a lui i. Similar, functia LD poate calcula rapid 2*i + 1 prin deplasare catre stânga peste o pozitie binara reprezentarea lui i si modificând în 1 cel mai din dreapta bit. Functia Par poate calcula i/2 printr-o singura instructiune deplasând catre dreapta peste o pozitie binara reprezentarea binara a lui i.

Reprezentarea unui arbore binar într-un vector oarecare .

Acest arbore este un arbore binar echilibrat si are adâncimea h = log2n. O structura careia i se poate pune în corespondenta un arbore echilibrat se numeste HeapMax daca orice nod are o valoare mai mare decât oricare din fii sai. (Daca orice nod are o valoare mai mica decât oricare dintre fii sai atunci structura se numeste HeapMin ).

Algoritmul de heapificare a unui vector cu n componente începând de la a i-a componenta este:

HEAPIFY(A ,i)

L = 2*i

R = 2*i + 1

Daca L <= Heap-lung(A) si A(L) > A(i) atunci

Imax = L

Altfel

Imax = i

Sdaca

Daca R <= heap-lung(A) si A(R) > A(imax) atunci

Imax=R

Sdaca

Daca Imax I atunci

A(i) A(imax)

Sdaca

Cheama HEAPIFY(A, Imax)

return

Algoritmul pentru constructia unui heap este urmatorul:

CHEAP(A ,n)

Heap-lung(A) = n

pentru i =n/2,1,-1

cheama HEAPIFY (A ,i)

Spentru 

Fisierul al carui arbore atasat este:

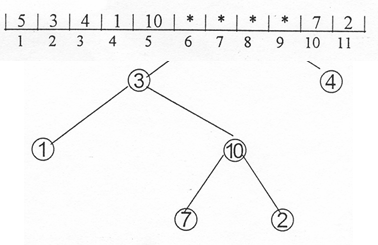
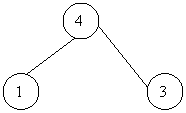
se hipifica în felul urmator:

Pentru I=5

i

i

i

i

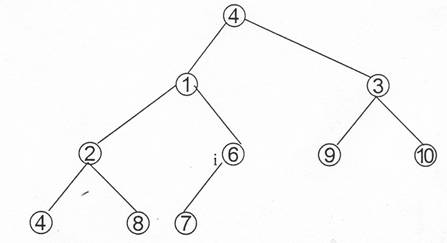
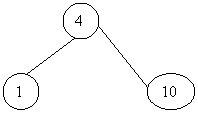
Heap-ul dupa terminarea algoritmului va arata astfel :

Se poate observa ca timpul de executie al lui Heapify depinde de înaltimea nodului în arbore. În heap avem pentru orice înaltime h avem [n/2^h+1] noduri de înaltime h. Cunoscând aceasta putem calcula timpul de executie.

T(n)=S [n/2^h+1]*O(h) = O(n*S [h/2^h+1])= O(n)

^{h=0,lg(n) h=0,lg(n)}

Algoritmul Heapify este de complexitate O(n).

Structura de Heap este foarte utila: am vazut în cursul de 'Algoritmica' ca HeapSort-ul este un excelent algoritm de sortare. În continuare vom prezenta cea mai utilizata aplicatie a unui Heap si anume coada de prioritati.

Coada de prioritati este o structura de date care pastreaza elementele unei multimi S în care fiecarui element îi este asociata o valoare numita prioritate.

7.1 Operatii asupra unei cozi de prioritati:

Introducera unui element x în S Insert(S,x)

Determinarea elementului cu cea mai mare cheie Maxim(S) :

Extragerea elementului cu cea mai mare cheie Extract_Max(S)

Una dintre aplicatiile cozii de prioritati este gestionarea proceselor în programarea partajata. Coada de prioritati pastreaza lista proceselor care trebuie sa fie efectuate si prioritatile acestora. Când un proces s-a încheiat sau s-a întrerupt se introduce un nou proces, alegerea acestuia se face în functie de prioritatea atasata. Deci se va folosi Extract_Max(S) pentru alegerea procesului cu cea mai mare si Insert(S ,x) pentru a-l introduce în lucru. O coada de prioritati poate fi folosita si în simularea conducerii evenimentelor.

În continuare vom prezenta algoritmii care implementeaza cu ajutorul Heap-ului operatiile care se pot efectua asupra unei cozi.

Extract_Max(A,max)

Daca Heap-lung(A) < 1 atunci

EROARE " heap vid"

Sdaca

max = A(l)

A(l) = A(Heap-lung(A) )

Heap-lung(A) = Heap-lung(A) - 1

Cheama Heapify(A,l)

Return

Evident ca, deoarece heapul s-a stricat doar la vârf, Heapify(A,l) va parcurge doar o singura data arborele de la radacina la o frunza, deci complexitatea va fi O(lg n).

Insert(A,cheie)

Heap-lung(A) = Heap-lung(A) + 1

i= Heap-lung(A)

Atât timp cât i> 1 si A(Par(i)) < cheie

A(i) = A(Par(i))

i= Par(i)

A(i) = cheie

Sciclu

Si aceasta procedura va parcurge doar o singura data arborele de la radacina la o frunza, deci complexitatea va fi O(lg n).

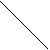
Figura urmatoare ilustreaza operatia Insert asupra heap-ului a) în care urmeaza sa fie inserat un nod cu cheia 15.

a)

Cheia 15 a fost iserata la locul ei.

Puteti observa, pe succesiunea de arbori, ca s-a creat mai întâi locul si apoi, '15' a trecut la locul corect urcând în sus în arbore, din parinte în parinte.

Întrebari si exercitii la capitolul 7.

Exercitiul 1.

Aratati cum se poate implementa o stiva cu ajutorul unui HEAP.

Exercitiul 2.

Aratati cum se poate implementa o coada cu ajutorul unui HEAP.

Exercitiul 3.

Având un arbore binar memorat secvential scrieti algoritmul care listeaza nodurile fara descendent stâng.