Controlul sistemelor de productie

In cursurile 2 si 3 am vazut maniera in care o problema de IA poate fi formalizata. Am discutat despre spatiul starilor unei probleme si am invatat sa alegem o reprezentare pentru stari. Stim ca tranzitiile intre stari 151b14b sint descrise de un set de operatori pe care le-am numit reguli de productie si am vazut ca a rezolva o problema inseamna a gasi un drum intre o stare initiala si una sau mai multe stari finale ce sint cunoscute precis ori numai descrise printr-un set de restrictii. Maniera in care organizam cautarea in spatiul starilor, deci modul in care inlantuim operatorii pentru gasirea solutiei constituie subiectul prezentului curs.

Cautarea solutiei

Problemele de IA se aseamana prin aceea ca toate presupun existenta unei stari initiale cunoscute, a uneia sau mai multe stari finale precizate exact sau prin conditii, iar rezolvarea ei inseamna gasirea unui traseu intre starea initiala si o stare finala. Asadar, de cele mai multe ori, a rezolva o problema de IA inseamna nu a gasi o anume stare, ci a gasi un drum care sa uneasca o stare initiala de una finala.

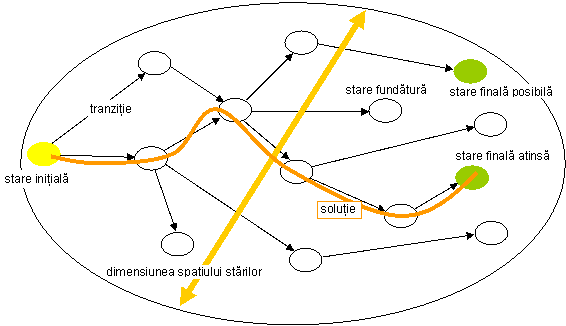
Figura 1: Spatiul starilor in problemele de IA

Acest lucru face ca o problema de IA sa fie una de cautare intr-un spatiu al starilor. In functie de dimensiunea acestui spatiu se utilizeaza diferite metode pentru a eficientiza procesul de navigare. In limbajului domeniul IA, aceste metode se mai numesc si strategii. Exista mai multe tipuri de strategii, dar ele sint clasificate in doua clase mari: irevocabile si tentative. Aplicarea unei strategii este necesara pentru a decide calea de urmat in situatiile in care dintr-o stare anumita exista mai multe cai de a tranzita intr-o alta stare.

Strategii irevocabile

O strategie irevocabila este una in care orice miscare in spatiul starilor este ireversibila. Cale de intoarcere nu exista. O strategie irevocabila aparent merge la sigur. Este ca si cum as cunoaste deja solutia si atunci ma indrept direct spre ea. Imposibilitatea de a mai continua la un moment dat duce, inevitabil, la oprirea cautarii si deci la esec. Dar ce sens mai are cautarea daca cunosc deja solutia? Distinctia provine din gradul de cunoastere a solutiei problemei: cunoastere globala (imaginati-va gasirea drumului intr-un labirint privit dintr-un balon) fata de cunoastere locala (labirintul privit de un om aflat in el). Un sistem de IA care lucreaza cu o strategie irevocabila are o cunoastere locala a problemei, el aplicind o maniera generala de comportament in toate situatiile similare.

Metoda ascensiunii (hill climbing

Numele metodei este dat de analogia cu maniera de catarare pe un deal a unui orb. El nu e capabil a vedea virful dealului unde trebuie sa ajunga dar poate gasi, incercind la fiecare pas in jurul lui cu bastonul, permanent directia care-l face sa urce.

Figura 2: Urcarea dealului (hiil climbing)

procedure hill-climbing(initial-state)

begin

current-state = initial-state;

if (current-state e stare finala) return current-state;

while (mai exista operatori posibil de aplicat lui current-state)

return fail;

end

Iteratia grupului while semnifica aici nu tranzitarea pe rind in starile vecine ci procesul de cautare pentru gasirea primei stari care este "mai sus", adica mai aproape de solutie, fata de cea curenta.

O varianta recursiva a acestui algoritm este urmatoarea:

procedure hill-climbing(current-state)

begin

if (current-state e stare finala) return current-state;

while (mai exista operatori posibil de aplicat lui current-state)

return fail;

end

In ambele variante, prima stare "mai buna" decit cea curenta este aleasa. O alta varianta a manierei de catarare a dealului alege "cea mai buna" stare vecina. Din acest motiv metoda se numeste a gradientului maxim (stiffest gradient

A decide cind o stare este "mai buna" decit alta presupune existenta unui criteriu de comparare a starilor intre ele. Acesta poate fi dat de o functie euristica[1] (sau de evaluare a starii). Deci primul lucru ce trebuie avut in vedere atunci cind se apeleaza la metoda hill-climbing este construirea unei astfel de functii. Acest lucru ne este intotdeauna usor. Vom exemplica aceasta alegere pe un alt exemplu clasic.

Metoda ascensionala cauta sa atinga starea caracterizata de valoarea maxima a functiei euristice. Metoda nu garanteaza gasirea unei solutii din cauza ca anumite probleme pot avea maxime locale sau platouri, dupa cum se sugereaza in Figura 3

Figura 3 : Maximele locale si platourile opresc inaintarea spre solutie

Problema 8-puzzle: Exista o spatiu de joc 3x3, deci asigurind 9 pozitii, in care pot glisa in directia spatiului neocupat 8 piese inscrise cu numere intre 1 si 8. Plecind de la o distributie initiala a pieselor pe tabla se cere aducerea lor intr-o stare finala impusa. Un exemplu de instanta a problemei 8-puzzle este prezentat in Figura 4

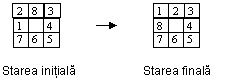
Figura 4 : O instanta a problemei 8-puzzle

Operatori (reguli): muta blanc sus, muta blanc jos, muta blanc dreapta, muta blanc stanga.

Functia euristica: nr. de piese aflate in pozitii finale.

f(stare initiala) = 4; f(stare finala) = 8;

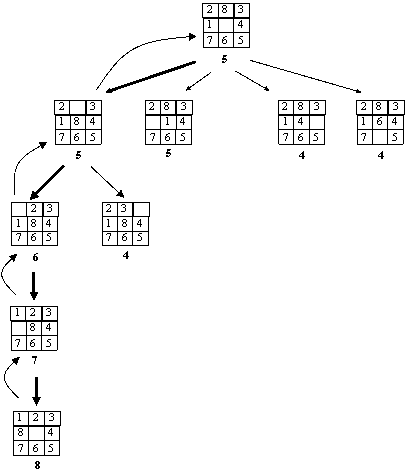
Figura 5: Un exemplu de arbore de cautare pentru problema 8-puzzle

(Sub fiecare stare este notat scorul staii. Avansarea spre

solutie este data de sagetile groase.)

Strategii tentative

O strategie tentativa este una sovaitoare: o miscare ce se dovedeste gresita poate fi indreptata. Miscarea in spatiul starilor nu este inexorabila. Daca s-a ajuns intr-un punct mort pot sa 'iau urma indarat' pentru a face o alta miscare dintr-o pozitie anterioara celei curente, in care am mai fost.

Metoda ascensionala cu revenire (backtracking hill climbing

procedure backtracking-hill-climbing(initial-state)

begin

stack = initial-state;

while (stack) begin

current-state = pop(stack);

if (current-state e stare finala) return current-state;

else begin

evalueaza functia de cost pentru descendentii lui current-state;

elimina dintre aceste stari pe acelea in care am mai fost;

sorteaza starile ramase in ordinea descrescatoare a valorilor functiei de cost;

introdu-le in stiva (push) in aceasta ordine;

end

end

return fail;

end

Se observa ca ordonarea noilor stari gasite se face inainte de introducerea lor in stiva Inseamna ca prima stare ce va fi considerata in continuare este cea din care pot sa ajung cel mai sus din starea in care ma aflu. Daca la un moment dat ajung intr-un punct de maxim local sau de platou, daca stari noi pot fi atinse din starea curenta, ele se introduc in stiva, chiar daca acestea se afla "mai jos" decit starea curenta in drumul spre solutie. Acest lucru permite abordarea altor cai neexplorate si "ocolirea" virfurilor locale sau a platourilor. Interzicerea introducerii in stiva a starilor prin care s-a mai trecut impiedica intrarea in bucle infinite.

Metode de cautare sistematica (brute-force)

Metodele de cautare sistematica investigheaza in totalitate spatiul starilor, plecind din starea initiala, pentru gasirea unei cai catre starea (starile) finala (finale). Aceste metode pot fi aplicate cind spatiul starilor este rezonabil de mic, in asa fel incit sa ne putem permite, in extremis, parcurgerea lui exhaustiva.

Metode de tip genereaza si testeaza

Metodele de tip genereaza si testeaza utilizeaza un generator care furnizeaza o stare urmatoare inca nevizitata. Toata euristica se afla in generator. Acesta poate implementa o lista, o stiva sau o coada si atunci vom recunoaste diferite metode specifice. Procedura generala este urmatoare:

procedure generateAndTest()

while (generatorul nu e gol)

return failure

Cautare intai-in-adincime (depth-first search

In cautarea intii-in-adincime generatorul implementeaza o stiva. Prin aceasta inainte de a cauta in fratii unui nod, intii fiii acestuia sint cautati. Aceasta ordine este dictata de faptul ca, dupa vizitarea unui nod N, intii N este eliminat din stiva si apoi fiii acestuia sint introdusi in stiva. Datorita caracteristicii last-in-first-out ei vor fi parcursi inaintea altor noduri aflate deja acolo. Cind spatiul starilor este un arbore, cautarea intii-in-adincime parcurge arborele cu predilectie in adincime, de unde si numele metodei.

procedure depthFirstSearch(root)

STACK = o stiva continand nodul radacina root;

while (STACK nu e goala)

begin

node = pop(STACK);

if goal(node) then return node;

else push succesorii lui node;

end

return FAIL;

Aceasta procedura testeaza solutia in fiecare nod al arborelui. Daca doar nodurile frunza sunt solutii posibile, procedura se schimba astfel:

procedure leafDepthFirstSearch(root)

STACK = o stiva continand nodul radacina root;

while (STACK nu e goala)

begin

node = pop(STACK);

if not(leaf(node)) push succesorii lui node;

else if goal(node) then return node;

end

return FAIL;

Un dezavantaj al cautarii in adincime il constituie posibilitatea ca algoritmul sa nu se termine in cazul arborilor infiniti. Desigur in practica nu se lucreaza cu arbori infiniti, dar problema ramine pentru ca e inca posibil ca algoritmul sa genereze un numar foarte mare de noduri chiar daca solutia se afla pe un nivel superior, dar pe o ramura aflata in dreapta arborelui.

Cautare intai in largime (breadth-first search

procedure breadthFirstSearch(root)

QUEUE = o coada continand nodul radacina root;

while (QUEUE nu e goala)

begin

node = first(QUEUE);

if goal(node) then return node;

else introdu in spatele cozii succesorii lui node;

end

return FAIL;

O cautare in largime are mai mari sanse sa gaseasca intii nodul solutie aflat pe cel mai inalt nivel, decit o cautare in adincime.

Cautarea cel-mai-bun-intii (best-first)

Metoda de cautare cel-mai-bun-intii (best-first) combina metodele depth-first si breadth-first in sensul ca ia de la prima urmarea unei singure cai o data, iar de la a doua faptul ca nu se impotmoleste in nodurile care nu au urmasi.

Metoda: la fiecare pas sorteaza toate nodurile ce nu au fost inca vizitate in ordinea crescatoare a distantei pina la un nod final si alege pentru expandare in continuare pe cel mai bine plasat.

Ea poate fi aplicata in egala masura parcurgerii arborilor ca si a grafurilor.

Figura 6 prezinta un exemplu de cautare best-first pe un arbore.

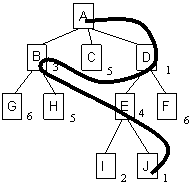
Figura 6 : Un exemplu de cautare best-first

Cifrele de linga noduri in

Figura 6 si cele ce insotesc ca puteri numele de noduri in tabela urmatoare reprezinta costuri.

Pentru transpunerea metodei la o cautare pe grafuri vom folosi doua liste de noduri:

OPEN: noduri care au fost generate si au functia euristica aplicata asupra lor, dar care nu au fost inca vizitate. Elementele in aceasta lista sint intotdeauna sortate in ordinea crescatoare a valorilor functiei euristice.

CLOSED: noduri care au fost deja examinate. O astfel de lista e necesara daca structura este una de graf, iar nu de arbore, intrucit, la fiecare generare a unui nou nod, lista este cautata si nodul generat numai daca el nu exista deja in CLOSED.

Functia euristica f', in multe cazuri, este rezultatul sumei a doua valori:

g - un cost al traversarii grafului din nodul start pina in nodul curent, si

h' - un cost al estimarii traversarii grafului din nodul curent pina intr-un nod final:

f' = g + h'

Un algoritm cunoscut care aplica best-first pentru cautare pe grafuri este A*.